matching_network

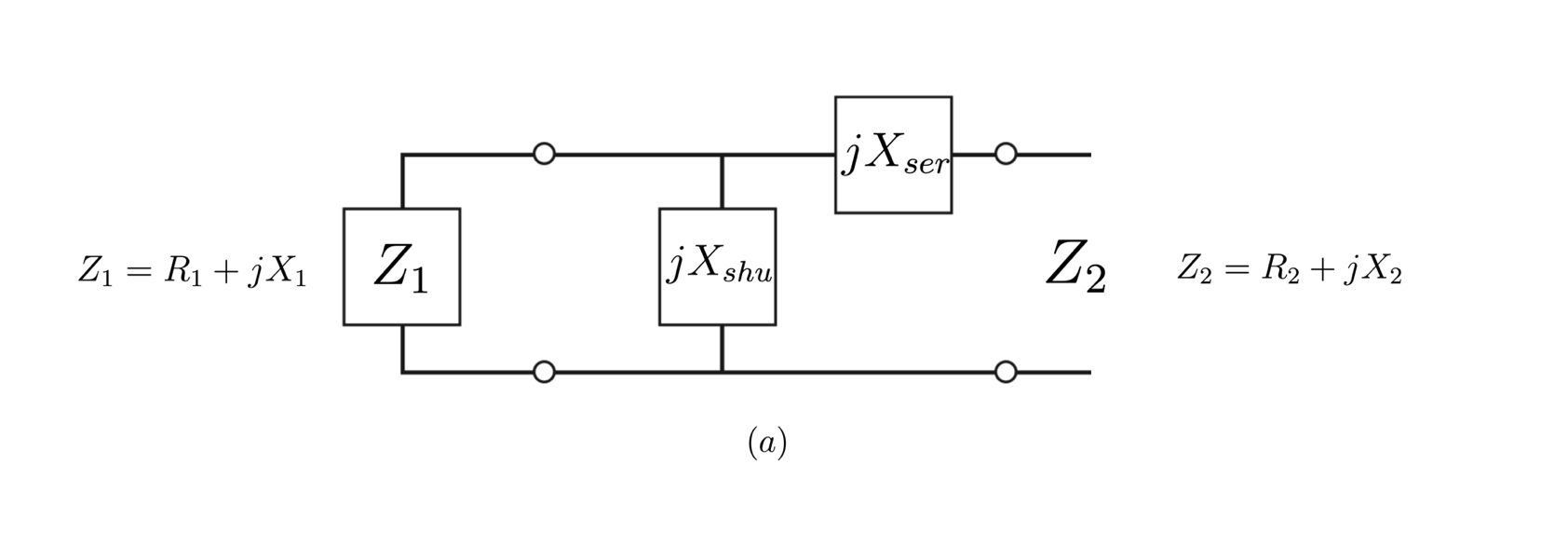
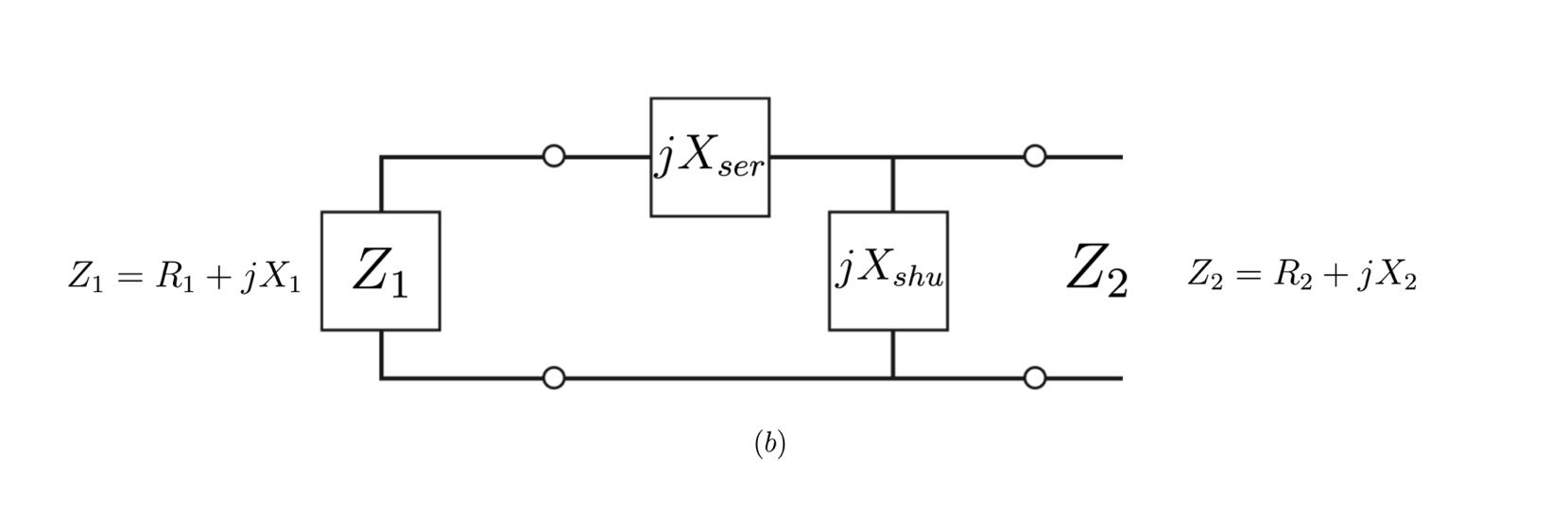
Solve L-section lumped parameters matching networks in a wink. (See How to use section)

Badges

Shunt-series config.

Series-shunt config.

Jupyter Notebooks
L-section_matching_calculations (Initial Jupyter notebook implementation)
Calculations (Matlab pre-calculations)

Installation

pip install matching_network

How to use

From the CLI

matching_network --from 100 --to 20+43j --freq 13.56e6 # both impedances in Ω. 

From (100+0j) Ω to (20+43j) Ω

normalized starting impedance = (100+0j)Ω / (20+43j)Ω = 0.88928-1.912j

#solutions: 4

shunt-series
    Shunt Inductor:
    X = 50 Ω ⇔ B = -20 mS
    L = 586.85 nH  (@ 13.56 MHz)
    Series Inductor:
    X = 3 Ω ⇔ B = -333.33 mS
    L = 35.211 nH  (@ 13.56 MHz)
shunt-series
    Shunt Capacitor:
    X = -50 Ω ⇔ B = 20 mS
    C = 234.74 pF  (@ 13.56 MHz)
    Series Inductor:
    X = 83 Ω ⇔ B = -12.048 mS
    L = 974.18 nH  (@ 13.56 MHz)
series-shunt
    Series Inductor:
    X = 35.285 Ω ⇔ B = -28.341 mS
    L = 414.14 nH  (@ 13.56 MHz)
    Shunt Inductor:
    X = 62.571 Ω ⇔ B = -15.982 mS
    L = 734.4 nH  (@ 13.56 MHz)
series-shunt
    Series Capacitor:
    X = -35.285 Ω ⇔ B = 28.341 mS
    C = 332.64 pF  (@ 13.56 MHz)
    Shunt Inductor:
    X = 44.929 Ω ⇔ B = -22.257 mS
    L = 527.33 nH  (@ 13.56 MHz)

matching_network --from "24.3+8.3j mS"  --to 1.1+9.3j # default in Ω unless specified, using `mS`.

Inside Python

>>> import matching_network as mn
>>>
>>> impedance_you_have         = 90 + 32j # Ω
>>> impedance_you_want_to_have = 175      # Ω
>>>
>>> frequency                  = 900e6    # Hz
>>>
>>> mn.L_section_matching(impedance_you_have, impedance_you_want_to_have, frequency).match()
From (90+32j) Ω to 175 Ω

normalized starting impedance = (90+32j)Ω/175Ω = 0.51429+0.18286j

#solutions: 2

series-shunt
    Series Inductor:
    X = 55.464 Ω ⇔ B = -18.03 mS
    L = 9.8082 nH  (@ 900 MHz)
    Shunt Capacitor:
    X = -180.07 Ω ⇔ B = 5.5533 mS
    C = 982.04 fF  (@ 900 MHz)

series-shunt
    Series Capacitor:
    X = -119.46 Ω ⇔ B = 8.3707 mS
    C = 1.4803 pF  (@ 900 MHz)
    Shunt Inductor:
    X = 180.07 Ω ⇔ B = -5.5533 mS
    L = 31.844 nH  (@ 900 MHz)

>>>

Francesco Urbani