Instantiating Modules

Module Instantiation

Like other hardware description languages, Chisel allows fairly straightforward module instantiation to enable modularity and hierarchy. In Chisel, instantiating a Module class is the equivalent to instantiating a module in Verilog. To do this, we simply use a call to Module with the module created with the Scala new keyword in order to indicate that we are instantiation a new module. We want to make sure we assign this to a value so that we can reference its input and outputs, which we also need to connect.

For example, suppose we would like to construct a 4-bit adder using multiple copies of the FullAdder module, as shown in the Figure 1.

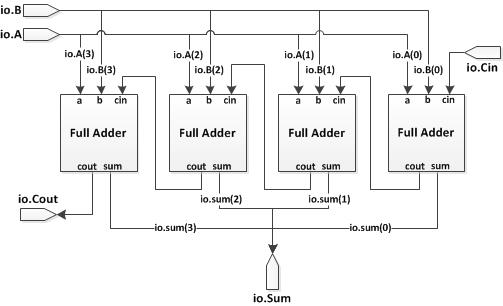
The Chisel source code is shown below.

// A 4-bit adder with carry in and carry out
class Adder4 extends Module {
  val io = IO(new Bundle {
    val A    = Input(UInt(4.W))
    val B    = Input(UInt(4.W))
    val Cin  = Input(UInt(1.W))
    val Sum  = Output(UInt(4.W))
    val Cout = Output(UInt(1.W))
  })
  // Adder for bit 0
  val Adder0 = Module(new FullAdder())
  Adder0.io.a   := io.A(0)
  Adder0.io.b   := io.B(0)
  Adder0.io.cin := io.Cin
  val s0 = Adder0.io.sum
  // Adder for bit 1
  val Adder1 = Module(new FullAdder())
  Adder1.io.a   := io.A(1)
  Adder1.io.b   := io.B(1)
  Adder1.io.cin := Adder0.io.cout
  val s1 = Cat(Adder1.io.sum, s0)
  // Adder for bit 2
  val Adder2 = Module(new FullAdder())
  Adder2.io.a   := io.A(2)
  Adder2.io.b   := io.B(2)
  Adder2.io.cin := Adder1.io.cout
  val s2 = Cat(Adder2.io.sum, s1)
  // Adder for bit 3
  val Adder3 = Module(new FullAdder())
  Adder3.io.a   := io.A(3)
  Adder3.io.b   := io.B(3)
  Adder3.io.cin := Adder2.io.cout
  io.Sum  := Cat(Adder3.io.sum, s2).asUInt
  io.Cout := Adder3.io.cout
}

In this example, notice how when referencing each module I/O we must first reference io that contains the ports for the I/Os. Again, note how all assignments to the module I/Os use a reassignment operator :=. When instantiating modules, it is important to make sure that you connect all the input and output ports. If a port is not connected, the Chisel compiler may optimize away portions of your design that it finds unnecessary due to the unconnected ports and throw errors or warnings.

The Vec Class

The Vec class allows you to create an indexable vector in Chisel which can be filled with any expression that returns a chisel data type. The general syntax for a Vec declaration is given by:

val myVec = Vec(Seq.fill( <number of elements> ) { <data type> })

Where <number of elements> corresponds to how long the vector is and <data type> corresponds to what type of class the vector contains.

For instance, if we wanted to instantiate a 10 entry vector of 5 bit UInt values, we would use:

val ufix5_vec10 := Vec(Seq.fill(10) { UInt(5.W) })

If we want to define a register of vector...

val reg_vec32 = Reg(Vec(Seq.fill(32){ UInt() }))

In order to assign to a particular value of the Vec, we simply assign the target value to the vector at a specified index. For instance, if we wanted to assign a UInt value of zero to the first register in the above example, the assignment would look like:

reg_vec32(0) := 0.U

To access a particular element in the vector at some index, we specify the index of the vector. For example, to extract the 5th element of the register vector in the above example and assign it to some value reg5, the assignment would look like:

val reg5 = reg_vec(5)

The syntax for the Vec class is slightly different when instantiating a vector of modules.When instantiating a vector of modules the data type that is specified in the {} braces is slightly different than the usualy primitive types. To specify a vector of modules, we use the io bundle when specifying the type of the vector. For example, in order to specify a Vec with 16 modules , say FullAdders in this case, we would use the following declaration:

val FullAdders = 
  Vec(Seq.fill(16){ Module(new FullAdder()).io })

Notice we use the keyword new in the vector definition before the module name FullAdder. For how to actually access the io on the vector modules, refer to the next section.

Vec Shift Reg

The next assignment is to construct a simple bit shift register. The following is the template from $TUT_DIR/src/main/scala/problems/VecShiftRegisterSimple.scala:

class VecShiftRegisterSimple extends Module {
  val io = IO(new Bundle {
    val in  = Input(UInt(8.W))
    val out = Output(UInt(8.W))
  })
  val initValues = Seq.fill(4) { 0.U(8.W) }
  val delays = RegInit(VecInit(initValues))
  ...
  io.out := 0.U
}

where out is a four cycle delayed copy of values on in.

Parametrization

In the previous Adder example, we explicitly instantiated four different copies of a FullAdder and wired up the ports. But suppose we want to generalize this structure to an n-bit adder. Like Verilog, Chisel allows you to pass parameters to specify certain aspects of your design. In order to do this, we add a parameter in the Module declaration to our Chisel definition. For a carry ripple adder, we would like to parametrize the width to some integer value n as shown in the following example:

// A n-bit adder with carry in and carry out
class Adder(n: Int) extends Module {
  val io = IO(new Bundle {
    val A    = Input(UInt(n.W))
    val B    = Input(UInt(n.W))
    val Cin  = Input(UInt(1.W))
    val Sum  = Output(UInt(n.W))
    val Cout = Output(UInt(1.W))
  })
  // create a vector of FullAdders
  val FAs = Vec(Seq.fill(n){ Module(new FullAdder()).io })

  // define carry and sum wires
  val carry = Wire(Vec(n+1, UInt(1.W)))
  val sum   = Wire(Vec(n, Bool()))

  // first carry is the top level carry in
  carry(0) := io.Cin

  // wire up the ports of the full adders
  for(i <- 0 until n) {
    FAs(i).a   := io.A(i)
    FAs(i).b   := io.B(i)
    FAs(i).cin := carry(i)
    carry(i+1) := FAs(i).cout
    sum(i)     := FAs(i).sum.toBool()
  }
  io.Sum  := sum.asUInt
  io.Cout := carry(n)
}

Note that in this example, we keep track of the sum output in a Vec of Bools. This is because Chisel does not support bit assignment directly. Thus in order to get the n-bit wide sum in the above example, we use an n-bit wide Vec of Bools and then cast it to a UInt().

You will notice that modules are instantiated in a Vec class which allows us to iterate through each module when assigning the ports connections to each FullAdder. This is similar to the generate statement in Verilog. However, you will see in more advanced tutorials that Chisel can offer more powerful variations.

Instantiating a parametrized module is very similar to instantiating an unparametrized module except that we must provide arguments for the parameter values. For instance, if we wanted to instantiate a 4-bit version of the Adder module we defined above, it would look like:

val adder4 = Module(new Adder(4))

We can also instantiate the Adder by explicitly specifying the value of its parameter n like the this:

val adder4 = Module(new Adder(n = 4))

Explicitly specifying the parameter is useful when you have a module with multiple parameters. Suppose you have a parametrized FIFO module with the following module definition:

class FIFO(width: Int, depth: Int) extends Module {...}

You can explicitly specify the parameter values in any order:

val fifo1 = Module(new FIFO(16, 32))
val fifo2 = Module(new FIFO(width = 16, depth = 32))
val fifo3 = Module(new FIFO(depth = 32, width = 16))

All of the above definitions pass the same parameters to the FIFO module. Notice that when you explicitly assign the parameter values, they can occur in any order you want such as the definition for fifo3.

Built In Primitives

Like other HDL, Chisel provides some very basic primitives. These are constructs that are built in to the Chisel compiler and come for free. The Reg, UInt, and Bundle classes are such primitives that have already been covered. Unlike Module instantiations, primitive do not require explicit connections of their io ports to use. Other useful primitive types include the Mem and Vec classes which will be discussed in a more advanced tutorial. In this tutorial we explore the use of the Mux primitive.

The Mux Class

The Mux primitive is a two input multiplexer. In order to use the Mux we first need to define the expected syntax of the Mux class. As with any two input multiplexer, it takes three inputs and one output. Two of the inputs correspond to the data values A and B that we would like to select which can be any width and data type as long as they are the same. The first input select, which is a Bool type, determines which one to output. A select value of true will output the value A, while a select value of false will pass B.

val out = Mux(select, A, B)

Thus if A=10, B=14, and select was true, the value of out would be assigned 10. Notice how using the Mux primitive type abstracts away the logic structures required if we had wanted to implement the multiplexer explicitly.

Parameterized Width Adder

The next assignment is to construct an adder with a parameterized width and using the built in addition operator +. The following is a the template from $TUT_DIR/src/main/scala/problems/Adder.scala:

class Adder(val w: Int) extends Module {
  val io = IO(new Bundle {
    val in0 = Input(UInt(1.W))
    val in1 = Input(UInt(1.W))
    val out = Output(UInt(1.W))
  })
  ...
  io.out := 0.U
}

where out is sum of w width unsigned inputs in0 and in1.

Notice how val is added to the width parameter value to allow the width to be accessible from the tester as a field of the adder module object.

Edit your copy of $TUT_DIR/src/main/scala/problems/Adder.scala and run:

./run-problem.sh Adder

until your circuit passes the tests.

Prev (Basic Types and Operations) Next (Writing Scala Testbenches)