-
-
Notifications
You must be signed in to change notification settings - Fork 76
User Guide for QUDT
This guide attempts to explain how the QUDT model should be used.
3. Introducing Dimension Vectors (for SI units)
4. Conversion Multipliers in QUDT
6. Using Quantity Kinds with Dimensionless Quantities
7. Special case of Quantity Kind with no Dimension Vector
8. A Quantity with multiple units
Please refer to the following architecture diagram for the key QUDT classes (the QUDT architecture overview can be read here.
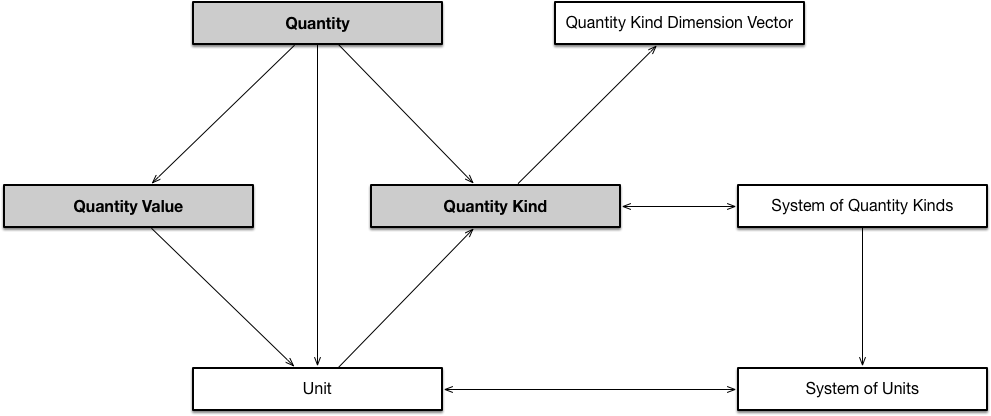
Let's suppose you have a smart thermostat and it generates a digital signal for the temperature setting in degrees Fahrenheit. You could name the QUDT Quantity something like wiki-examples:MyThermostatSetting. The Quantity instance is yours - you can name it whatever you want, but in a professional/interoperability scenario the name might include other information, such as the location of the thermostat. One way or another, the name establishes the context of the value you are storing. For the simple case, the Quantity instance has a property qudt:value, which you could assign the value 72.0. The Quantity instance also points to an instance of qudt:Unit called unit:DEG_F.
Here's the Turtle source code for this:
wiki-examples:MyThermostatSetting
rdf:type qudt:Quantity ;
qudt:hasUnit unit:DEG_F ;
qudt:value "72.0"^^xsd:float ;
.
Here's how it fits into the QUDT model. (Orange is your new instance, blue is defined by QUDT).

The next important concept to understand is the QuantityKind. Simply stated, a QuantityKind is just that: a kind, and answers the question "What is this measurement and unit a measure of?". Answers might be things like "Thermodynamic Temperature" (i.e. quantitykind:ThermodynamicTemperature). So the QuantityKind vocabulary is a set of all the kinds of things we might measure... length, area, electrical capacitance, torque, and really obscure ones like power per area quartic temperature. This last one is measured in units of Watts Per Square Meter Per Quartic Kelvin by the way.
Every Unit is associated with at least one QuantityKind - sometimes more than one if there are different ways people refer to a QuantityKind, but usually just one. You don't need to populate that link, it is already populated. For example, the following SPARQL query produces 2 quantity kinds associated with the unit unit:A-PER-MilliM:
SELECT ?un ?qk
WHERE {
BIND (unit:A-PER-MilliM AS ?arg1) .
?un rdf:type qudt:Unit .
BIND (afn:localname(?un) AS ?unn) .
FILTER (?un = ?arg1) .
?un qudt:hasQuantityKind ?qk
} ORDER BY ?un
which produces the following:
un qk
unit:A-PER-MilliM quantitykind:LinearElectricCurrent
unit:A-PER-MilliM quantitykind:MagneticFieldStrength
Of course, each QuantityKind could be measured in any of several units, such as different units for temperature, or different units for length. For example, the following SPARQL query shows the different units associated with the quantity kind quantitykind:Force:
SELECT ?qk ?qku ?qkl
WHERE {
BIND (quantitykind:Force AS ?arg1) .
?qk rdf:type qudt:QuantityKind .
FILTER (?qk = ?arg1) .
?qku qudt:hasQuantityKind ?qk .
?qku a qudt:Unit .
?qku rdfs:label ?qkl .
} ORDER BY ?qku
which results in 16 values for ?qku:
qk qku qkl
quantitykind:Force unit:DYN Dyne
quantitykind:Force unit:KIP_F Kip
quantitykind:Force unit:KiloGM_F Kilogram Force
quantitykind:Force unit:KiloN KiloN
quantitykind:Force unit:KiloP Kilopond
quantitykind:Force unit:KiloPOND KiloPOND
quantitykind:Force unit:LB_F Pound Force
quantitykind:Force unit:MegaLB_F Mega Pound Force
quantitykind:Force unit:MegaN MegaN
quantitykind:Force unit:MicroN MicroN
quantitykind:Force unit:MilliN MilliN
quantitykind:Force unit:N Newton
quantitykind:Force unit:OZ_F Imperial Ounce Force
quantitykind:Force unit:PDL Poundal
quantitykind:Force unit:PlanckForce Planck Force
quantitykind:Force unit:TON_F_US TON_F_US
Here is where the power of the QUDT ontology starts to reveal itself. In the SI system of units, all physical measurements can be described in terms of 7 basic dimensions, and the associated base units:
- Amount of substance - mole (mole)
- Electric current - ampere (A)
- Length - meter (m)
- Luminous intensity - candela (cd)
- Mass - kilogram (kg)
- Temperature - kelvin (K)
- Time - second (s)
(Note that the choice of what the basic dimensions are could have been different. The SI community could have chosen Electric charge instead of Electric current, for example, in which case the Coulomb would have been the base unit for SI. This is important, because there are other systems of units, such as the CGS-EMU system, and the CGS-ESU system, that made different choices for the base dimensions.)
In QUDT every dimension vector is comprised of each of the above base dimensions and an associated exponent in the following way:
(Dimension1 * dimensional_exponent1) * (Dimension2 * dimensional_exponent2) * ...
This is repeated for all 7 dimensions and the dimensionless indicator in the following order:
Amount of substance, Electric current, Length, Luminous intensity, Mass, Temperature, Time, Dimensionless
The dimensions and the dimensionless value are indicated with single letter codes which, for the above dimensions and dimensionless are, in order, as above:
A E L I M H T D
An example for the QuantityKindDimensionVector associated with Force is:
qkdv:A0E0L1I0M1H0T-2D0
where the only non-zero exponents are for L (length), M (mass), and T (time), i.e., M1L1T-2. (Please note that in QUDT we add a coefficient for dimensionless quantity kinds. This is the last item, D, in the example above. When a quantity kind is dimensionless all the base units will have zero exponents except D. An example of a dimensionless quantity kind is TemperatureRatio:
qkdv:A0E0L0I0M0H0T0D1
Using the base dimensions is how you can determine whether one unit can be converted into another. They must be commensurate, which means they must be associated with the same "dimension vector". The dimension vector (known in QUDT as the QuantityKindDimensionVector_SI for the SI dimension vector) is simply a description of a given unit in terms of the appropriate powers of the underlying base dimensions. For example, speed is (Length / Time); acceleration is (Length / Time**2).
The QUDT vocabulary contains over a thousand units compliant with ISO 80000 and several other standards including IEC 61360. For example, we could execute the following SPARQL query to produce all of the units in the vocabulary associated with the base units of M * L / T^2. We get to this through the DimensionVector:
SELECT ?un ?unl
WHERE {
BIND ("A0E0L1I0M1H0T-2D0" AS ?arg1) .
?dv rdf:type qudt:QuantityKindDimensionVector_SI .
BIND (afn:localname(?dv) AS ?dvn) .
FILTER (fn:contains(fn:upper-case(?dvn), fn:upper-case(?arg1))) .
?qk qudt:hasDimensionVector ?dv .
?un qudt:hasQuantityKind ?qk .
?un rdfs:label ?unl .
} ORDER BY ?un
which produces the following:
un unl
unit:DYN Dyne
unit:KIP_F Kip
unit:KiloEV-PER-MicroM Kilo Electron Volt per Micrometer
unit:KiloGM_F Kilogram Force
unit:KiloN KiloN
unit:KiloP Kilopond
unit:KiloPOND KiloPOND
unit:LB_F Pound Force
unit:MegaEV-PER-CentiM Mega Electron Volt per Centimeter
unit:MegaLB_F Mega Pound Force
unit:MegaN MegaN
unit:MicroN MicroN
unit:MilliN MilliN
unit:N Newton
unit:OZ_F Imperial Ounce Force
unit:PDL Poundal
unit:PlanckForce Planck Force
unit:TON_F_US TON_F_US
Every unit has an associated quantity kind and dimension vector. You cannot add a speed to a temperature because Length / Time is different from Temperature. You can add a furlong to a kilometer, because they both have a dimension vector of Length. Of course, you need to convert one unit into the other before adding the numbers, which leads us to...
Each instance of Unit has a property called qudt:conversionMultiplier. The value of the multiplier tells you what number to multiply to convert a given unit into the SI version of that unit. So, for example the conversionMultiplier for an inch (unit:IN) is 0.0245. That is, 1 Inch equals 0.0245 Meters.
Measurements that have the same QuantityKind can often be combined mathematically. You can add two lengths, once you accommodate their conversion multipliers, but it doesn't make sense to add a length and a temperature - they are of different quantity kinds. As an example of how to use conversion multipliers in QUDT, consider the following relationship to calculate the circumference of a rectangle:
rectangleCircumference = 2 x length + 2 * width
Lets say that, for the purposes of discussion, the length is measured in inches (IN) and the width is measured in centimeters (CentiM). Then if the length is 19 and the width is 12 we could use the following to calculate the circumference in the base unit of Meters. The essence of the query, after doing some bindings for the values and the unit types, comes down to getting the conversion multipliers for the units and performing the calculation:
SELECT ?rectCircum
WHERE {
BIND (19 AS ?length) .
BIND (12 AS ?width) .
BIND (unit:IN AS ?arg1) .
BIND (unit:CentiM AS ?arg2) .
?arg1 qudt:conversionMultiplier ?cm1 .
?arg2 qudt:conversionMultiplier ?cm2 .
BIND (((2 * ?length * ?cm1) + (2 * ?width * ?cm2)) AS ?rectCircum) .
}
The query above produces the value of 1.2052, which is now in SI units of meter (M). Of course, we could add another last line (e.g., BIND ((?rectCircum / ?cm1) AS ?rectCircumIN) ., which produces 47.44881 in, or BIND ((?rectCircum / ?cm2) AS ?rectCircumCentiM) ., which produces 120.52 cm) to the query to return the circumference in either inches or centimeters, respectively. Alternatively, we could have just converted one of the two (length or width) to the other before calculating the circumference.
Building on the above discussion of dimension vectors and conversion multipliers leads us to an elegant way to do unit conversions. (Important caveat: The following example works to convert incremental values of units where the only important factor is the relative size of the unit. This example does not handle absolute values for units with offsets (think Celsius and Fahrenheit degrees). QUDT supports that too - the QUDT treatment of absolute and incremental values is discussed here.
The approach we will use is shown in the following pseudocode:
1. start with a given instance of a Unit
1.1 find out what QuantityKind it has
1.1.1 determine its QuantityKindDimensionVector
1.2 find out all the QuantityKinds that have that same QuantityKindDimensionVector
1.3 find all the Units with those QuantityKinds
2. multiply your starting unit by its conversionMultiplier
2.1 divide the result by the target unit conversionMultiplier
That is the logic behind the following SPARQL query:
PREFIX rdfs: <http://www.w3.org/2000/01/rdf-schema#>
PREFIX qudt: <http://qudt.org/schema/qudt/>
SELECT DISTINCT ?toConvert ?label ?into ?otherUnitLabel ?multiplyBy ?multiplier
WHERE {
BIND ("To convert" AS ?toConvert) .
BIND ("into" AS ?into) .
BIND ("multiply by" AS ?multiplyBy) .
?unit a qudt:Unit .
?unit rdfs:label ?label .
FILTER(CONTAINS (LCASE(STR(?label)), "milligray")) .
?unit qudt:conversionMultiplier ?cm1 .
?unit qudt:hasQuantityKind/qudt:hasDimensionVector ?qkdv .
?otherUnit qudt:hasQuantityKind/qudt:hasDimensionVector ?qkdv .
?otherUnit a qudt:Unit .
FILTER (?otherUnit != ?unit) .
?otherUnit qudt:conversionMultiplier ?cm2 .
?otherUnit rdfs:label ?otherUnitLabel .
BIND ((?cm1/?cm2) AS ?multiplier) .
}
ORDER BY ?label ?multiplier
Executing this query produces output that looks like this:
To convert MilliGRAY into Kilocalorie per Gram multiply by 2.390057361376673E-10
To convert MilliGRAY into MegaJ PER KiloGM multiply by 1.0E-9
To convert MilliGRAY into CAL_IT PER GM multiply by 2.388458966274959E-7
To convert MilliGRAY into calorieIT per gram (calIT/g) multiply by 2.388458966274959E-7
To convert MilliGRAY into CAL_TH PER GM multiply by 2.390057361376673E-7
To convert MilliGRAY into calorieTH per gram (calTH/g) multiply by 2.390057361376673E-7
To convert MilliGRAY into BTU-IT-PER-lb multiply by 4.299226139294927E-7
To convert MilliGRAY into British Thermal Unit (TH) Per Pound multiply by 4.30210433032265E-7
To convert MilliGRAY into J PER GM multiply by 1.0E-6
To convert MilliGRAY into BTU_IT PER LB_F multiply by 4.216100966554345E-6
To convert MilliGRAY into Gray multiply by 0.001e0
To convert MilliGRAY into Joule per Kilogram multiply by 0.001e0
To convert MilliGRAY into Sievert multiply by 0.001e0
To convert MilliGRAY into Rad multiply by 0.1e0
To convert MilliGRAY into Rem multiply by 0.1e0
To convert MilliGRAY into MilliSV multiply by 1.0e0
To convert MilliGRAY into ERG PER GM multiply by 10.0e0
To convert MilliGRAY into Erg per Gram multiply by 10.0e0
To convert MilliGRAY into MilliR equivalent man multiply by 3875.968992248062e0
To convert MilliGRAY into MilliR multiply by 3875.968992248062e0
None of these pairwise relationships had to be stored. The query simply returns all the other units that have the same associated dimension vector. You can try queries for both incremental and absolute unit conversion using our EDG server. There is an introductory video there that shows how to bring up the SPARQL query interface.
A whole category of units are actually dimensionless, and QUDT has a specific modeling pattern to handle these. Think about the unit "relative humidity" which is generally expressed as a percentage. In QUDT, the instance is unit:PERCENT_RH. While the unit is a dimensionless number, it is actually the ratio of two partial pressures, and the dimensions cancel out because of the ratio. It is important to capture this, because it would be nonsensical to compare a relative humidity percentage with a savings account yield percentage, even though they are both just nondimensional percentages.
To capture the full semantics, unit:PERCENT_RH points to quantitykind:PressureRatio using the qudt:hasQuantityKind relation. The quantitykind:PressureRatio has a dimensionality that is the result of a combination of other quantity kinds. In this specific case, it is the ratio of two pressures. quantitykind:PressureRatio points to the dimension vector of qkdv:A0E0L0I0M0H0T0D1 (the dimensionless dimension vector), but it also has two other properties, qudt:qkdvDenominator and qudt:qkdvNumerator. In this example, they are both populated with qkdv:A0E0L-1I0M1H0T-2D0, the dimension vector for a pressure. Using this pattern, the model captures the fact that unit:PERCENT_RH is dimensionless, but also that it derives from the ratio of two pressures.
Finally, quantitykind:PressureRatio also uses the skos:broader relation to position it in a hierarchy that, in this case, broadens to quantitykind:DimensionlessRatio, and then to quantitykind:Dimensionless.
Here's a diagram that shows the final result:

Most of the dimensionless quantity kind instances are simple ratios of a single kind of quantitykind, but this may not always be the case. Sometimes the final dimensionality hides the fact that some of the dimensions in the definition formula "cancel out", and this can be made explicit using the numerator and denominator properties.
On rare occasions, one encounters a quantity kind that has no dimension vector. (Normally, all quantity kinds are required to have an associated dimension vector). It is important to recognize this as distinct from quantity kinds that have a dimensionless dimension vector (i.e. A0E0L0I0M0H0T0D1). These quantity kinds might be useful to refer to in some specialized domain, but they are ambiguous. For example, quantitykind:VisionThresholds refers to the sensitivity of the eye to light. It might be reported as the number of photons incident on a prescribed part of the retina, or it might be in terms of luminance, or even illuminance. It is arguable that such concepts don't really even belong in QUDT as defined Quantity Kinds and are best treated as contextual Quantity instances instead. As of the writing of this wiki, QUDT only has 7 such quantity kinds.
Let's say your smart thermostat is even smarter than the one in the first example, and communicates in both Fahrenheit and Kelvin (the SI unit for temperature). Here's how we could store all that information. Keep in mind that the "concept" of the temperature setting is still a single concept, even when its value is represented in multiple units. So in this case, instead of using the built-in data property qudt:hasUnit inside the qudt:Quantity class, we use the object property qudt:quantityValue that points to the class qudt:QuantityValue in the first diagram on this page. There will be two instances of qudt:QuantityValue, one that points to the unit:DEG_F unit instance, and one that points to the unit:K unit instance. Here's the code:
wiki-examples:MySmarterThermostatSetting
a qudt:Quantity ;
qudt:quantityValue wiki-examples:FahrenheitSetting ;
qudt:quantityValue wiki-examples:KelvinSetting ;
.
wiki-examples:FahrenheitSetting
rdf:type qudt:QuantityValue ;
qudt:hasUnit unit:DEG_F ;
qudt:value "72.0"^^xsd:float ;
.
wiki-examples:KelvinSetting
rdf:type qudt:QuantityValue ;
qudt:hasUnit unit:K ;
qudt:value "295.37"^^xsd:float ;
.