This repository contains two segments. The first deals with the implementation of gradient descent for polynomial regression in two variables. The second segment explores the use of Bayesian methods for parameter estimation.
This section is focused on the implementation of the gradient descent algorithm for the purpose of optimally fitting a curve to the data. Techniques for regression explored are batch and stochastic gradient descent, as well as the normal equation method to obtain an analytical solution. Various degrees of polynomials may be fit to the data, and their performance analyzed. To analyze how well a model fits the data, we use the Root Mean Squared Error (RMSE) and the R2 score as metrics of performance.
The dataset used for developing our regression model may be found at https://archive.ics.uci.edu/ml/datasets/3D+Road+Network+%28North+Jutland%2C+Denmark%29
This dataset was constructed by adding elevation information to a 2D road network in North Jutland, Denmark.
The attributes of the data are as follows :
- OSM_ID : OpenStreetMap ID for each road segment or edge in the graph.
- LONGITUDE : Web Mercaptor (Google format) longitude
- LATITUDE : Web Mercaptor (Google format) latitude
- ALTITUDE : Height in meters.
The dataset contains 434874 instances.
For the purpose of our regression model, we use the attributes LONGITUDE and LATITUDE to predict ALTITUDE.
This next section explores the use of Bayesian methods to estimate population parameters which would describe a probability distribution most suited to have given rise to the data observed.
In the Bayesian approach, we do not content ourselves with a single valued estimate for the parameters of the underlying distribution (as we would have done in a maximum likelihood estimate), but instead look to estimate a distribution representing how likely different values of these parameters would be. This, in turn, introduces the notion of prior and posterior probability distributions for the parameter to be estimated, as per Bayes' Theorem.
In particular, we concern ourselves with the standard biased coin toss problem. We are interested in estimating a distribution that would model the probability of landing a head when the coin is tossed.
We know that the coin toss problem can be modeled as data generated from a binomial distribution. The probability of landing a head p, given only n observations is what we are interested in estimating.
We use the fact that the conjugate prior of a Binomial distribution is a beta distribution to estimate p, by applying Bayes' theorem to obtain the posterior distribution for p, given only our set of observed data points.
There are two methods of approach:
-
Sequential Approach : Here, we look at each data point sequentially and update the estimate of the posterior distribution repetitively by taking the previous estimate as the prior for the next estimate.
-
By Looking at the Entire Dataset at Once : Here, we calculate the posterior distribution, having seen the entire dataset at once, using our initially assumed prior distribution.
For each of these methods, we implement both the numerical and analytical variants of estimation.
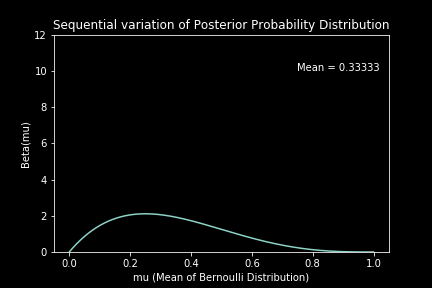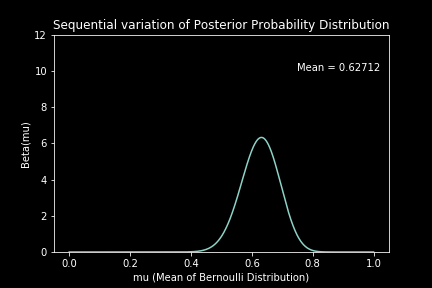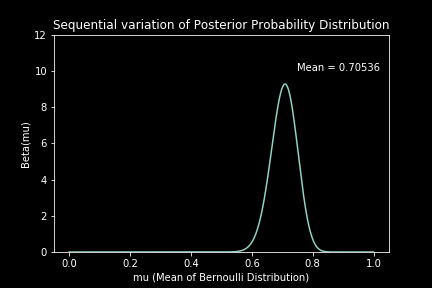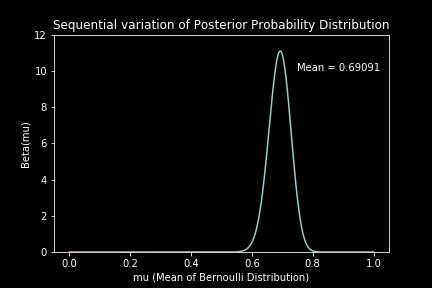
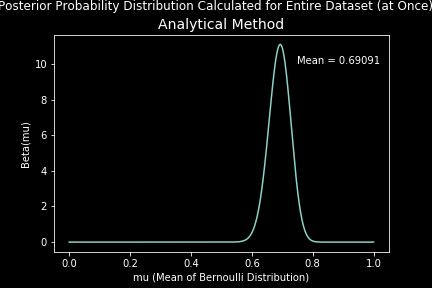
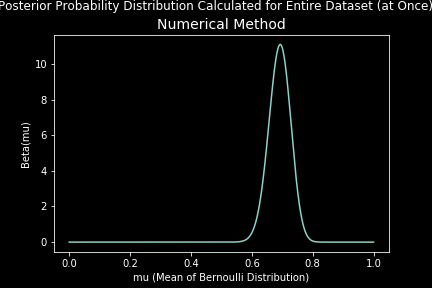
For the case of 160 observations (n = 160) with (p = 0.7), our estimation converges to a beta distribution with mean 0.69091. The estimation using the sequential method can be seen visually as below:
Both the sequential method and observing-dataset-at-once method yielded the same results. The numerical and analytical approaches to computation also made no difference, as was anticipated.