Skip to content

Model Programs

Jump to bottom
Romesh Abeysuriya edited this page Mar 20, 2018 · 1 revision

New programs system

As discussed in the integration overview, the transition rates supplied by the Link objects are governed by the values stored in Parameter objects. The role of the Programs module is to provide a function that computes parameter values as a function of spending. Thus, the inputs to the Programs module are spending amounts, and the outputs are parameter values that can be used to overwrite the original values during integration.

Programs

A program is the basic unit in the programs system - a single intervention that money can be spent on. It consists of

  • A set of parameters in the cascade that the program will provide values for
  • A set of attributes that are effectively dependent parameters internal to the program, that are used to compute the cascade parameter values
  • For each target parameter, a function that maps the attributes onto the parameter value

For example, consider the program below

Name: DS Targeted Diagnosis Program

Attribute ID Attribute Name
sens Sensitivity (Detection Probability)
lat_ident Latents Identified (Per DS-TB Case)
effic Latent Treatment Efficacy (After Completed Treatment)
adher Latent Treatment Adherence Probability (Yearly)
dur Latent Treatment Duration (Months)
Impact parameter Function Impact group
lteyes_rate lat_ident a
lteno_rate lat_ident*(1-adher) b
ltesuc_rate lat_ident*(1-(1-effic)^(12.0/dur)) c
spddiag_rate sens d
snddiag_rate sens d

This program has 5 attributes, and a set of 5 impact parameters (target parameters) some of which directly correspond to attributes, and some of which are derived from the attributes. Each attribute gets a time-varying entry in the databook for the user to supply values. The impact parameters can only depend on attributes of the program (i.e., they cannot refer to attributes in other programs, cascade parameters, or characteristics).

All programs have a unit cost which is used to calculate coverage on the assumption that the number of people covered is given by dividing spending on the program by the unit cost. In this case, the program's coverage will be a number of people. Alternatively, the unit cost can be interpreted as the cost required to increase the fraction of the population covered by 1 percent. Then the program's coverage will be a fraction.

A program is defined as reaching parameters in a set of populations - the populations reached are specified in the databook. Coverage of a program is assumed to be aggregated. That is, the number of people covered are uniformly distributed across the populations that it reaches, in proportion to their relative sizes. So for example, if a program is allocated $500 and the unit cost is $2, then 250 people will be covered. Suppose it reaches populations A and B. Then the program will reach A/(A+B) people in population A, and B/(A+B) people in population B. So if there were 2000 people in population A and 500 people in population B, then the program would reach 200 people in population and 50 people in population B.

Recall that a population contains a copy of the entire cascade, so when we say that 200 people were reached in population A, this number is global to the entire cascade in that population. In cases where programs have multiple effects that are not mutually exclusive, the entire coverage can be applied to every parameter. For example, if a program affects both treatment uptake and treatment success, it may make sense to use the entire coverage of 200 people to compute the impact for each parameter. On the other hand, if the transitions are mutually exclusive (e.g. a person can be smear-positive (SP) and have treatment uptake, or smear-negative (SN) and have treatment uptake, but they cannot be both SP and SN) then the coverage may need to be distributed across the transitions. This is done by disaggregating parameters across their source compartments. In the case of SP and SN, the relevant compartments might be diagnosed SP (SPD) and diagnosed SN (SND). Of the 2000 people in population A, suppose 400 were SPD and 100 were SND. Then, the 200 people covered by the program would be further disaggregated into 160 SPD and 40 SND. To implement this, the parameters can optionally be assigned impact groups. Coverage is assumed to correspond to people reached by all of the parameters with an impact group, and is thus disaggregated over the entire group. For the table above, the first three parameters each use the entire coverage of the program (within a given population) while the last two parameters split their coverage across their source compartments.

Note that while a program can target any parameter, disaggregation is only performed when targeting a transition parameter. That is, any non-transition parameters which are targeted (such as the number of people on ART, num_art) are implicitly considered to be in their own impact group.

Lastly, the program specification in the cascade workbook defines a type of program, akin to a template. The actual programs present are specified in the databook. Thus, program specification is a two step process:

  • The cascade defines a program template in terms of attributes and parameters reached. Example might be 'Strain diagnosis program'
  • The databook defines actual programs as instances of program templates, reaching particular populations and with independently set parameter values and unit costs. Examples might be 'Enhanced Mass Screening at PHC facilities' and 'Mass Screening/Outreach in High Risk Areas' (both of which are instances of strain diagnosis programs)

The program label refers to the databook label e.g. 'Enhanced Mass Screening at PHC facilities' has ENH-MS-PHC, while the program type refers to the cascade code label e.g. 'Strain Diag Program' is pt_str_diag.

Workflow

Now that we have an overview of what a program is, we can go through the process of computing a set of parameter values. The cascade defines a particular type of program, as defined above. The databook specifies potentially several instances of these programs, reaching different populations and with different attribute values. Thus, it is usually the case that multiple programs all contribute to the same parameter value. The workflow for computing programs therefore necessarily takes place at the level of a set of programs. An overview of the programs workflow is shown below

It is highly recommended to download a high-resolution PDF of this image for reference. This document will now go over each of the stages shown in detail, by walking through an example of how to compute a parameter value when multiple programs are present.

Model Structure

Consider a toy model as shown above. In each population, there are two parameters. Each parameter supplies values for two links. Each link has a source compartmennt. The number of people reached by a parameter is computed by summing all of the associated source compartments - so 'Parameter 1 Pop 1' reaches a number of people given by summing 'Source Compartment 1' and 'Source Compartment 2'

Program Specification

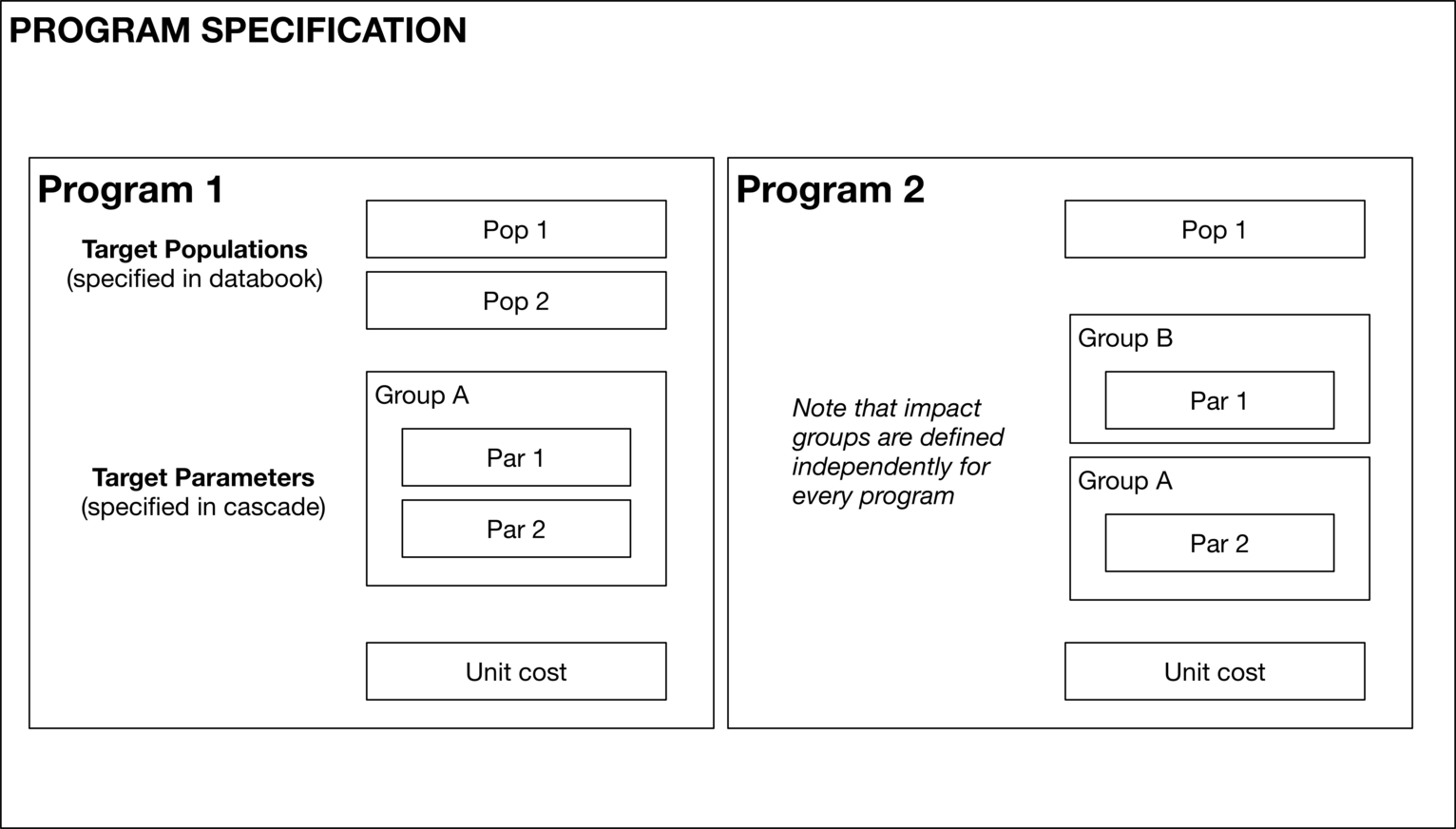
For this example, we will consider two programs, that each reach Parameters 1 and 2. Program 1 will reach both populations, while Program 2 only reaches Pop 1. The first program has both the parameters in the same impact group, while the second program has the parameters in different impact groups. Note that the impact groups can be defined independently for each program.

Stage 1 - Net coverage/impact

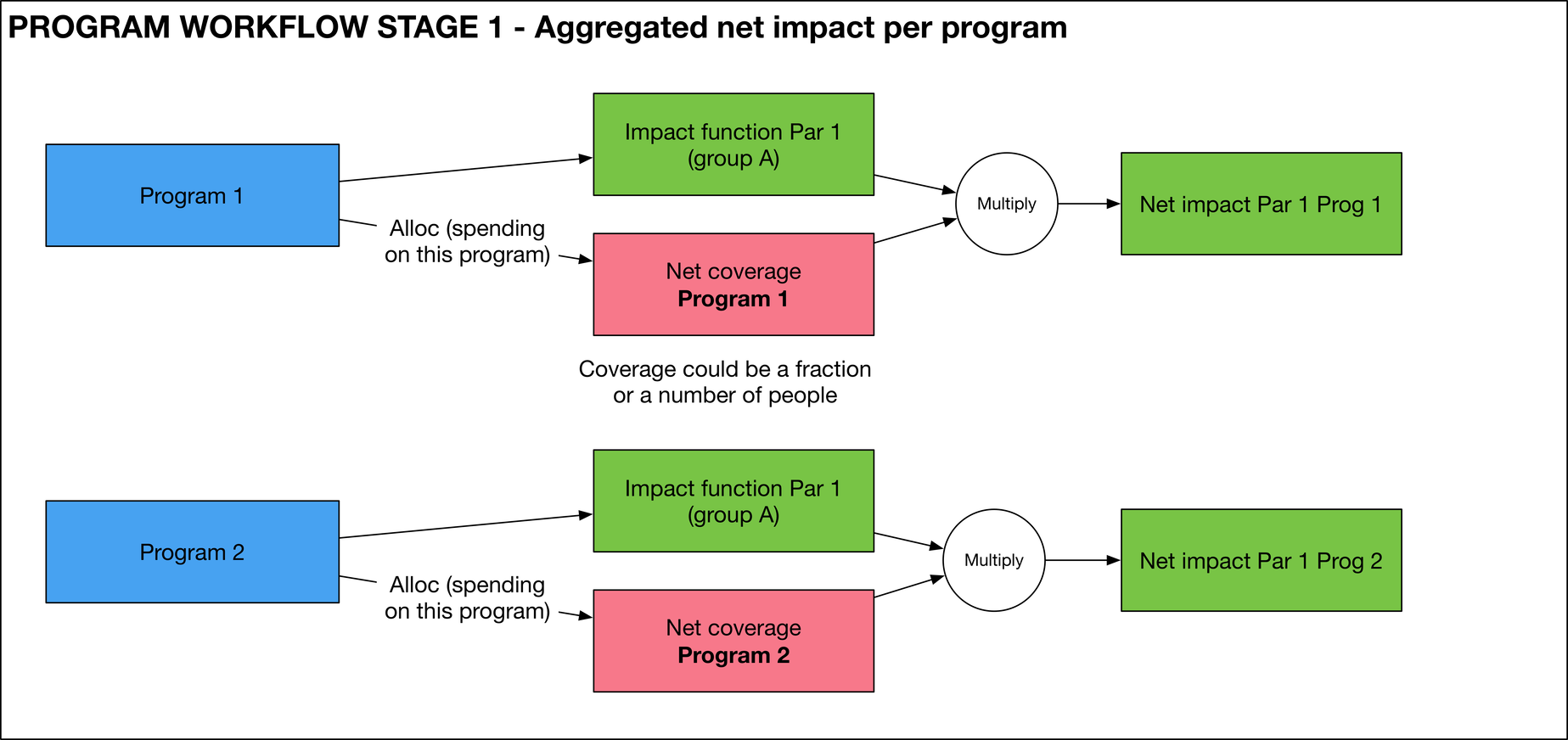
In the first stage, the net coverage and net impact are evaluated for every program. Each program has a single net coverage value, obtained by dividing the budget by the unit cost. A program has a net impact value for every parameter it reaches. First, for each parameter, the impact function is evaluated. Then, the impact function is multiplied by the net coverage to yield the net impact for that parameter.

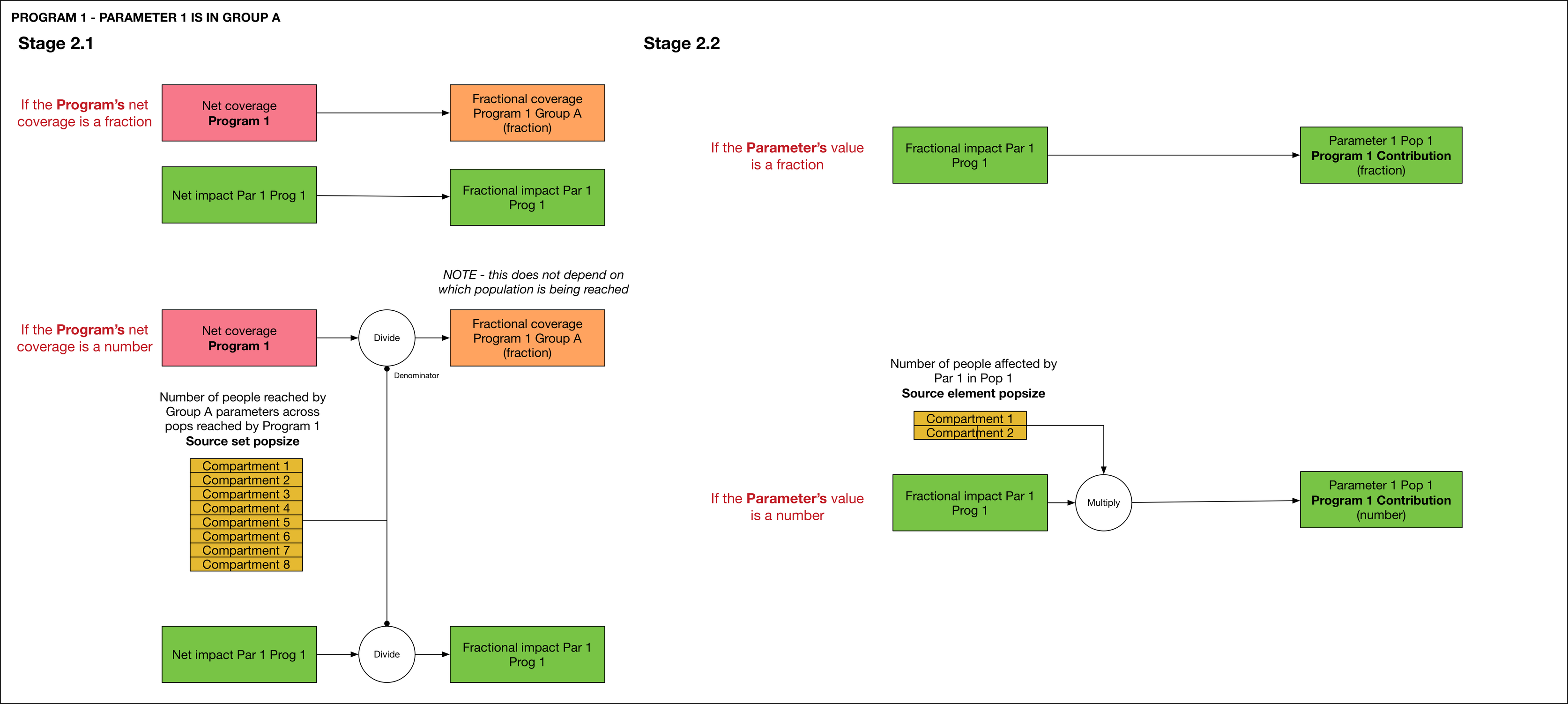
Stage 2 - Fractional coverage, Parameter contribution

In the second stage, conversion from fraction to number units is performed. This occurs in two stages - first, depending on the program's units, and then, depending on the parameter's units.

The fractional coverage refers to the fraction of people in each impact group that are being reached by this program. For example, if the impact group reaches 1000 people, and the program's net coverage is 200, then the fractional coverage is 0.2. If the program has coverage that is in units of fraction, then no conversion is necessary based on the program's units. If the program has number units, then the net coverage is divided by the number of people reached by the impact group. The number of people is obtained by summing the source compartments for all programs that belong to the impact group, across all populations. As shown in the figure above, Program 1 reaches Parameters 1 and 2 in both populations 1 and 2. Therefore, Compartments 1-8 are all included in this sum. The impact is also rescaled in the same way, to yield the fractional impact. Note that the fractional coverage is specified for each impact group, but the fractional impact is specified for each parameter. The fractional coverage for a particular parameter is simply given by looking up the fractional coverage of the impact group it belongs to.

After the first rescaling, the fractional coverage and fractional impact are both in units of 'fraction'. A second rescaling step is required if the parameter is in number units. If the parameter has number units, then the fractional impact is multiplied by the number of people reached by the parameter in question. This is specific to the Parameter object, and thus refers to a single parameter in a single population. In the example shown above, for Parameter 1 in Pop 1, the relevant population size is obtained by summing Compartments 1 and 2 only. This yields the program's 'contribution' for the parameter. If the parameter's units are 'fraction', then the fractional impact can be directly used as the contribution. The calculation for the other parameters, and for Program 2, proceeds in the same way - an example is shown in the full image.

The end result of this stage is that within a program, each parameter has a fractional coverage and parameter contribution value for every parameter it reaches.

Stage 3 - Scaling fractional coverage

In the third stage, cases where multiple programs contribute to the same parameter are resolved. First, for each Parameter object, all of the contributions made by all of the programs are identified. In this case, Program 1 and Program 2 both contribute to Parameter 1 in population 1. Next, the fractional coverages are added together. If the sum of the fractional coverages are less than 1, then no rescaling is necessary, and the parameter value contributions are unchanged. However, if the sum of the fractional coverages is greater than 1, then the parameter values are rescaled by this sum. So for instance, if the sum of fractional coverages was 1.5, then each parameter contribution is divided by 1.5.

The implication of this is that coverages do not overlap within a compartment, and thus programs compete to control the transition parameter value. It is worth noting that for a single program, the value of the impact parameter computed based on the cascade formula and databook values corresponds exactly to the transition parameter value when there is complete coverage. To have complete coverage, the program must either

  • Have units of fraction, and a coverage value of 1.0
  • Have a numerical coverage value equal to the number of people reached by the parameter (and have the parameter belong to its own impact group)
  • Not have any other programs reaching the same parameter (or else the coverages will be rescaled)

Stage 4 - Value aggregation

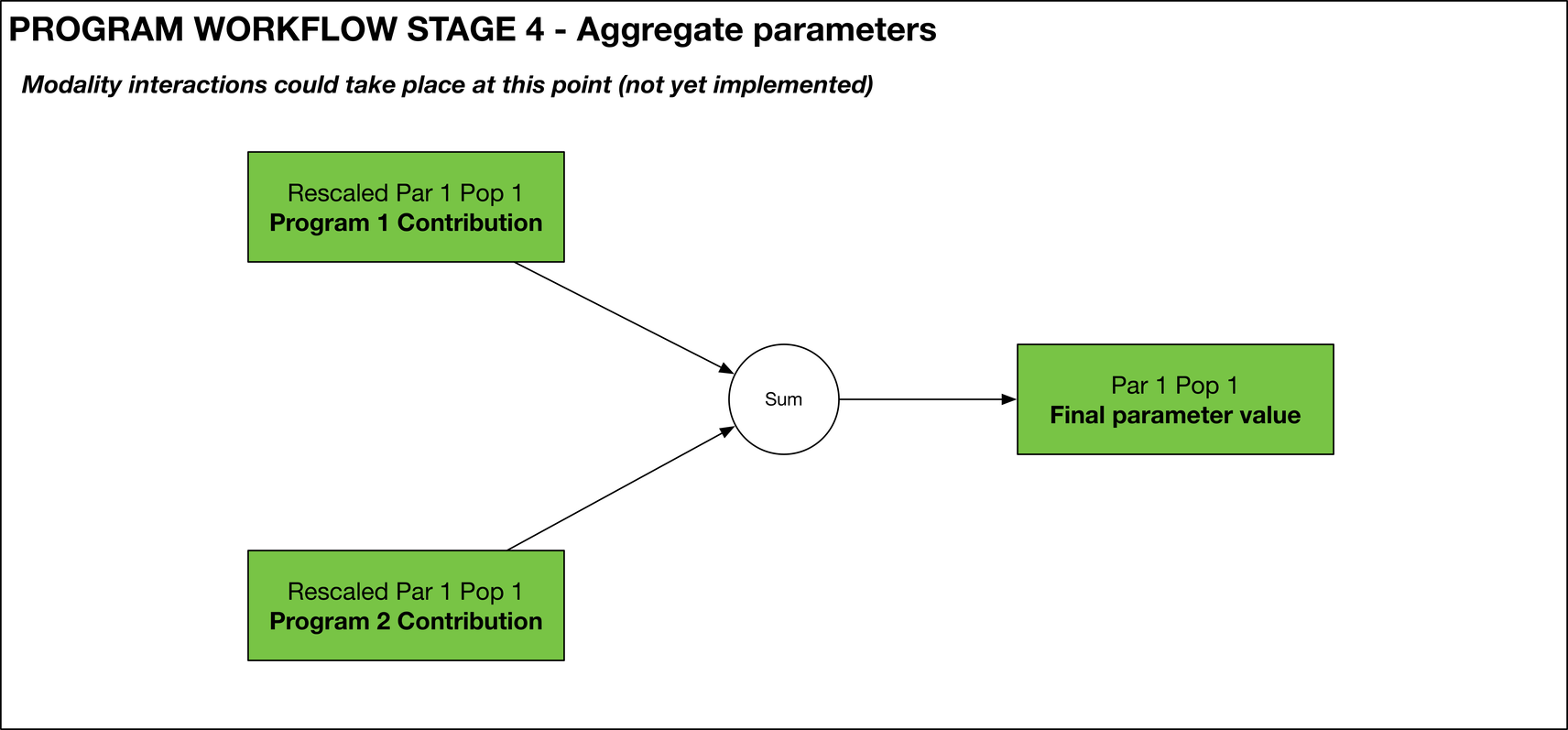
Finally, all of the (rescaled) contributions are aggregated to provide a single parameter value - currently, this is performed simply by adding all of the contributions together.

Implementation

There are four classes relevant for programs - Program and ProgramSet, which are the original object, and ModelProgram and ModelProgramSet which are wrappers used to facilitate integration.

Program and ProgramSet

A Program is the fundamental unit for the Programs system in OptimaTB. It contains

self.t = Time index for data
self.cost = Spending data
self.cov = Coverage data
self.cost_format = cost_format
self.cov_format = whether coverage is a fraction or a number
self.attributes = attributes local to the program
self.target_pops = labels for target populations
self.target_pars = labels for target parameters
self.func_specs = functions for computing impact

The Program also supplies key methods

  • getCoverage - return coverage as a function of spending
  • getImpact - return impact as a function of coverage
  • getBudget - return budget as a function of coverage (i.e. inverse of the cost-coverage function)
  • interpolate - program attributes are time-varying but may contain missing data, this function fills missing values
  • getDefaultBudget - returns the interpolated spending on the program based on stored data

Recall that the impact parameter is the impact function multiplied by the coverage. This calculation is implemented in getImpact.

Typically, Program object are instantiated from within a ProgramSet. The ProgramSet is quite lightweight, its main role is to construct an array of programs given data and settings. This in turn is generated by project.makeProgset.

ModelProgram and ModelProgramSet

These objects map directly onto the computation stages shown here, and have corresponding methods to do these calculations. A ModelProgramSet contains a ProgramSet which is supplied at construction. For each Program in the ProgramSet, the ModelProgramSet instantiates a ModelProgram object.

A ModelProgram has the following key attributes:

  • pars is a list of Parameter objects that this ModelProgram supplies values for
  • impact_groups is a dict where the key is the group label, and the value is a list of Parameter objects belonging to that group
  • is_fraction specifies the program's coverage units (used for the first part of the Stage 2 calculation)
  • is_active is a flag that can enable or disable programs. This is set to False if a program was disabled e.g. by not having any funding specified for it
  • net_dt_cov stores precomputed values for net coverage
  • net_dt_impact stores precomputed values for net impact
  • get_contribution(ti) returns an dict where the key is a parameter UUID and the value is a (fractional coverage, contribution) tuple. This corresponds to the output of Stage 2 in the calculation above

A ModelProgramSet has the following key attributes:

  • programs is a list of ModelProgram objects
  • progset is a ProgramSet object
  • pars is a set of Parameter objects
  • dt is the timestep size, used to convert between annualized and timestep based units
  • update_cache(alloc,tvals,dt) is analogous to the old preCalculateProgsetVals. Noting that the Stage 1 computation can be carried out independently of any compartment sizes, update_cache() will precalculate the net coverage and net impact, and store them in the ModelProgramSet attributes net_dt_cov and net_dt_impact. Note that this function takes in an alloc which is a dict where the key is a program label, and the value is the spending amount for that program for each year in the simulation.
  • get_alloc(sim_settings) takes in the sim settings, and returns an allocation for use in update_cache(). The computation of spending is nontrivial. First, the sim settings can define an initial_alloc as a single spending value for each program in use. By default, this spending value is used at all times between the program start and end year. If there are ramp constraints, then it takes a period of time for the funding to change from the default spending (the values contained within the Program object) to the specified allocation. If a program does not appear in the initial allocation, then it will be disabled and not included in the parameter overwrites unless the saturate_with_default_budgets is enabled. If this flag is True, then programs without a specified allocation will automatically recieve the amount of funding specified in its default budget.
  • compute_pars(ti) is called after using update_cache. It first calls get_contribution() for each ModelProgram object. Then, it implements Stages 3 and 4 of the program calculation. The output of this function is a dict where the key is a parameter UUID and the value is the parameter's program-calculated value at time index ti

Thus, to summarize the implementation of the programs workflow

  • Stage 1 is implemented in ModelProgramSet.update_cache()
  • Stage 2 is implemented in ModelProgram.get_contribution()
  • Stages 3 and 4 are implemented in ModelProgramSet.compute_pars()

The structure of these methods is desiged to facilitate reconciliation as well - the reconciliation script updates the program attributes, then calls ModelProgramSet.update_cache() and ModelProgramSet.compute_pars(), and finally compares the returned parameter values with the target parset values.

Future development

Program interactions could be implemented as different calculations in Stage 3 and Stage 4 of the workflow

Clone this wiki locally