LassoNet

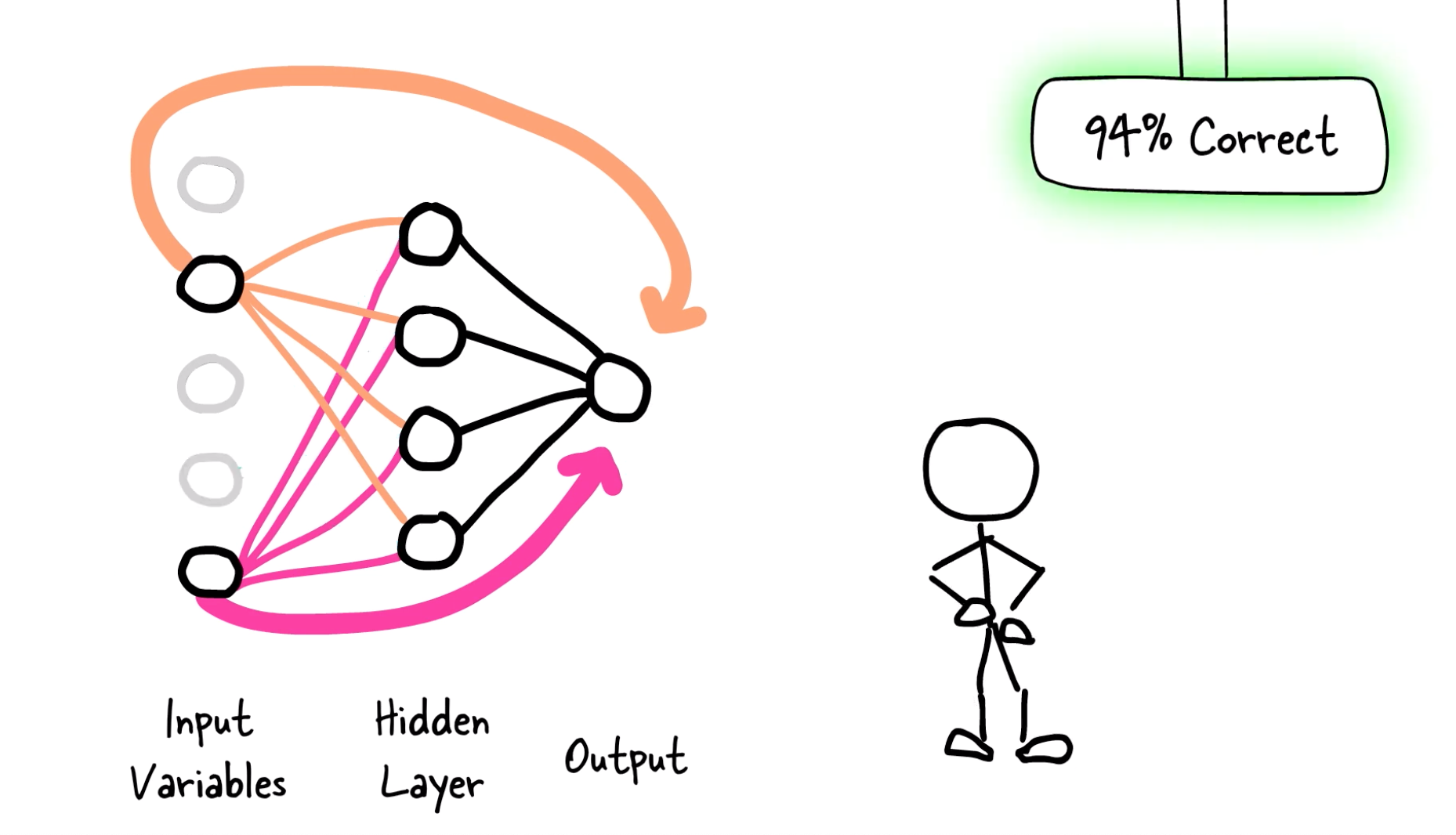
LassoNet is a new family of models to incorporate feature selection and neural networks.

LassoNet works by adding a linear skip connection from the input features to the output. A L1 penalty (LASSO-inspired) is added to that skip connection along with a constraint on the network so that whenever a feature is ignored by the skip connection, it is ignored by the whole network.

Installation

pip install lassonet

Usage

We have designed the code to follow scikit-learn's standards to the extent possible (e.g. linear_model.Lasso).

from lassonet import LassoNetClassifierCV 
model = LassoNetClassifierCV() # LassoNetRegressorCV
path = model.fit(X_train, y_train)
print("Best model scored", model.score(X_test, y_test))
print("Lambda =", model.best_lambda_)

You should always try to give normalized data to LassoNet as it uses neural networks under the hood.

You can read the full documentation or read the examples that cover most features. We also provide a Quickstart section below.

Quickstart

Here we guide you through the features of LassoNet and how you typically use them.

Task

LassoNet is based on neural networks and can be used for any kind of data. Currently, we have implemented losses for the following tasks:

• regression: LassoNetRegressor
• classification: LassoNetClassifier
• Cox regression: LassoNetCoxRegressor
• interval-censored Cox regression: LassoNetIntervalRegressor

If features naturally belong to groups, you can use the groups parameter to specify them. This will allow the model to put a penalty on groups of features instead of each feature individually.

Data preparation

You should always normalize your data before passing it to the model to avoid too large (or too small) values in the data.

What do you want to do?

The LassoNet family of models do a lot of things.

Here are some examples of what you can do with LassoNet. Note that you can switch LassoNetRegressor with any of the other models to perform the same operations.

Using the base interface

The original paper describes how to train LassoNet along a regularization path. This requires the user to manually select a model from the path and made the .fit() method useless since the resulting model is always empty. This feature is still available with the .path(return_state_dicts=True) method for any base model and returns a list of checkpoints that can be loaded with .load().

from lassonet import LassoNetRegressor, plot_path

model = LassoNetRegressor()
path = model.path(X_train, y_train, return_state_dicts=True)
plot_path(model, X_test, y_test)

# choose `best_id` based on the plot
model.load(path[best_id].state_dict)
print(model.score(X_test, y_test))

You can also retrieve the mask of the selected features and train a dense model on the selected features.

selected = path[best_id].selected
model.fit(X_train[:, selected], y_train, dense_only=True)
print(model.score(X_test[:, selected], y_test))

You get a model.feature_importances_ attribute that is the value of the L1 regularization parameter at which each feature is removed. This can give you an idea of the most important features but is very unstable across different runs. You should use stability selection to select the most stable features.

Using the cross-validation interface

We integrated support for cross-validation (5-fold by default) in the estimators whose name ends with CV. For each fold, a path is trained. The best regularization value is then chosen to maximize the average score over all folds. The model is then retrained on the whole training dataset to reach that regularization.

model = LassoNetRegressorCV()
model.fit(X_train, y_train)
model.score(X_test, y_test)

You can also use the plot_cv method to get more information.

Some attributes give you more information about the best model, like best_lambda_, best_selected_ or best_cv_score_.

This information is useful to pass to a base model to train it from scratch with the best regularization parameter or the best subset of features.

Using the stability selection interface

Stability selection is a method to select the most stable features when running the model multiple times on different random subsamples of the data. It is probably the best way to select the most important features.

model = LassoNetRegressor()
oracle, order, wrong, paths, prob = model.stability_selection(X_train, y_train)

• oracle is a heuristic that can detect the most stable features when introducing noise.
• order sorts the features by their decreasing importance.
• wrong[k] is a measure of error when selecting the k+1 first features (read this paper for more details). You can plt.plot(wrong) to see the error as a function of the number of selected features.
• paths stores all the computed paths.
• prob is the probability that a feature is selected at each value of the regularization parameter.

In practice, you might want to train multiple dense models on different subsets of features to get a better understanding of the importance of each feature.

For example:

for i in range(10):
    selected = order[:i]
    model.fit(X_train[:, selected], y_train, dense_only=True)
    print(model.score(X_test[:, selected], y_test))

Important parameters

Here are the most important parameters you should be aware of:

• hidden_dims: the number of neurons in each hidden layer. The default value is (100,) but you might want to try smaller and deeper networks like (10, 10).
• path_multiplier: the number of lambda values to compute on the path. The lower it is, the more precise the model is but the more time it takes. The default value is a trade-off to get a fast training but you might want to try smaller values like 1.01 or 1.005 to get a better model.
• lambda_start: the starting value of the regularization parameter. The default value is "auto" and the model will try to select a good starting value according to an unpublised heuristic (read the code to know more). You can identify a bad lambda_start by plotting the path. If lambda_start is too small, the model will stay dense for a long time, which does not affect performance but takes longer. If lambda_start is too large, the number of features with decrease very fast and the path will not be accurate. In that case you might also want to decrease lambda_start.
• gamma: puts some L2 penalty on the network. The default is 0.0 which means no penalty but some small value can improve the performance, especially on small datasets.
• more standard MLP training parameters are accessible: dropout, batch_size, optim, n_iters, patience, tol, backtrack, val_size. In particular, batch_size can be useful to do stochastic gradient descent instead of full batch gradient descent and to avoid memory issues on large datasets.
• M: this parameter has almost no effect on the model.

Features

• regression, classification, Cox regression and interval-censored Cox regression with LassoNetRegressor, LassoNetClassifier, LassoNetCoxRegressor and LassoNetIntervalRegressor.
• cross-validation with LassoNetRegressorCV, LassoNetClassifierCV, LassoNetCoxRegressorCV and LassoNetIntervalRegressorCV
• stability selection with model.stability_selection()
• group feature selection with the groups argument
• lambda_start="auto" heuristic (default)

Note that cross-validation, group feature selection and automatic lambda_start selection have not been published in papers, you can read the code or post as issue to request more details.

We are currently working (among others) on adding support for convolution layers, auto-encoders and online logging of experiments.

Website

LassoNet's website is https:lasso-net.github.io/. It contains many useful references including the paper, live talks and additional documentation.

References

• Lemhadri, Ismael, Feng Ruan, Louis Abraham, and Robert Tibshirani. "LassoNet: A Neural Network with Feature Sparsity." Journal of Machine Learning Research 22, no. 127 (2021). pdf bibtex
• Yang, Xuelin, Louis Abraham, Sejin Kim, Petr Smirnov, Feng Ruan, Benjamin Haibe-Kains, and Robert Tibshirani. "FastCPH: Efficient Survival Analysis for Neural Networks." In NeurIPS 2022 Workshop on Learning from Time Series for Health. pdf
• Meixide, Carlos García, Marcos Matabuena, Louis Abraham, and Michael R. Kosorok. "Neural interval‐censored survival regression with feature selection." Statistical Analysis and Data Mining: The ASA Data Science Journal 17, no. 4 (2024): e11704. pdf