MCU board id implementation details

The mcu-0.6 and mcu144-0.6 modules contain a built-in "Board ID" detection mechanism which allows the firmware to distinguish between different Hellen boards.

The idea

The main idea is to measure the capacitor charge/discharge time through a series resistors using standard digital I/O pins. One pin is used to provide a Vcc(3.3) or Vdd(0) voltage to the capacitor through a resistor, and another pin is used as a digital input. Then vice versa.

The algo:

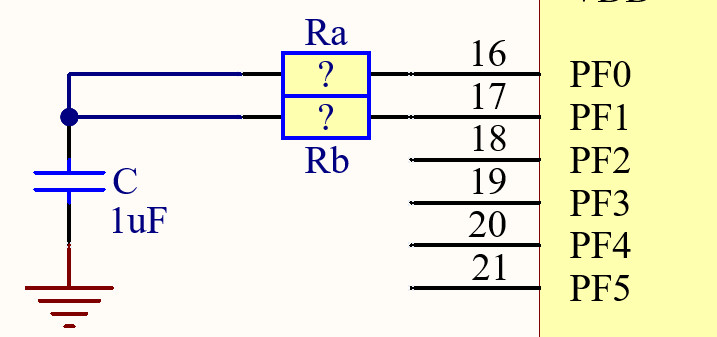
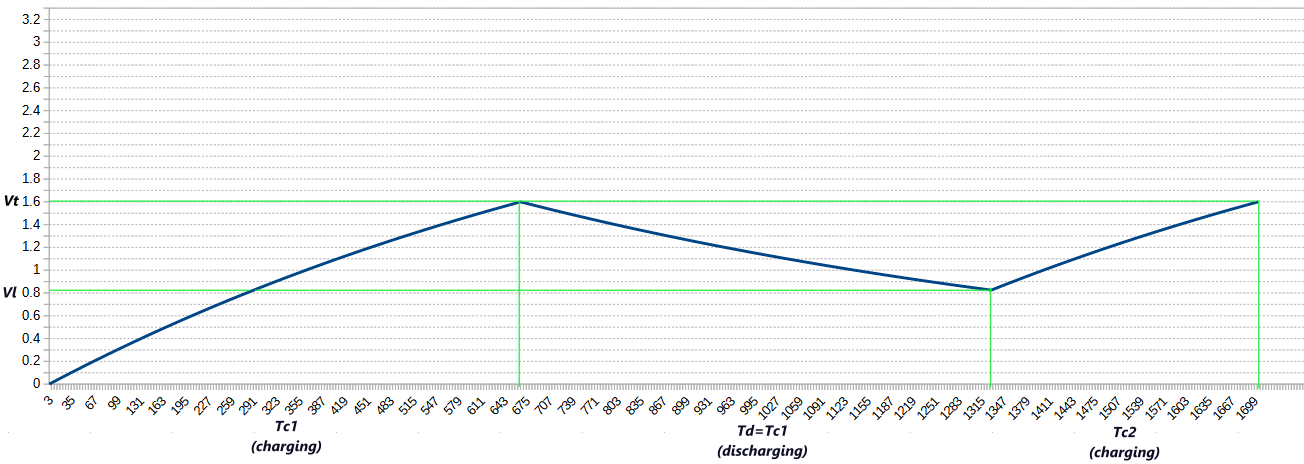
1. Completely discharge the capacitor (all pins are low)
2. Charge the capacitor until the voltage crosses the 0->1 voltage threshold (Vt) and measure the charging time #1 (Tc1).
3. Immediately discharge the capacitor to some unknown low voltage (Vl) - it should be well below the Vt threshold, using the same period of time used for charging as the discharge period (Td = Tc1).
4. Immediately charge the capacitor again and measure the time crossing the same 0->1 voltage threshold again (Tc2).
5. Repeat the procedure several times to get more precise timings.
6. Do some math and find the R and C values.
7. Board_Id = the unique combination of indices of the "measured" R1 and R2.

The math proof:

• Charging formula #1: Vt = Vcc * (1 - exp(-Tc1 / RC))

• Discharging formula: Vl = Vt * exp(-Td / RC)

• Charging formula #2: Vl = Vcc * (1 - exp(-Tl / (RC)))

• Where Tl is a charging time from 0 to Vl: Tl = Tc1 - Tc2

• Solve the equations: Vl = Vcc * (1 - exp(-Tl / RC)) = Vt * exp(-Td / RC)

  Vcc * (1 - exp(-Tl / RC)) = Vcc * (1 - exp(-Tc1 / RC)) * exp(-Td / RC)

  (1 - exp(-Tl / RC)) = (1 - exp(-Tc1 / RC)) * exp(-Td / RC)

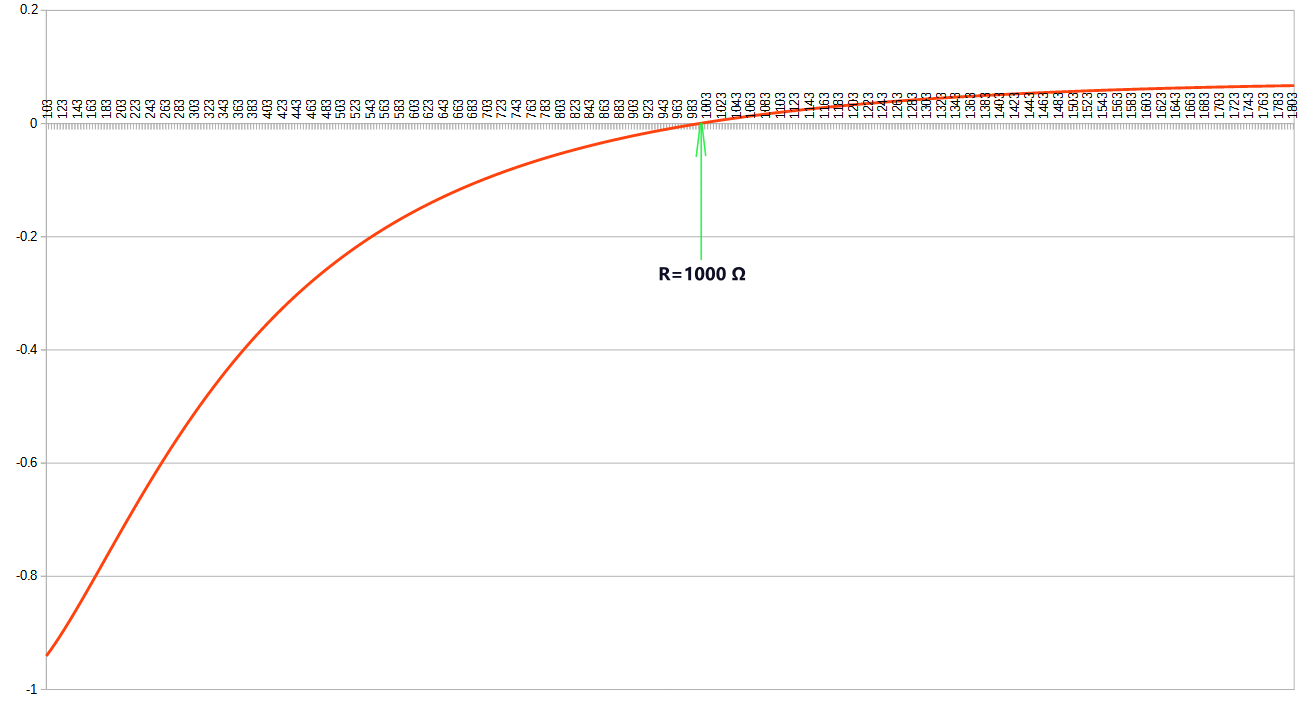
• Simplify the equation: X = exp(-1/(RC))

  (1 - X^Tc1) * X^Td + X^Tl - 1 = 0

  X^Td - X^(Tc1+Td) + X^(Tc2-Tc1) - 1 = 0

  Td, Tc1 and Tc2 are known.

• Solve the power function for X and get the desired R or C.

The solver:

We use Newton's method (a fast-converging numerical solver when the 1st derivative is known) with estimated initial values.