-
-
Notifications
You must be signed in to change notification settings - Fork 13
Advanced Particle Equations
Particle equations are one of the more powerful features of DragonEggDrop - Revival and has the potential to give server owners the utmost control over the particles displayed after the death of the dragon. Evidently, this feature was created for those more skilled in mathematics and the understanding of particles shapes (unlike myself). If you are capable of creating advanced particle equations, please do send them my way through the Issue Tracker with a video or gif of the animation and it may be added as a preset function much like HELIX or OPEN_END_HELIX.
In order to begin creating an equation, the Particles.Advanced.preset-shape configuration option must be set to CUSTOM. If this value is not set, the custom functions will not be parsed and will be ignored with the preset value instead.
When writing equations, it's worth noting that there are 3 very strict limitations.
- These equations are fixed on the x and z plains. You cannot modify the y coordinate
- The particles are constantly moving downwards
- There is no way to change the center of the particle effects. It will always center at 0.5, 0.5, (the center of the portal)
These rules will not change and must be kept in mind when writing equations. Variables may not be changed systematically which will be further explained in Supported Variables.
When writing a custom equation, one must be aware that there are 2 aspects to be wary of. The x and z axis contain separate equations to allow for maximum flexibility on each axis. The x axis affects the west and south directions whereas the z axis affects the north and south directions. To take advantage of these axises, it's best to work on these equations separately and tweak them based on their result. Take for example the default equations
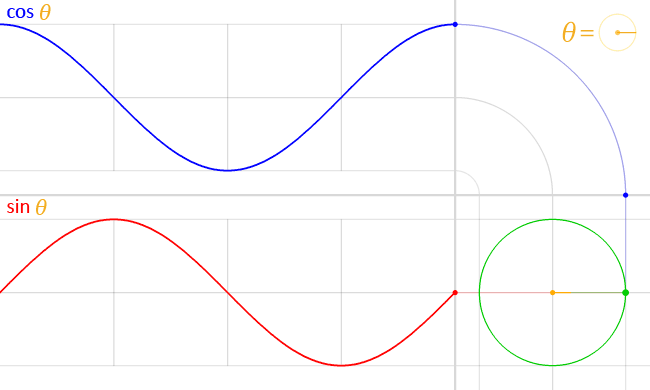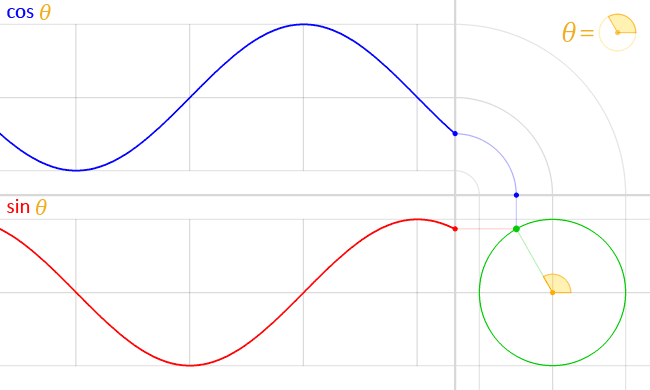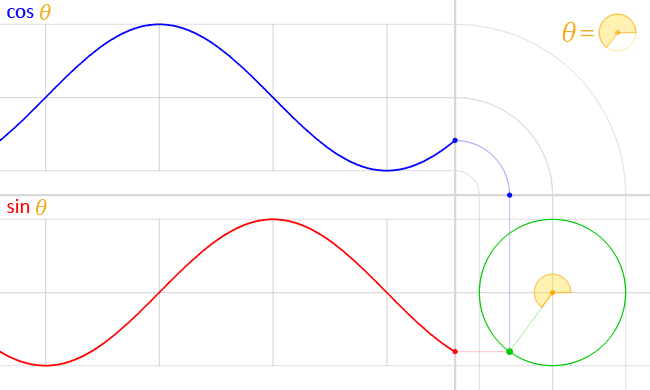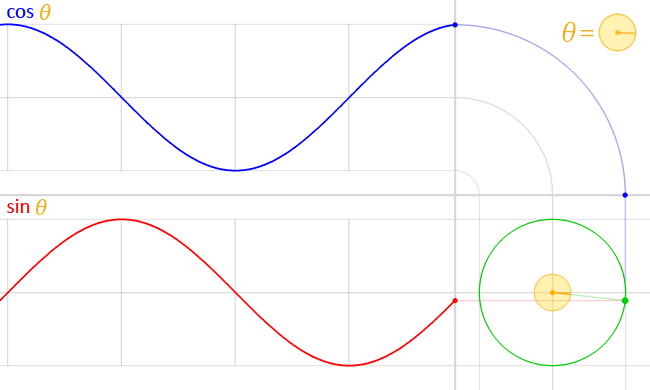
x-coord-expression: 'cos(theta)'
z-coord-expression: 'sin(theta)'
These are very clearly replicating the creation of a circle on a cartesian plane.
The above gif demonstrates how the expressions work together to create a circle but work independently from one another. Programmatically, these two equations are parsed and cached, and the result of the two equations are added together on each axis from the center to get a point. At that point is where the particle will be displayed for that tick. For example, assuming the center value of x = 0.5 and z = 0.5, if theta is at a value of 180, the resulting particle point would be x = -0.0984600691 (0.5 + cos(180)) and z = -0.301152636 (0.5 + sin(180)).
The equation parser comes with a set of predefined functions usable in any equation at any point. Functions may be used in the syntax of func(value) or funcvalue as exemplified above through the use of sin(theta) and cos(theta). Below is a table of all supported functions and their descriptions
| Function | Description | Example |
|---|---|---|
| sqrt | Square root a specified value | sqrt(25) ... results in 5 |
| abs | The absolute of a value | abs(-25) ... results in 25 |
| log | Log base 10 of a value | log(10) ... results in 1 |
| sin | The sine trigonometric function | sin(30) or sin30 ... results in 0.5 |
| cos | The cosine trigonometric function | cos(45) or cos45 ... results in 0.7071 |
| tan | The tan trigonometric function | tan(60) or tan60 ... results in 1.7320 |
| csc | The cosecant trigonometric function | csc(30) or csc30 ... results in -1.0121 |
| sec | The secant trigonometric function | sec(45) or sec45 ... results in 1.9035 |
| cot | The cotangent trigonometric function | cot(60) or cot60 ... results in 3.1246 |
| rad | Convert a value from degrees to radians | rad(180) ... results in 3.1415, or, pi |
| deg | Convert a value from radians to degrees | deg(6.2832) ... results in 360 |
In using the above functions, each will return a numerical value. When using them in an equation, imagine it returning a value. For example, executing 1 + abs(-1) will result in 2 as though abs(-1) was evaluated and re-parsed as a 1, its product.
In addition to functions, the parser also passes dynamic variables which may be used to manipulate the function based on its current time or an accumulating value of theta. These variables may be used anywhere in the equation, including as values passed to functions! As exemplified in the default equation, theta is used in both sin and cos functions to return different values.
| Variable | Description | Possible Values |
|---|---|---|
| x | The x coordinate of the particles | Typically, unless modified, this is set to 0.5 |
| z | The z coordinate of the particles | Typically, unless modified, this is set to 0.5 |
| t | The current time position of the animation | Starting at 0, incremented 1 every iteration |
| theta | A placeholder for theta (in degrees) | Starting at 0 degrees, incremented 5 every iteration |
To use the above variables, simply write them into the equation at any time. If the value if modified in the equation said modification is not reflected in the system. For example, if t = 1 and the equation is abs(t + 1), the variable t will be incremented for the function and will return 2. However, upon its next iteration, t = 2 and will increment as per usual. The function will now return 3.