##Python中list 的实现
原文链接
这篇文章介绍了Python中list是如何实现的。
在Python中list特别有用。让我们来看下list的内部是如何实现的。
来看下面简单的程序,在list中添加一些整数并将他们打印出来。
>>> L = []
>>> L.append(1)
>>> L.append(2)
>>> L.append(3)
>>> L
[1, 2, 3]
>>> for e in L:
... print e
...
1
2
3
正如你所看到的,list是可以迭代的。
###List对象的C结构
Python中list是用下边的C语言的结构来表示的。ob_item是用来保存元素的指针数组,allocated是ob_item预先分配的内存总容量
typedef struct {
PyObject_VAR_HEAD
PyObject **ob_item;
Py_ssize_t allocated;
} PyListObject;
###List的初始化 让我们来看下当初始化一个空list的时候发生了什么 L = []
arguments: size of the list = 0
returns: list object = []
PyListNew:
nbytes = size * size of global Python object = 0
allocate new list object
allocate list of pointers (ob_item) of size nbytes = 0
clear ob_item
set list's allocated var to 0 = 0 slots
return list object
非常重要的是知道list申请内存空间的大小(后文用allocated代替)的大小和list实际存储元素所占空间的大小(ob_size)之间的关系,ob_size的大小和len(L)是一样的,而allocated的大小是在内存中已经申请空间大小。通常你会看到allocated的值要比ob_size的值要大。这是为了避免每次有新元素加入list时都要调用realloc进行内存分配。接下来我们会看到更多关于这些的内容。 ###Append 我们在list中追加一个整数:L.append(1)。发生了什么?调用了内部的C函数app1()
arguments: list object, new element
returns: 0 if OK, -1 if not
app1:
n = size of list
call list_resize() to resize the list to size n+1 = 0 + 1 = 1
list[n] = list[0] = new element
return 0
来让我们看下list_resize()。list_resize()会申请多余的空间以避免调用多次list_resize()函数,list增长的模型是:0, 4, 8, 16, 25, 35, 46, 58, 72, 88, …
arguments: list object, new size
returns: 0 if OK, -1 if not
list_resize:
new_allocated = (newsize >> 3) + (newsize < 9 ? 3 : 6) = 3
new_allocated += newsize = 3 + 1 = 4
resize ob_item (list of pointers) to size new_allocated
return 0
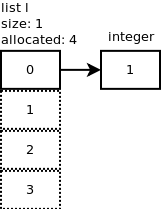
开辟了四个内存空间来存放list中的元素,存放的第一个元素是1。你可以从下图中看到L[0]指向了我们刚刚加进去的元素。虚线的框代表了申请了但是还没有使用(存储元素)的内存空间
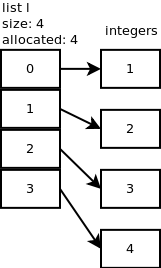
我们继续加入一个元素:L.append(2)。调用list_resize,同时n+1=2。但是因为allocated(译者注:已经申请的空间大小)是4。所以没有必要去申请新的内存空间。相同的事情发生在再次在list中添加两个元素的时候:L.append(3),L.append(4)。下图展示了到目前为止我们做了什么。
###Insert
现在我们在列表的第一个位置插入一个整数5:L.insert(1, 5),看看内部发生了什么。调用了ins1()
arguments: list object, where, new element
returns: 0 if OK, -1 if not
ins1:
resize list to size n+1 = 5 -> 4 more slots will be allocated
starting at the last element up to the offset where, right shift each element
set new element at offset where
return 0
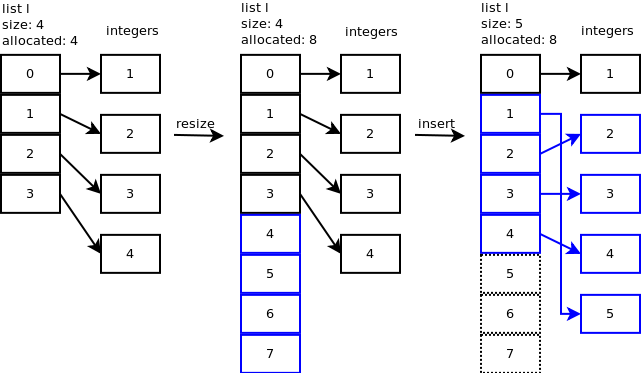
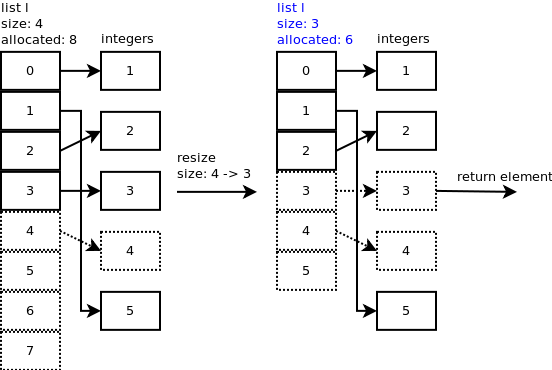
虚线框表示已经申请但是没有使用的内存。申请了8个内存空间但是list实际用来存储元素只使用了其中5个内存空间
insert的时间复杂度是O(n)
###Pop
当你弹出list的最后一个元素:L.pop()。调用listpop(),list_resize在函数listpop()内部被调用,如果这时ob_size(译者注:弹出元素后)小于allocated(译者注:已经申请的内存空间)的一半。这时申请的内存空间将会缩小。
arguments: list object
returns: element popped
listpop:
if list empty:
return null
resize list with size 5 - 1 = 4. 4 is not less than 8/2 so no shrinkage
set list object size to 4
return last element
Pop的时间复杂度是O(1)
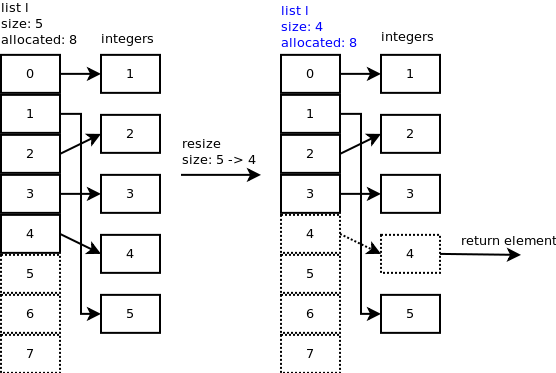
你可以发现4号内存空间指向还指向那个数值(译者注:弹出去的那个数值),但是很重要的是ob_size现在却成了4.
让我们再弹出一个元素。在list_resize内部,size – 1 = 4 – 1 = 3 比allocated(已经申请的空间)的一半还要小。所以list的申请空间缩小到6个,list的实际使用空间现在是3个(译者注:根据(newsize >> 3) + (newsize < 9 ? 3 : 6) = 3在文章最后有详述)
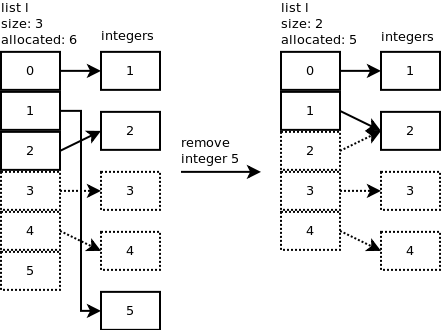
你可以发现(下图)3号和4号内存空间还存储着一些整数,但是list的实际使用(存储元素)空间却只有3个了。
###Remove
Python list对象有一个方法可以移除一个指定的元素。调用listremove()。
arguments: list object, element to remove
returns none if OK, null if not
listremove:
loop through each list element:
if correct element:
slice list between element's slot and element's slot + 1
return none
return null
切开list和删除元素,调用了list_ass_slice()(译者注:在上文slice list between element's slot and element's slot + 1被调用),来看下list_ass_slice()是如何工作的。在这里,低位为1 高位为2(译者注:传入的参数),我们移除在1号内存空间存储的数据5
arguments: list object, low offset, high offset
returns: 0 if OK
list_ass_slice:
copy integer 5 to recycle list to dereference it
shift elements from slot 2 to slot 1
resize list to 5 slots
return 0
###Sort
下面以包含130个元素的list为例说明排序算法。如果list元素个数少于64,用折半插入排序足以进行快速排序,如果元素个数大于64,则需要进行归并排序。
下面这段程序创建了一个元素范围从0到129的list,并随机排列。
>>> import random
>>> l = [n for n in range(130)]
>>> random.shuffle(l)
>>> l
[107, 44, 97, 121, 26, 11, 24, 100, 79, 19, 109, 7, 52, 93, 70, 94, 124, 117, 92, 32, 115, 83, 9, 112, 84, 22, 65, 95, 89, 74, 64, 23, 101, 68, 119, 127, 90, 80, 91, 75, 4, 20, 114, 16, 103, 34, 96, 125, 47, 77, 81, 3, 30, 14, 25, 29, 104, 102, 98, 69, 78, 60, 33, 12, 31, 37, 76, 10, 5, 105, 35, 48, 85, 106, 63, 71, 54, 39, 8, 6, 62, 67, 42, 72, 118, 116, 27, 46, 38, 99, 126, 40, 28, 113, 43, 41, 59, 2, 56, 61, 88, 18, 45, 128, 58, 73, 1, 13, 129, 49, 0, 82, 123, 111, 57, 86, 110, 51, 15, 36, 120, 108, 66, 55, 53, 87, 122, 17, 21, 50]
第一步是寻找其中的自然有序列,例如: l[i] <= l[i+1] <= ... 或者 l[i] > l[i+1] > … 由于例子里的list随机排序, 自然有序列是比较少的。 这里我们还需要基于list长度给出的自然有序列最小长度。函数merge_compute_minrun() 将根据list的长度返回有序列的最小长度。 在本例中, 最短有序列长度为33。 对于长度小于33的自然有序列,我们用折半插入排序法将其延展为长度33的有序列。
本例中,l[0] >= l[1],但是l[2] > l[1],所以我们的第一个自然有序列是2,有些过短,但对于一个随机排序列来说也属正常。在实际运用中,自然有序列会更常见,从而使我们的排序算法比应用在这个例子上更有效率。
第一个自然有序列长度为2,所以我们用折半插入排序将其扩展到32个元素,之后再用归并法的结构管理不同列。 做完排序的第一个自然有序列包括从l[0]到l[32]的元素,如下: [7, 9, 11, 19, 22, 23, 24, 26, 32, 44, 52, 64, 65, 70, 74, 79, 83, 84, 89, 92, 93, 94, 95, 97, 100, 101, 107, 109, 112, 115, 117, 121, 124].
现在接着从l[33]开始考虑,得到长度为3的自然有序列: l[33] < l[34] < l[35],于是再次运动折半插入排序得到第2个排序列: [3, 4, 12, 14, 16, 20, 25, 29, 30, 31, 33, 34, 37, 47, 60, 68, 69, 75, 77, 78, 80, 81, 90, 91, 96, 98, 102, 103, 104, 114, 119, 125, 127].
同样方法我们得到长度为33的第3列和长度为31的第4列:
第一列: [7, 9, 11, 19, 22, 23, 24, 26, 32, 44, 52, 64, 65, 70, 74, 79, 83, 84, 89, 92, 93, 94, 95, 97, 100, 101, 107, 109, 112, 115, 117, 121, 124] 第二列: [3, 4, 12, 14, 16, 20, 25, 29, 30, 31, 33, 34, 37, 47, 60, 68, 69, 75, 77, 78, 80, 81, 90, 91, 96, 98, 102, 103, 104, 114, 119, 125, 127] 第三列: [2, 5, 6, 8, 10, 27, 28, 35, 38, 39, 40, 41, 42, 43, 46, 48, 54, 56, 59, 62, 63, 67, 71, 72, 76, 85, 99, 105, 106, 113, 116, 118, 126] 第四列: [0, 1, 13, 15, 17, 18, 21, 36, 45, 49, 50, 51, 53, 55, 57, 58, 61, 66, 73, 82, 86, 87, 88, 108, 110, 111, 120, 122, 123, 128, 129]
接下来进行归并,不同列持续归并直到最后得到长度为130的一列。
首先归并第一列和第二列,归并算法比较复杂,运用gallop的概念加速排序。 如果在归并过程中,同一列多于7个元素被选中,则进入gallop模式,一系列区间被移动到归并暂时存储区域,而不是继续进行一对一的传统比较。关于galloping模式的更多细节请参见listsort.txt。总之,排序完成后,我们得到了66个元素的一个有序列: [3, 4, 7, 9, 11, 12, 14, 16, 19, 20, 22, 23, 24, 25, 26, 29, 30, 31, 32, 33, 34, 37, 44, 47, 52, 60, 64, 65, 68, 69, 70, 74, 75, 77, 78, 79, 80, 81, 83, 84, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 100, 101, 102, 103, 104, 107, 109, 112, 114, 115, 117, 119, 121, 124, 125, 127]
接下来我们将这个66个元素的有序列和原先的第三列归并,得到一个99个元素的有序列: [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 16, 19, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 37, 38, 39, 40, 41, 42, 43, 44, 46, 47, 48, 52, 54, 56, 59, 60, 62, 63, 64, 65, 67, 68, 69, 70, 71, 72, 74, 75, 76, 77, 78, 79, 80, 81, 83, 84, 85, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 109, 112, 113, 114, 115, 116, 117, 118, 119, 121, 124, 125, 126, 127]
最后再和第四列归并得到130个元素的有序列,也就是最终结果: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129]
排序时间复杂度为 O(n log n).
核心部分
我们能看到 Python 设计者的苦心。在需要的时候扩容,但又不允许过度的浪费,适当的内存回收是非常必要的。
这个确定调整后的空间大小算法很有意思。
调整后大小 (new_allocated) = 新元素数量 (newsize) + 预留空间 (new_allocated)
调整后的空间肯定能存储 newsize 个元素。要关注的是预留空间的增长状况。
将预留算法改成 Python 版就更清楚了:(newsize // 8) + (newsize < 9 and 3 or 6)。
当 newsize >= allocated,自然按照这个新的长度 "扩容" 内存。
而如果 newsize < allocated,且利用率低于一半呢?
allocated newsize new_size + new_allocated
10 4 4 + 3
20 9 9 + 7
很显然,这个新长度小于原来的已分配空间长度,自然会导致 realloc 收缩内存。(不容易啊)
引自《深入Python编程》