Recap: Haskell Crash Course II
+
-
+
- Core program element is an expression +
- Every valid expression has a type (determined at compile-time) +
- Every valid expression reduces to a value (computed at run-time) +
+
+
+
+
+
+
+
+
Recap: Haskell
+Basic values & operators
+-
+
Int,Bool,Char,Double
++,-,==,/=
+
Execution / Function Calls
+-
+
- Just substitute equals by equals +
Producing Collections
+-
+
- Pack data into tuples & lists +
Consuming Collections
+-
+
- Unpack data via pattern-matching +
+
+
+
+
+
+
+
+
Next: Creating and Using New Data Types
+-
+
typeSynonyms: Naming existing types
+datatypes: Creating new types
+
+
+
+
+
+
+
+
+
Type Synonyms
+Synonyms are just names (“aliases”) for existing types
+-
+
- think
typedefinC
+
+
+
+
+
+
+
+
+
A type to represent Circle
+A tuple (x, y, r) is a circle with center at (x, y) and radius r
type Circle = (Double, Double, Double)
+
+
+
+
+
+
+
+
+
A type to represent Cuboid
+A tuple (length, depth, height) is a cuboid
type Cuboid = (Double, Double, Double)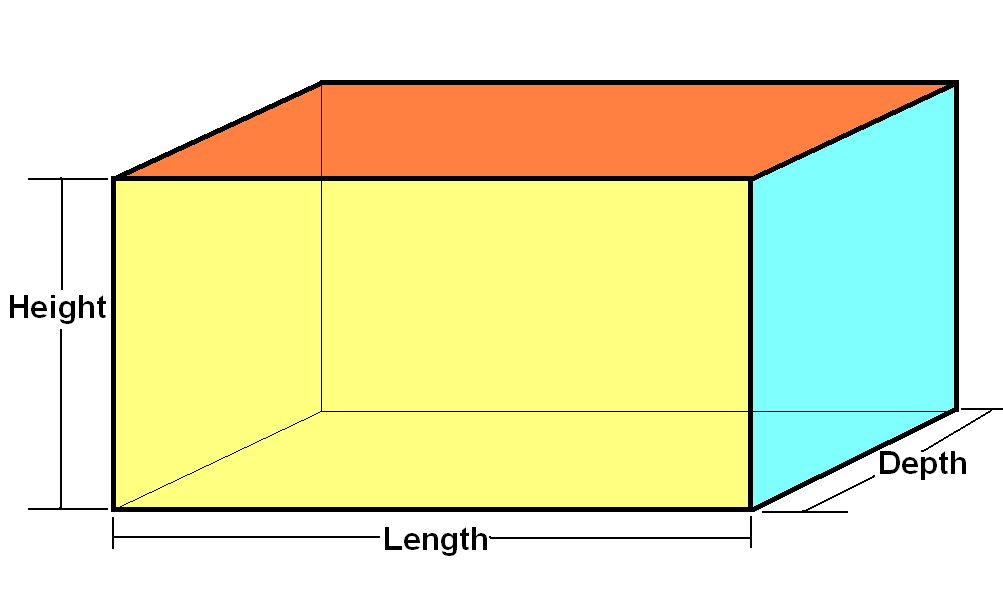
+
+
+
+
+
+
+
+
Using Type Synonyms
+We can now use synonyms by creating values of the given types
+circ0 :: Circle
+circ0 = (0, 0, 100) -- ^ circle at "origin" with radius 100
+
+cub0 :: Cuboid
+cub0 = (10, 20, 30) -- ^ cuboid with length=10, depth=20, height=30 And we can write functions over synonyms too
+area :: Circle -> Double
+area (x, y, r) = pi * r * r
+
+volume :: Cuboid -> Double
+volume (l, d, h) = l * d * h We should get this behavior
+>>> area circ0
+31415.926535897932
+
+>>> volume cub0
+6000
+
+
+
+
+
+
+
+
QUIZ
+Suppose we have the definitions
+type Circle = (Double, Double, Double)
+type Cuboid = (Double, Double, Double)
+
+circ0 :: Circle
+circ0 = (0, 0, 100) -- ^ circle at "origin" with radius 100
+
+cub0 :: Cuboid
+cub0 = (10, 20, 30) -- ^ cuboid with length=10, depth=20, height=30
+
+area :: Circle -> Double
+area (x, y, r) = pi * r * r
+
+volume :: Cuboid -> Double
+volume (l, d, h) = l * d * hWhat is the result of
+>>> volume circ0A. 0
B. Type error
+
+
+
+
+
+
+
+
+
Beware!
+Type Synonyms
+-
+
Do not create new types
+Just name existing types
+
And hence, synonyms
+-
+
- Do not prevent confusing different values +
+
+
+
+
+
+
+
+
Creating New Data Types
+We can avoid mixing up by creating new data types
-- | A new type `CircleT` with constructor `MkCircle`
+data CircleT = MkCircle Double Double Double
+
+-- | A new type `CuboidT` with constructor `MkCuboid`
+data CuboidT = MkCuboid Double Double DoubleConstructors are the only way to create values
+-
+
MkCirclecreatesCircleT
+MkCuboidcreatesCuboidT
+
+
+
+
+
+
+
+
+
QUIZ
+Suppose we create a new type with a data definition
-- | A new type `CircleT` with constructor `MkCircle`
+data CircleT = MkCircle Double Double Double What is the type of the MkCircle constructor?
A. MkCircle :: CircleT
B. MkCircle :: Double -> CircleT
C. MkCircle :: Double -> Double -> CircleT
D. MkCircle :: Double -> Double -> Double -> CircleT
E. MkCircle :: (Double, Double, Double) -> CircleT
+
+
+
+
+
+
+
+
Constructing Data
+Constructors let us build values of the new type
+circ1 :: CircleT
+circ1 = MkCircle 0 0 100 -- ^ circle at "origin" w/ radius 100
+
+cub1 :: Cuboid
+cub1 = MkCuboid 10 20 30 -- ^ cuboid w/ len=10, dep=20, ht=30
+
+
+
+
+
+
+
+
QUIZ
+Suppose we have the definitions
+data CuboidT = MkCuboid Double Double Double
+
+type Cuboid = (Double, Double, Double)
+
+volume :: Cuboid -> Double
+volume (l, d, h) = l * d * hWhat is the result of
+>>> volume (MkCuboid 10 20 30)A. 6000
B. Type error
+
+
+
+
+
+
+
+
+
Deconstructing Data
+Constructors let us build values of new type … but how to use those values?
+How can we implement a function
+volume :: Cuboid -> Double
+volume c = ???such that
+>>> volume (MkCuboid 10 20 30)
+6000
+
+
+
+
+
+
+
+
Deconstructing Data by Pattern Matching
+Haskell lets us deconstruct data via pattern-matching
+volume :: Cuboid -> Double
+volume c = case c of
+ MkCuboid l d h -> l * d * hcase e of Ctor x y z -> e1 is read as as
IF
+- e evaluates to a value that matches the pattern Ctor vx vy vz
THEN
+- evaluate e1 after naming x := vx, y := vy, z := vz
+
+
+
+
+
+
+
+
Pattern matching on Function Inputs
+Very common to do matching on function inputs
+volume :: Cuboid -> Double
+volume c = case c of
+ MkCuboid l d h -> l * d * h
+
+area :: Circle -> Double
+area a = case a of
+ MkCircle x y r -> pi * r * rSo Haskell allows a nicer syntax: patterns in the arguments
+volume :: Cuboid -> Double
+volume (MkCuboid l d h) = l * d * h
+
+area :: Circle -> Double
+area (MkCircle x y r) = pi * r * rNice syntax plus the compiler saves us from mixing up values!
+
+
+
+
+
+
+
+
+
But … what if we need to mix up values?
+Suppose I need to represent a list of shapes
+-
+
- Some
Circles
+ - Some
Cuboids
+
What is the problem with shapes as defined below?
shapes = [circ1, cub1]Where we have defined
+circ1 :: CircleT
+circ1 = MkCircle 0 0 100 -- ^ circle at "origin" with radius 100
+
+cub1 :: Cuboid
+cub1 = MkCuboid 10 20 30 -- ^ cuboid with length=10, depth=20, height=30
+
+
+
+
+
+
+
+
Problem: All list elements must have the same type
+Solution???
+
+
+
+
+
+
+
+
+
+
QUIZ: Variant (aka Union) Types
+Lets create a single type that can represent both kinds of shapes!
+data Shape
+ = MkCircle Double Double Double -- ^ Circle at x, y with radius r
+ | MkCuboid Double Double Double -- ^ Cuboid with length, depth, heightWhat is the type of MkCircle 0 0 100 ?
A. Shape
B. Circle
C. (Double, Double, Double)
+
+
+
+
+
Each Data Constructor of Shape has a different type
+When we define a data type like the below
+data Shape
+ = MkCircle Double Double Double -- ^ Circle at x, y with radius r
+ | MkCuboid Double Double Double -- ^ Cuboid with length, depth, heightWe get multiple constructors for Shape
MkCircle :: Double -> Double -> Double -> Shape
+MkCuboid :: Double -> Double -> Double -> ShapeNow we can create collections of Shape
+Now we can define
+circ2 :: Shape
+circ2 = MkCircle 0 0 100 -- ^ circle at "origin" with radius 100
+
+cub2 :: Shape
+cub2 = MkCuboid 10 20 30 -- ^ cuboid with length=10, depth=20, height=30 and then define collections of Shapes
shapes :: [Shape]
+shapes = [circ1, cub1]
+
+
+
+
+
EXERCISE
+Lets define a type for 2D shapes
+data Shape2D
+ = MkRect Double Double -- ^ 'MkRect w h' is a rectangle with width 'w', height 'h'
+ | MkCirc Double -- ^ 'MkCirc r' is a circle with radius 'r'
+ | MkPoly [Vertex] -- ^ 'MkPoly [v1,...,vn]' is a polygon with vertices at 'v1...vn'
+
+type Vertex = (Double, Double)Write a function to compute the area of a Shape2D
area2D :: Shape2D -> Double
+area2D s = ???HINT
+ +
+
+
+You may want to use this helper that computes the area of a triangle at v1, v2, v3
areaTriangle :: Vertex -> Vertex -> Vertex -> Double
+areaTriangle v1 v2 v3 = sqrt (s * (s - s1) * (s - s2) * (s - s3))
+ where
+ s = (s1 + s2 + s3) / 2
+ s1 = distance v1 v2
+ s2 = distance v2 v3
+ s3 = distance v3 v1
+
+distance :: Vertex -> Vertex -> Double
+distance (x1, y1) (x2, y2) = sqrt ((x2 - x1) ** 2 + (y2 - y1) ** 2)
+
+
+
+
+
+
+
+
+
Polymorphic Data Structures
+Next, lets see polymorphic data types
+which contain many kinds of values.
+
+
+
+
+
+
+
+
+
+
Recap: Data Types
+Recall that Haskell allows you to create brand new data types
+data Shape
+ = MkRect Double Double
+ | MkPoly [(Double, Double)]
+
+
+
+
+
+
+
+
+
QUIZ
+What is the type of MkRect ?
data Shape
+ = MkRect Double Double
+ | MkPoly [(Double, Double)]a. Shape
b. Double
c. Double -> Double -> Shape
d. (Double, Double) -> Shape
e. [(Double, Double)] -> Shape
+
+
+
+
+
+
+
+
+
Tagged Boxes
+Values of this type are either two doubles tagged with Rectangle
>>> :type (Rectangle 4.5 1.2)
+(Rectangle 4.5 1.2) :: Shapeor a list of pairs of Double values tagged with Polygon
ghci> :type (Polygon [(1, 1), (2, 2), (3, 3)])
+(Polygon [(1, 1), (2, 2), (3, 3)]) :: ShapeData values inside special Tagged Boxes
+ +
+
+
+
+
+
+
+
+
+
+
+
+
Recursive Data Types
+We can define datatypes recursively too
+data IntList
+ = INil -- ^ empty list
+ | ICons Int IntList -- ^ list with "hd" Int and "tl" IntList
+ deriving (Show)(Ignore the bit about deriving for now.)
+
+
+
+
+
+
+
+
+
QUIZ
+data IntList
+ = INil -- ^ empty list
+ | ICons Int IntList -- ^ list with "hd" Int and "tl" IntList
+ deriving (Show)What is the type of ICons ?
A. Int -> IntList -> List
B. IntList
C. Int -> IntList -> IntList
D. Int -> List -> IntList
E. IntList -> IntList
+
+
+
+
+
+
+
+
+
Constructing IntList
+Can only build IntList via constructors.
>>> :type INil
+INil:: IntList
+
+>>> :type ICons
+ICons :: Int -> IntList -> IntList
+
+
+
+
+
+
+
+
+
EXERCISE
+Write down a representation of type IntList of the list of three numbers 1, 2 and 3.
list_1_2_3 :: IntList
+list_1_2_3 = ???Hint Recursion means boxes within boxes
+ +
+
+
+
+
+
+
+
+
+
+
+
+
Trees: Multiple Recursive Occurrences
+We can represent Int trees like
data IntTree
+ = ILeaf Int -- ^ single "leaf" w/ an Int
+ | INode IntTree IntTree -- ^ internal "node" w/ 2 sub-trees
+ deriving (Show)A leaf is a box containing an Int tagged ILeaf e.g.
>>> it1 = ILeaf 1
+>>> it2 = ILeaf 2A node is a box containing two sub-trees tagged INode e.g.
>>> itt = INode (ILeaf 1) (ILeaf 2)
+>>> itt' = INode itt itt
+>>> INode itt' itt'
+INode (INode (ILeaf 1) (ILeaf 2)) (INode (ILeaf 1) (ILeaf 2))
+
+
+
+
+
+
+
+
+
Multiple Branching Factors
+e.g. 2-3 trees
+data Int23T
+ = ILeaf0
+ | INode2 Int Int23T Int23T
+ | INode3 Int Int23T Int23T Int23T
+ deriving (Show)An example value of type Int23T would be
i23t :: Int23T
+i23t = INode3 0 t t t
+ where t = INode2 1 ILeaf0 ILeaf0which looks like
+ +
+
+
+
+
+
+
+
+
+
+
+
+
Parameterized Types
+We can define CharList or DoubleList
+- versions of IntList for Char and Double as
data CharList
+ = CNil
+ | CCons Char CharList
+ deriving (Show)
+
+data DoubleList
+ = DNil
+ | DCons Char DoubleList
+ deriving (Show)
+
+
+
+
+
+
+
+
+
Don’t Repeat Yourself!
+Don’t repeat definitions +- Instead reuse the list structure across all types!
+Find abstract data patterns by
+-
+
- identifying the different parts and +
- refactor those into parameters +
+
+
+
+
+
+
A Refactored List
+Here are the three types: What is common? What is different?
+data IList = INil | ICons Int IList
+
+data CList = CNil | CCons Char CList
+
+data DList = DNil | DCons Double DListCommon: Nil/Cons structure
Different: type of each “head” element
+Refactored using Type Parameter
+data List a = Nil | Cons a (List a)Recover original types as instances of List
+type IntList = List Int
+type CharList = List Char
+type DoubleList = List Double
+
+
+
+
+
+
+
+
+
+
+
+
+
Polymorphic Data has Polymorphic Constructors
+Look at the types of the constructors
+>>> :type Nil
+Nil :: List aThat is, the Empty tag is a value of any kind of list, and
>>> :type Cons
+Cons :: a -> List a -> List aCons takes an a and a List a and returns a List a.
cList :: List Char -- list where 'a' = 'Char'
+cList = Cons 'a' (Cons 'b' (Cons 'c' Nil))
+
+iList :: List Int -- list where 'a' = 'Int'
+iList = Cons 1 (Cons 2 (Cons 3 Nil))
+
+dList :: List Double -- list where 'a' = 'Double'
+dList = Cons 1.1 (Cons 2.2 (Cons 3.3 Nil))
+
+
+
+
+
+
+
+
+
+
+
+
+
Polymorphic Function over Polymorphic Data
+Lets write the list length function
+len :: List a -> Int
+len Nil = 0
+len (Cons x xs) = 1 + len xslen doesn’t care about the actual values in the list
+- only “counts” the number of Cons constructors
Hence len :: List a -> Int
-
+
- we can call
lenon any kind of list.
+
>>> len [1.1, 2.2, 3.3, 4.4] -- a := Double
+4
+
+>>> len "mmm donuts!" -- a := Char
+11
+
+>>> len [[1], [1,2], [1,2,3]] -- a := ???
+3
+
+
+
+
+
+
+
+
+
+
+
+
+
Built-in Lists?
+This is exactly how Haskell’s “built-in” lists are defined:
+data [a] = [] | (:) a [a]
+
+data List a = Nil | Cons a (List a)-
+
Nilis called[]
+Consis called:
+
Many list manipulating functions e.g. in Data.List are polymorphic +- Can be reused across all kinds of lists.
+(++) :: [a] -> [a] -> [a]
+head :: [a] -> a
+tail :: [a] -> [a]
+
+
+
+
+
+
+
+
+
+
+
+
+
Generalizing Other Data Types
+Polymorphic trees
+data Tree a
+ = Leaf a
+ | Node (Tree a) (Tree a)
+ deriving (Show)Polymorphic 2-3 trees
+data Tree23 a
+ = Leaf0
+ | Node2 (Tree23 a) (Tree23 a)
+ | Node3 (Tree23 a) (Tree23 a) (Tree23 a)
+ deriving (Show)
+
+
+
+
+
+
+
+
+
+
+
+
+
Kinds
+List a corresponds to lists of values of type a.
If a is the type parameter, then what is List?
A type-constructor that
+- takes as input a type a
+- returns as output the type List a
But wait, if List is a type-constructor then what is its “type”?
-
+
- A kind is the “type” of a type. +
>>> :kind Int
+Int :: *
+>>> :kind Char
+Char :: *
+>>> :kind Bool
+Bool :: *Thus, List is a function from any “type” to any other “type”, and so
>>> :kind List
+List :: * -> *
+
+
+
+
+
+
+
+
+
+
+
+
+
QUIZ
+What is the kind of ->? That, is what does GHCi say if we type
>>> :kind (->) A. *
B. * -> *
C. * -> * -> *
We will not dwell too much on this now.
+As you might imagine, they allow for all sorts of abstractions over data.
+If interested, see this for more information about kinds.
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
 +
+