diff --git a/doc/modeling/implementation.md b/doc/modeling/implementation.md
index 51d8cfb0d..2e308a71a 100644
--- a/doc/modeling/implementation.md
+++ b/doc/modeling/implementation.md
@@ -83,7 +83,7 @@ This components are placed under the node named « topoLines_cath » and allow t
This component is one of the main important to simulate interventional radiology instruments. It inherits from the class adapt the parameters of the simulation.
- +
+
- angleMax: gives the maximum angle of bending of the catheter
@@ -163,7 +163,7 @@ Inside the component, the geometric support of each beams is a cubic spline. Fro
### AdaptiveBeamForceFieldAndMass
This component computes the Force and the mass using a beam formulation. The computation is based on a « corotational approach ».
- +
+
From the two 6DOF position of the nodes of the beam, we extract 4 points for defining a spline. Using this spline, we can find one central frame for the beam (in red in the figure). There is only one rotation that is not determined (along the axis of the spline). To find this twiting orientation, we use a slerp.
@@ -229,7 +229,7 @@ In the opposite direction, the Mapping also allows to transfer the forces and th
The hypothesis of beam FEM is based on interpolation function. This why this MultiAdpativeBeamMapping will rely on the interpolation defined in the WireBeamInterpolations. However, for the specific case of catheter instruments, several concentric instruments can be inserted. Then the mapping has to be done with the good interpolation functions
- +
+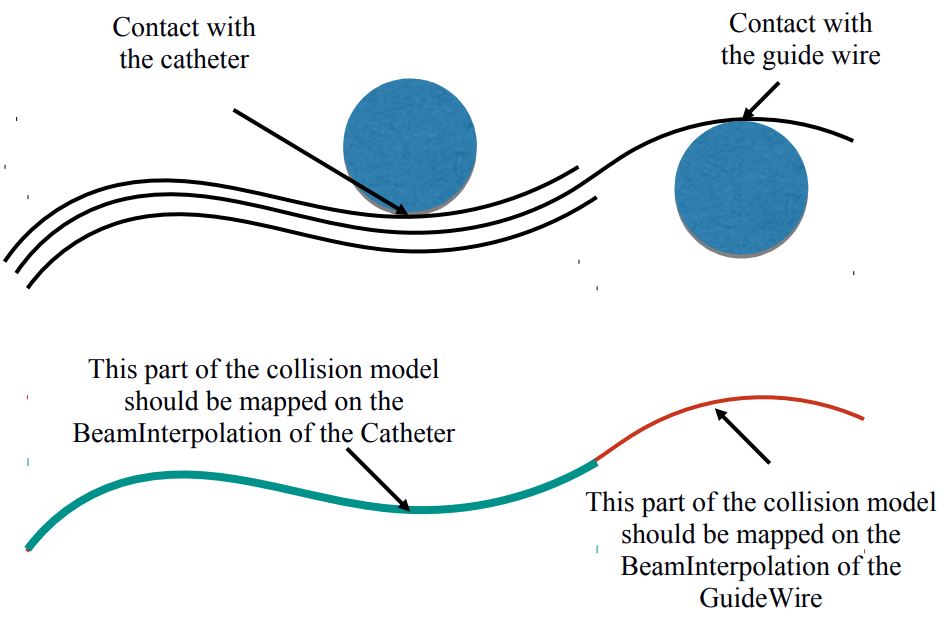
Consequently the MultiAdaptiveBeamMapping is directly « controlled » by the InterventionalRadiologyController and has to be linked to this component
diff --git a/doc/modeling/theory.md b/doc/modeling/theory.md
index 1ff5566c9..3e19206bf 100644
--- a/doc/modeling/theory.md
+++ b/doc/modeling/theory.md
@@ -17,12 +17,12 @@ rod or beam, we use a representation based on three-dimensional beam theory *see
elementary stiffness matrix Ke is a 12 × 12 symmetric matrix that relates angular and spacial positions of each end
of a beam element to the forces and torques applied to them:
- +
+
parameters:
-
+
The assumption of the corotational model is that the deformations remain ”small” at the level of each element.
@@ -41,7 +41,7 @@ We need a matrix relationship between the variation of the position δ **u** in
δ **q** in the global coordinates.
- +
+
This relationship is expressed by the matrix equation:
@@ -92,7 +92,7 @@ The description of the shape function relies on:
## WireRestShape
This component allows to define the rest shape of Wire instrument such as a catheter (modeled with a set of beams), the numerical parameters used in the simulation, and the topology used for the visualisation.
- +
+
Several physical and geometry parameters can be defined using SOFA Data such as the **densityOfBeams**, **straightLength**, **youngModulus**, **numEdges**, etc. See [implementation documentation](https://github.com/sofa-framework/BeamAdapter/blob/master/doc/modeling/implementation.md) for the full list.
@@ -105,7 +105,7 @@ This component is one of the most important in the modeling of catheter devices:
This component computes the Force and the mass using a beam formulation. The computation is based on a « corotational approach ».
- +
+
From the two 6DOF position of the nodes of the beam, we extract 4 points for defining a spline. Using this spline, we can find one central frame for the beam (in red in the figure). There is only one rotation that is not determined (along the axis of the spline). To find this twiting orientation, we use a slerp. The computation of the deformations of the beams are done in this frame and suppose linear deformations using beam elements (Timoshenko beams) .
@@ -115,7 +115,7 @@ From the two 6DOF position of the nodes of the beam, we extract 4 points for def
This mapping allows to drive the Mechanical Object of the collision object thanks to the position and velocity of the Mechanical Object of the parent node. In the opposite direction, the Mapping also allows to transfer the forces and the constraints from the collision model to the DOFs (the nodes of the beam).
The hypothesis of beam FEM is based on interpolation function. This why this MultiAdpativeBeamMapping will rely on the interpolation defined in the WireBeamInterpolations. However, for the specific case of catheter instruments, several concentric instruments can be inserted. Then the mapping has to be done with the good interpolation functions
- +
+
 +
+
 +
+
 +
+
 +
+


 +
+
 +
+
 +
+
 +
+