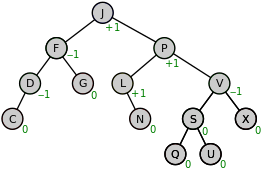
An avl tree is a specific type of binary search tree that automatically balances itself (and all of its subtrees). At any given moment, any given subtree height will differ at most by 1. Maintaining a balanced tree is beneficial because it allows a user to search for a value within it in O(log(n)) time. The main components to implementing a binary search tree are determining balance factors and implementing proper rotations.
A balance factor is simple. Every node has one, and it indicates the difference in height between its two subtrees.
Note that even though this tree appears unbalanced, it is still considered balanced because every balance factor is 1, 0, or -1. As with many tree data structures, certain functions of it can be easily accomplished recursively. Determining a node's balance factor is one such function.
Once we have our balance factors, we use them to determine when a tree needs to be adjusted. Balancing happens as nodes are inserted or deleted, so every time the tree is changed rotations may happen. There are 4 cases for rotations:
- Left Left: a given node has the BF (balance factor) -2 and its left child has BF -1. To balance, rotate clockwise around the node.
- Right Right: a given node has the BF +2 and its right child has BF +1. To balance, rotate counter-clockwise around the node.
- Left Right: a given node has a BF of -2 and its left child BF is +1. To balance, rotate left around child, then right around parent.
- Right Left: a given node has a BF of +2 and its right child BF is -1. To balance, rotate right around child, then left around parent.
While it makes sense to define some simple struct or class to represent each node in the form
class TreeNode {
int data;
TreeNode left;
TreeNode right;
}
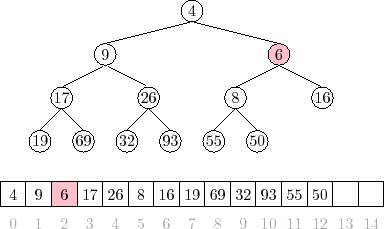
where left and right are references to a node's children, it's worth mentioning that binary trees can be easily represented in arrays as pictured by the following:
any given node at index i has children at indices 2i+1 and 2i+2 (for a 0-indexed array).