查找

[levy9527]

背景

做一个程序：

• 输入：一本英文小说
• 输出：出现次数最多的单词及出现次数

当然小说字数变多时，如何改进数据结构与算法，才能让程序性能令人满意？

分析

这里用到了符号表(symbol table)：ST<word, count>

主要是用到了两个API：

• put
• get

也及涉及到了查找及修改，换句话说，需要一种支持快速查找与修改的数据结构，才能较好地解决问题。

实现

线性结构

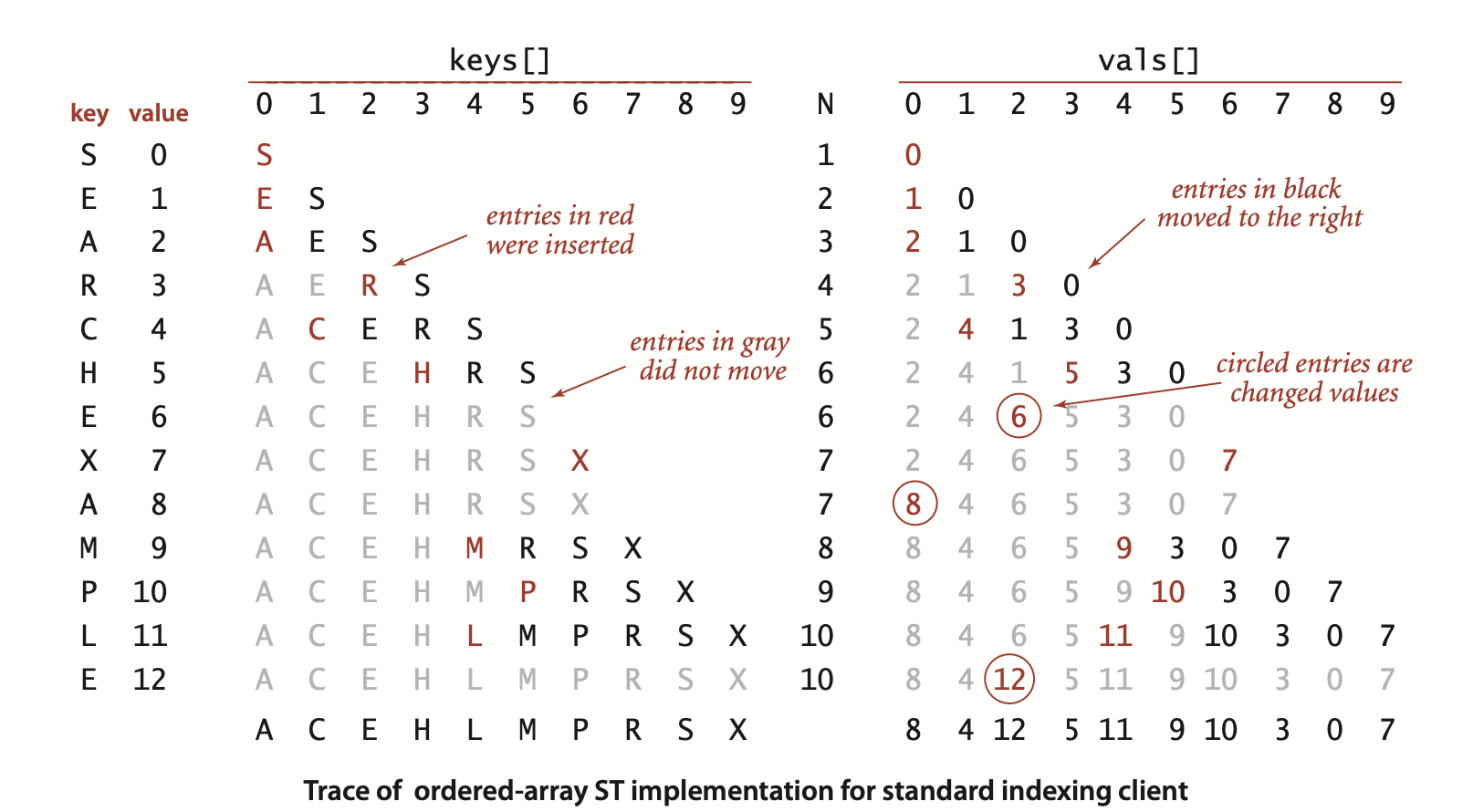
链表可以快速插入（添加一个尾指针），但查找的效率是O（N），不能令人满意。

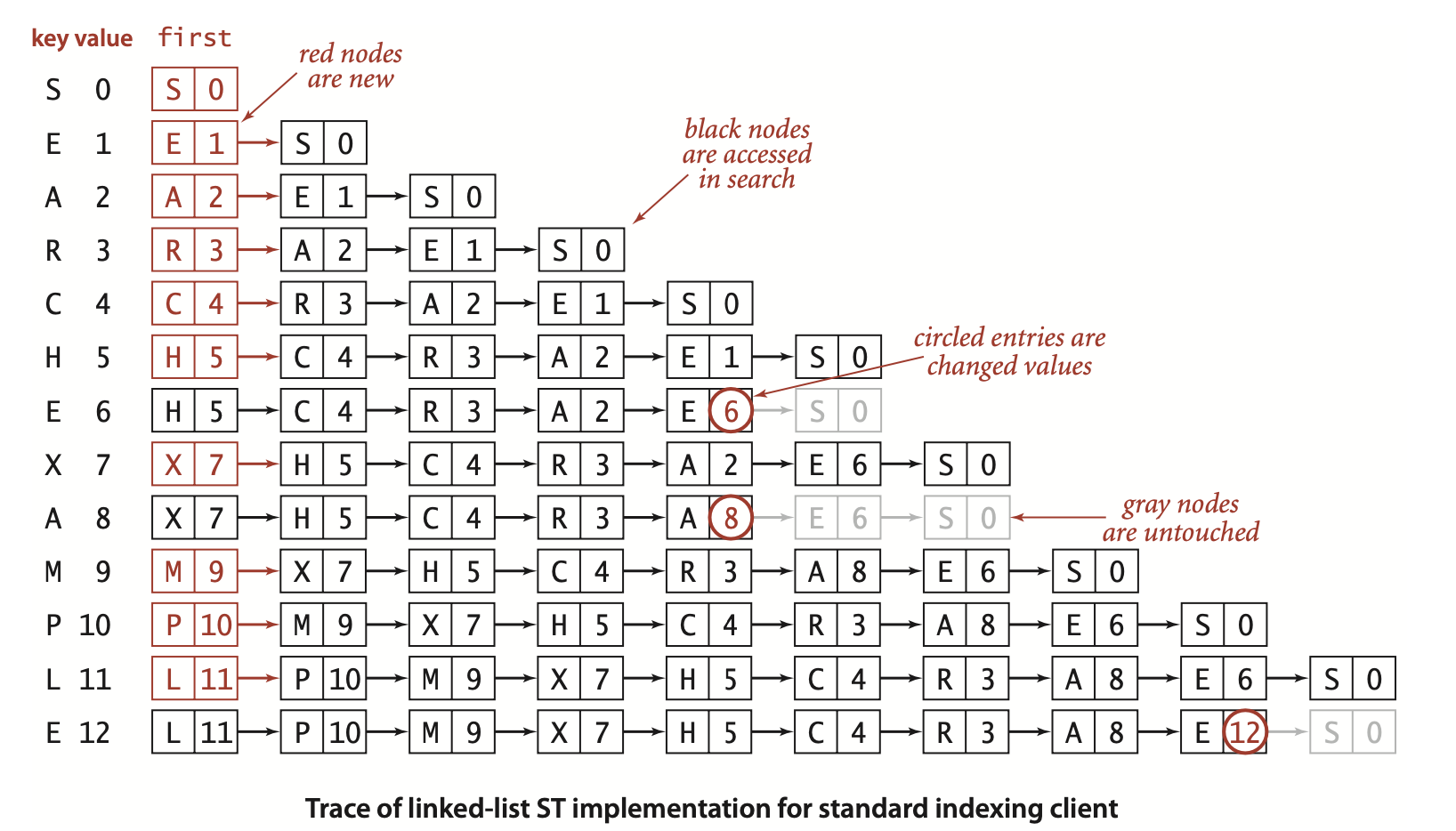
数组（平行数组，一个keys[]，另一个vals[]），有序地插入时，可以利用二分查找，让查找效率为O（lgN）。但其插入效率为O（2N），不能令人满意。

二叉查找树（BST）

BST较好地结合了链表与数组的优点：有序，且支持二分查找，插入与查找的效率都是对数级别。

此外，还较好地支持了：rank、select、delete、range query的操作。

BST的效率取决于树的高度，在极端情况下，会退化成链表，而正是这一潜在的问题，促使进一步的研究。

2-3 树

同时包含2叉节点与3叉节点（中间子节点的值介于父节点两个值之间），自底向上构建，能够自我平衡。

插入后的变化操作如下：（右边的部分省略了对4叉节点的再次分裂操作）

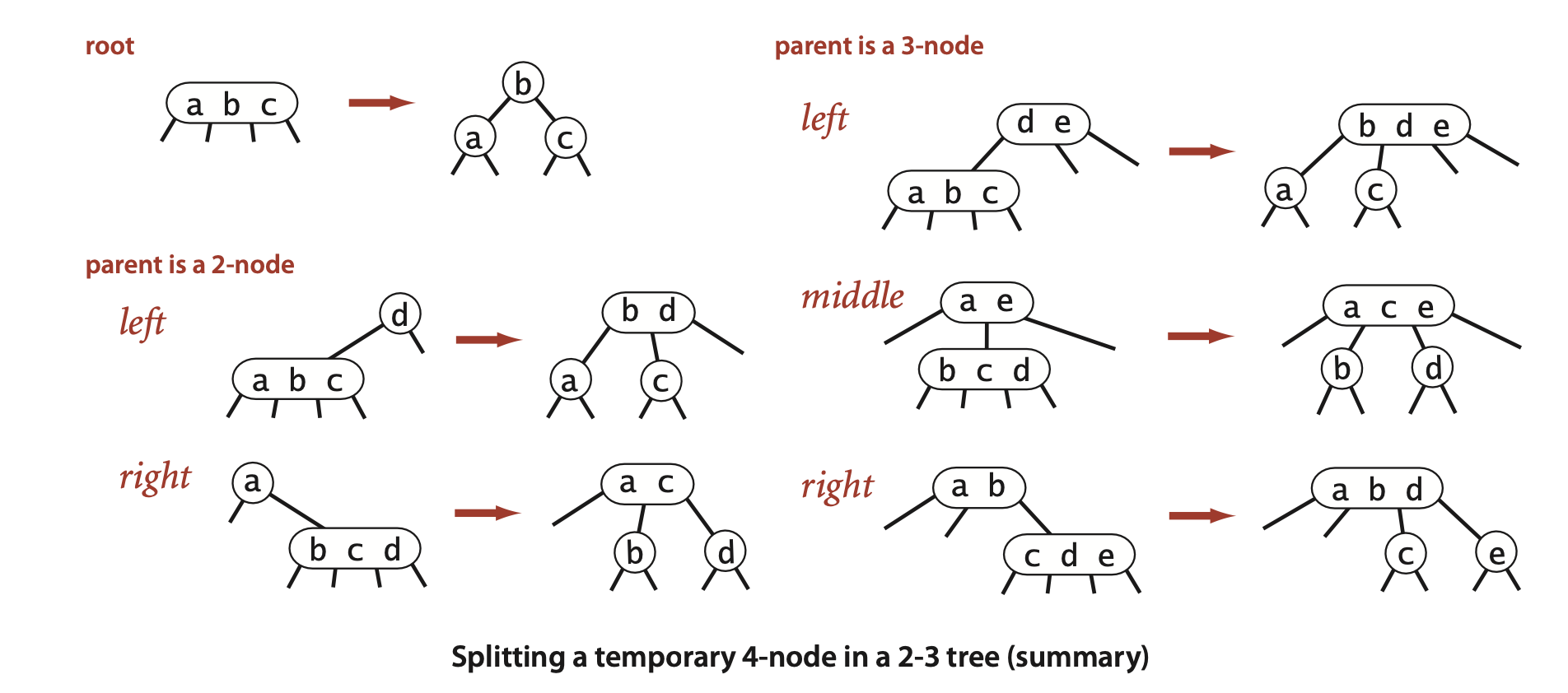
2-3树的难点在于，实现起来比较费力（与红黑树相比），出于工程实践考虑，促使了进一步的研究。

红黑树（Red-Black BST）

基于BST对2-3树的巧妙实现（只需要修改BST的put与delete的代码），如果把红线水平放置，视觉上就更容易看出就是2-3树。

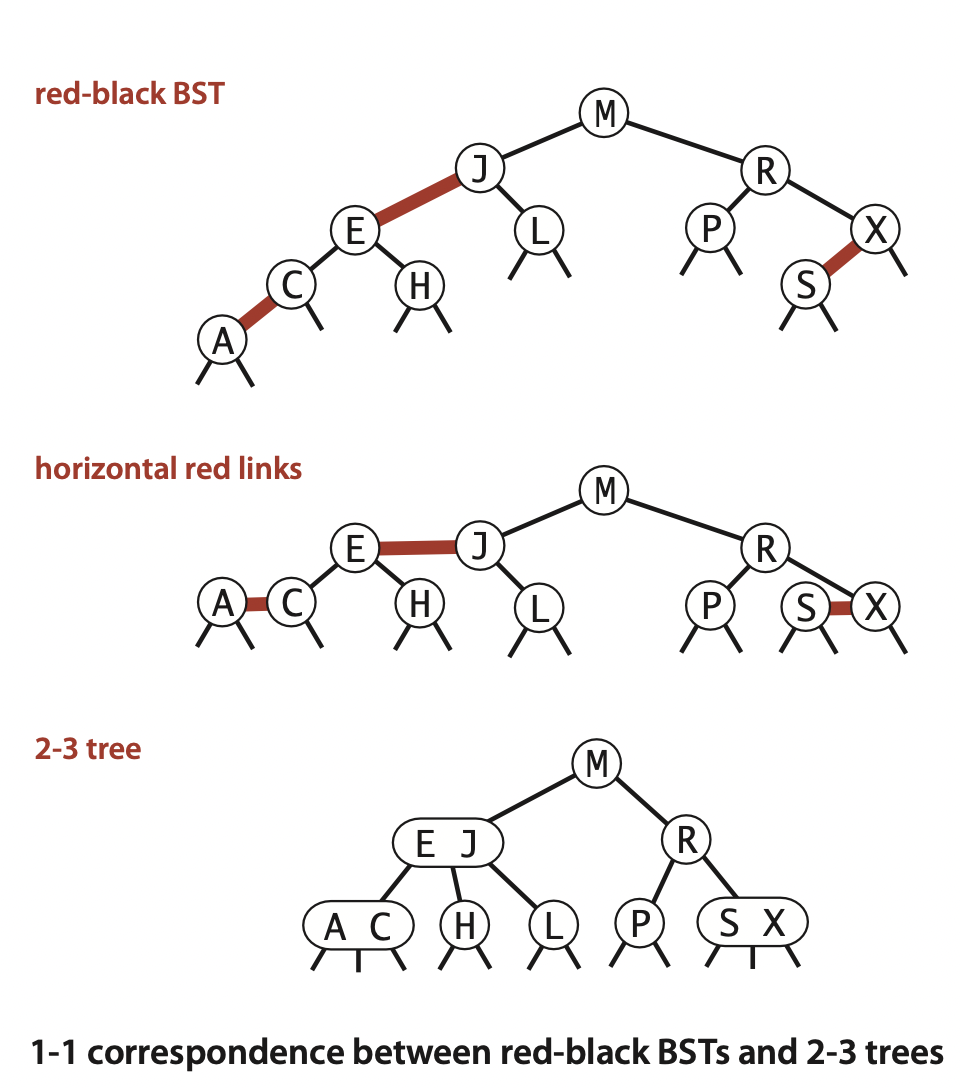
特点有：

1. 根节点一定是黑的
2. 红色要在左孩子节点（这里讨论的是偏左的红黑树）
3. 不能相邻两条边连续红色
4. 是平衡的（每一层左右子树的高度差不超过1）

小测试：答案是3、4（1不平衡，2无序）

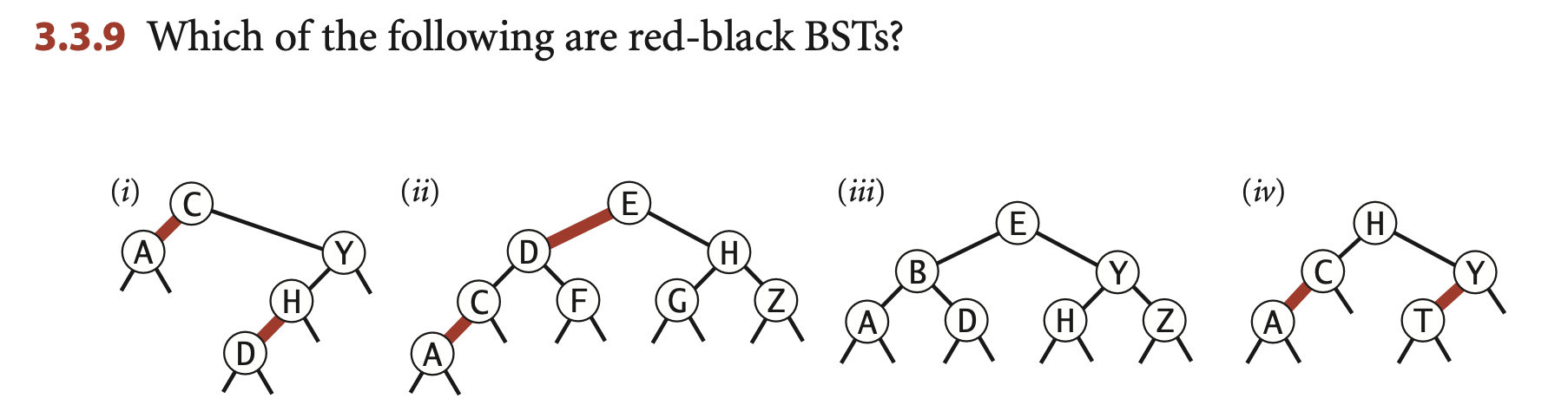
每次插入新节点，都要为新节点染上红色；此时如果违背了上述规则，则需要进行操作

1. 左旋
2. 右旋
3. 反向染色

记录一些细节，可点击查看视频：

1. 递增序列插入，红黑树的高度单调递增（注意与严格单调递增区别开来）
2. 递减序列插入，上述结论不成立

散列表

基于数组可以随机访问的特点，提出设想：如果可以把ST<key, value>的 key 转换成整数，则可以用数组的下标作为 key，从而实现能快速查找与修改的符号表。这样实现的符号表就是散列表。

设散列表数组大小为M，则

核心步骤有两个：

1. 实现散列函数：把 key 转换成整数。关键在于，尽可能均匀（可利用对质数取余计算）
2. 解决散列冲突
   1. separate chaining（数组里装载的是链表）
   2. linear probing（两个平行数组，删除比较棘手，index递增方向挨着的有值的位置，需要重新put）

当然，工程实践上，还要考虑数组的容量扩缩容，以及 load factor 的大小。

linear probing 冲突且走到数组尾总时，会重新在开头查找

练习

1. How many empty lists do you expect to see when you insert N keys into a hash table with SeparateChainingHashST, for N=10, 102, 103, 104, 105, and 106? 思路是利用公式，得出有多少不同的值，则会有多少不同的链表，则总的减去非空的即为答案
2. public int hashCode() { return 17; } 这样的散列函数是合法的（整数）
3. 拉链法使用红黑树
4. bad hash function

public int hashCode()
{
	int hash = 0;
	int skip = Math.max(1, length()/8);
  // this is bad，increase possibility of hash collision
	for (int i = 0; i < length(); i += skip) 
	hash = (hash * 37) + charAt(i);
	return hash;
}

5. 用ST实现Set（dummy value）
6. 如果HashST允许重复key：则put永远新增，不会覆盖
7. 如果RedBlackBST允许重复key：因为旋转的存在，左右子节点都可能是重复的key（BST只会有一边是重复key）
8. 反向对照索引（输入对照索引 concordance——记录每个单词出现的位置，输出原始文本）。我的思路如下：
   1. 位置是关键信息，需要有序。
   2. 则遍历 map<word, pos[]>，拿出所有位置信息，重新 put<pos, word> 进红黑树中
   3. 最后把红黑树中的key由小到大遍历，输出相应的value
   4. 点评：对“索引”的理解不够到位。pos 与字符一一对应，则拿出所有的 pos ，在遍历中设置result[pos] = word 就可以还原原始文本了
9. 不重叠区间的查找。分析如下：
   1. 先对区间进行由小到大排序（因已知不重叠，故比较右边区间即可），记为 partition[]
   2. 遍历 partition[]，判断是否同时满足 partition.min<= input <= partition.right 即可
   3. 为何好像并不涉及ST？
   4. 点评：对“有序时使用二分查找”理解不够深刻。纵然是比较端点，依然可以使用二分查找，所以底层数据结构是红黑树——对有序数据从左至右地扫描，实在是太低效啦。
10. 日程安排。分析如下：
11. 使用ST<teacher，time[]>
12. 判断 time[] 中的某时间段有值时，说明有课，不能再安排课程，否则修改 time[].get(index), put(teacher, time[])
13. LRU缓存。实现步骤如下：
14. 双向链表，有一定容量；
15. 插入前，先查找
    1. 如果未找到，则在头部插入
    2. 如果找到了，则把该节点放到头部
16. 检查是否超出容量
    1. 是，则删除尾部节点
17. 点评：散列表+双向链表 理解不够深刻啊！
    1. 在头部插入，以及尾部删除，这两点理解地没有问题，都是O(1)
    2. 关键是，命中的查找，如何O(1)？如果纯双向链表，是不可能完成这个任务的。所以需要借助散列表来协助查找。
       1. 这里有个陷阱：以为查出 Node 还要用链表再查找一次。其实散列表里存储的是引用，因而可以直接操作节点！
       2. 当然，这就要求，链表直接使用Node来操作，而不是使用集合类如 LinkedList