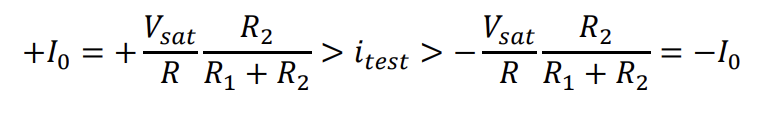diff --git a/2023/10/20/wirteup/index.html b/2023/10/20/wirteup/index.html new file mode 100644 index 0000000..43ab158 --- /dev/null +++ b/2023/10/20/wirteup/index.html @@ -0,0 +1,240 @@ +THUCTF 2023 部分 Writeup | 正在施工中 + + + + + + + + + + + +

THUCTF 2023 部分 Writeup

Created|Updated

THUCTF 2023 Writeup

+

Zirno_81 也许有 copyright

+

一道难题

+

base64 一眼顶针，下一个

+

easymaze

+

用 16 进制读取发现 IEND 数据块后面还有数据，Google 文件尾得知是倒着的 zip 头，于是乎提取出来做倒置得到压缩包（但是得到的压缩包有点损坏直接 WINRAR 修复了）。解压得到一个 linux 可执行文件，先拖进 16 进制读取器里面，得到了 flag1 的明文。
+
+然后才学会用 IDA 逆向，于是乎 shift+F12 找到了奇怪的字符串，结合反编译伪代码猜测是一个迷宫，手动换行得到迷宫图
+
+flag2 is THUCTF{wwdwwdddsssssd}
+

+

麦恩·库拉夫特 - 1

+

实际上可以 /gamemode spectator 然后发现正确路径直接冲就完事了
+

+

关注 THUCTF 谢谢喵

+

关注紫荆园食堂红色圆圈炒宫爆八十一谢谢喵

+

KFC

+

旁边那家店卖 taco，结合一下店名搜到疑似全世界唯一的这家店，于是直接结束
+
+怎么这都要给图啊

+

简单的基本功

+

出题组是不是第一次给的压缩包有问题，我第一次获得的是一个 1kb 不到的压缩包就很呃呃
+出了提示回来看这个题，重新下的压缩包又正常了，于是乎 Google 文件名 + 字节数得到了这个包发布的大概日期，于是乎直接翻官网找到明文文件，然后用 bkcrack 破解提取，得到 flag
+
+以及某位特殊嘉宾
+

+

深奥的基本功

+

读 16 进制发现 pcapng 包在偏移位 5 还是 6 有长达十七八个字节的相同数据。
+继续 bkcrack
+

+

easycrypto

+

你说得对，但是第一问就是纯单表替换而且还知道 THUCTF 和密文的对应关系，于是乎拿到 flag1 和 table，而且 table 大小写之间相同，可以锁定 table 上最后没有确定位置的三个字符
+gettable.py 代码

+
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
if __name__ == '__main__':
    with open("./message.txt","r")as f:
        message = f.readline().strip()

    newtable = ""
    already_get = []
    with open("./cipher.txt","r")as f:
        cipher = f.readline().strip()
        for item in table:
            if (ord(item)>=ord("A")and ord(item)<=ord("Z")) or (ord(item)>=ord("a")and ord(item)<=ord("z")):
                if item in message:
                    index = message.index(item)
                    newtable += cipher[index]
                else:
                    newtable += "{"
                    newtable += item
                    newtable += "}" #用来标记不确定的字符
        newtable += "0123456789+/"
                    

    with open("./table.txt","w")as g:
        g.write(newtable)
+


+读代码发现程序读 table 只读一行，遂推测 table 下面一行是 flag，用已经得到的 table 加换行 THUCTF 跑 ./main 发现与所需内容极其相似。于是乎挨个试验三个字符的所在位置，发现规律疑似单表替换，那么密文就是单表替换后的 base64：VEhVQ1RGe0lfMTB1M182YWMzYjR9，尝试替换后得到 flag
+decoder.py （无法确定最后两个字符所以两种表都试了一遍，最后发现好像没啥影响）

+
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
table1 ="RNPYCLDGBEKQSJZUVMWAITHFXOrnpycldgbekqsjzuvmwaithfxo0123456789+/"
table2 ="RNPYCLDGBEKQSJZUVMWAITFHXOrnpycldgbekqsjzuvmwaitfhxo0123456789+/"
table = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"
if __name__ == '__main__':
    cipher = "TCgTV1MDc0qlSAN1S182XHSoXeM9RR"

    message1 = ""
    message2 = ""
    already_get = []

    for item in cipher:
        if (ord(item)>=ord("A")and ord(item)<=ord("Z")) or (ord(item)>=ord("a")and ord(item)<=ord("z")):
            if item in table1:
                index = table1.index(item)
                message1 += table[index]
        else:
            message1 += item
            
        if (ord(item)>=ord("A")and ord(item)<=ord("Z")) or (ord(item)>=ord("a")and ord(item)<=ord("z")):
            if item in table2:
                index = table2.index(item)
                message2 += table[index]
        else:
            message2 += item

                    
print(message1)
print(message2)
+

测测你的网猫

+

实际上我用的是 socat 捏

+

汉化绿色版免费普通下载

+

拆包
+

+

Z 公司的服务器

+

实际上我是 Google socat 上去的乱码知道的是 rz，不过实际上也可以通过 socat 导出日志来得知是 rz
+
+flag 为 THUCTF{Anc1ent_tr4nsf3r_pr0tOcoI_15_57111_In_u5e_t0d4y}

+

Summary

+

我太菜了，鉴定为到此一游

+
Author: zirno81
Link: http://blog.konpoku.top/2023/10/20/wirteup/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/05/23/EEDA/index.html b/2024/05/23/EEDA/index.html new file mode 100644 index 0000000..44507d7 --- /dev/null +++ b/2024/05/23/EEDA/index.html @@ -0,0 +1,260 @@ +清华电子系数算 OJ 通关指北 | 正在施工中 + + + + + + + + + + + +

清华电子系数算 OJ 通关指北

Created|Updated

写在基石前面

+

下面这段话来自于 NJU 计算机系统概论 PA 文档，值得一读。

+
+

基础设施 - 提高项目开发的效率
+在PA中, 基础设施是指支撑项目开发的各种工具和手段. 原则上基础设施并不属于课本知识的范畴, 但是作为一个有一定规模的项目, 基础设施的好坏会影响到项目的推进, 甚至决定项目的成败, 这是你在程序设计课上体会不到的.

+

事实上, 你已经体会过基础设施给你带来的便利了. 我们的框架代码已经提供了Makefile来对NEMU进行一键编译. 假设我们并没有提供一键编译的功能, 你需要通过手动键入gcc命令的方式来编译源文件: 假设你手动输入一条gcc命令需要10秒的时间(你还需要输入很多编译选项, 能用10秒输入完已经是非常快的了), 而NEMU工程下有30个源文件, 为了编译出NEMU的可执行文件, 你需要花费多少时间? 然而你还需要在开发NEMU的过程中不断进行编译, 假设你需要编译500次NEMU才能完成PA, 一学期下来, 你仅仅花在键入编译命令上的时间有多少?

+

有的项目即使使用工具也需要花费较多时间来构建. 例如硬件开发平台vivado/quartus一般需要花费半小时到一小时不等的时间来生成比特文件, 也就是说, 你编写完代码之后, 可能需要等待一小时之后才能验证你的代码是否正确. 这是因为, 这个过程不像编译程序这么简单, 其中需要处理很多算法上的NPC问题. 为了生成一个质量还不错的比特文件, 硬件开发工具需要付出比gcc更大的代价来解决这些NPC问题. 这时候基础设施的作用就更加重要了, 如果能有工具可以帮助你一次进行多个方面的验证, 就会帮助你节省下来无数个"一小时".

+

Google内部的开发团队非常重视基础设施的建设, 他们把可以让一个项目得益的工具称为Adder, 把可以让多个项目得益的工具称为Multiplier. 顾名思义, 这些工具可以成倍提高项目开发的效率. 在学术界, 不少科研工作的目标也是提高开发效率, 例如bug自动检测和修复, 自动化验证, 易于开发的编程模型等等. 在PA中, 基础设施也会体现在不同的方面, 我们会在将来对其它方面进行讨论.

+

你将来肯定会参与比PA更大的项目, 如何提高项目开发的效率也是一个很重要的问题. 希望在完成PA的过程中, 你能够对基础设施有新的认识: 有代码的地方, 就有基础设施. 随着知识的积累, 将来的你或许也会投入到这些未知的领域当中, 为全世界的开发者作出自己的贡献.

+
+

面对数算OJ如同黑盒一般的测试，“基础设施”的重要性更是不言而喻。为了高效的解决挑战OJ时所遇到的各种问题，你可能还需要补充下面的一些知识
+本人不保证下述内容的可靠性，欢迎纠错和与笔者讨论

+

基石

+

调试

+

善用工具
+机器的效率和准确度往往比人高，比起瞪眼盯着自己写的代码半天看不出来个所以然，不如交给机器分步运行程序，自己则坐在一旁观察程序运行状态的变化来 Debug。
+使用现代调试工具几乎是你想要通过OJ所必须要掌握的技能。程设课上所使用的 Visual Studio 自带调试工具。而笔者一般使用 vscode 插件，配合 gdb 进行调试。
+另外，如果你会使用 g++ 或者 clang++ 之类的编译器进行手动编译，或者改 vscode 的配置文件来添加编译选项，那么笔者强烈推荐在编译选项中加入 -fsanitize=address 和 -g，这样如果程序出现了数组越界，访问空指针等非法操作，程序会能够中断并且反馈信息（会反馈的时候出现问题时程序执行到的位置），这有利于解决 RE 相关的错误
+使用assert
+在程序中使用 assert 宏来对程序的运行状况作出限定，能够更早的将问题暴露出来（譬如在访问 a[n] 前用 assert 检测 n 是否超出了数组范围，或者进行空指针检查，这样能比较好的追踪非法访问内存所产生的问题）

+

随机样例生成和 DiffTest

+

学会写python
+python 是一种非常易用易学的编程语言，在这里你不用总是关心数组越界，int 溢出等问题，也不用被 c 和 c++ 里面一些不易用的东西困扰。用这样的一门语言写一些临时的小工具是相当好用的（比如后文将会提到的随机样例生成器）。
+自己造样例
+OJ 平台上所用的测试数据是不公开的，而自己手造样例仅仅在数据范围很小的时候可行（而且经常很烦人）。为了使用量大且复杂的数据对代码在本地进行测试（同时使用测试工具追踪 WA 或者 RE），自己手捏一个随机样例生成器相当重要。你还可以将生成器进行调教调整以生成不同特征的样例，进行针对性的测试

+

DiffTest
+DiffTest，中文叫差分测试，俗称对拍，说白了就是找个“能保证结果是对的”程序，和我们自己写的程序的输出做对比，以此来发现问题所在。这样的程序对性能没有多高的要求，往往可以使用暴力方法求解答案。程序可以和随机样例测试结合起来，因为手算随机大样例的结果往往是不可行的。此外，有的时候程序仅在少数情况下结果出错，就更需要我们进行输出结果的对比，获得使得程序出错的样例，再使用调试工具进行进一步的检查。

+

发挥C++本身的潜力

+

C++ 提供了很多好用的数据结构和函数的模板，你可以在许多成熟的代码中发现他们的影子。
+标准模板库帮你解决了很多问题，比如数组的排序可以使用 algorithm 头文件中的 std::sort() 函数来解决。
+当然 STL 的用法太多了，有的时候也不一定适用于题目（可能带来额外的开销，比如电子系最喜欢的#include<iostream>爆内存），需要具体问题具体分析
+除了 STL，C++的许多现代特性也能够加速你的开发进度，譬如自动类型推断和简化的for循环语法

+
1
2
3
4
5
std::vector<int> vec = (5,0);
for (auto num : vec)
{
    // Iterate through the vector
}
+

或者是 lambda function

+
1
2
3
std::sort(vec.begin(),vec.end(),[](int a,int b) -> int {
    return a > b;
});
+

增加代码的可读性

+

别随便命名
+总有人喜欢用 abcd 或者中文拼音对变量或者函数命名，但是这种不能一眼看懂的命名往往会导致致命性的效率下降（用不了两分钟你就忘了之前写的变量 e 是什么意思了）
+在这里笔者推荐两种常见的命名方法：

+
驼峰命名法
+

对于函数，类等的命名，每个单词首字母大写
+譬如 GetVal, PriorityQueue
+对于变量的命名，第一个单词首字母小写，后面的单词首字母大写
+譬如 playerBlood，matrixIndex

+
下划线命名法
+

每个单词中间用下划线分割开来
+比如 player_blood，get_val

+

善用宏和函数
+假如你要求两个数的最大值，你第一时间想到的可能是

+
1
int max_num = a < b ? b : a;
+

那假如你要重复使用最大值的功能呢？

+
1
2
3
4
5
6
int max_num = a < b ? b : a;
max_num = c < h ? h : c;
max_num = d < i ? i : d;
max_num = e < j ? j : e;
max_num = f < k ? k : f;
max_num = g < l ? l : g;
+

你可能已经发现了，如果你要重复多次求不同的数对的最大值，写这样的一条表达式是一件非常痛苦的事情，而且这样的代码可读性很差
+此时可以使用函数

+
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int max(int a,int b)
{
    return a < b ? b : a;
}

int main()
{
    max_num = max(a,b);
    max_num = max(c,h);
    max_num = max(d,i);
    max_num = max(e,j);
    max_num = max(f,k);
    max_num = max(g,l);
}
+

这样写起来简单易读（当然更直接的是使用std::max）
+对于求最大值这样比较简单的操作也可以使用宏替换
+（使用宏的时候需要全大写，使用下划线分割单词）
+（一定要注意使用宏的规范性，避免遇到一些难以调试的问题）

+
1
2
3
4
5
6
7
8
9
10
#define MAX(a,b) ((a) < (b) ? (b) : (a))
int main()
{
    max_num = MAX(a,b);
    max_num = MAX(c,h);
    max_num = MAX(d,i);
    max_num = MAX(e,j);
    max_num = MAX(f,k);
    max_num = MAX(g,l);
}
+

max别用宏定义！这里只是举例！
+常用的常数也可以使用宏替换
+嫌 long long 之类的太长了也可以用宏替换或者 typedef

+
1
2
3
4
5
6
#define VEC_SIZE 81*114514
#define uint32 unsigned int
typedef long long int64;
vector<int> stu_id(VEC_SIZE);
vector<uint32> stu_score(VEC_SIZE);
int64 stu_num;
+

开拓眼界

+

为了解决OJ中的难题，你可能需要使用各种阴间技巧或者课上没有教的算法。这些算法你可能可以在OI WIKI中找到。
+尽量使用高效的搜索引擎（百度实在是太垃圾了）
+具体代码方面的问题可以在 runoob 和 stackoverflow 等网站中搜索答案

+

最后再次提醒大家，人生很精彩，适度娱乐，拒绝内卷。祝各位OJ愉快！

+
Author: zirno81
Link: http://blog.konpoku.top/2024/05/23/EEDA/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/11/15/EEEC1-1/index.html b/2024/11/15/EEEC1-1/index.html new file mode 100644 index 0000000..759cf3d --- /dev/null +++ b/2024/11/15/EEEC1-1/index.html @@ -0,0 +1,300 @@ +电子电路与系统基础复习（1）二端口网络参量：一切故事的开始 | 正在施工中 + + + + + + + + + + + +

电子电路与系统基础复习（1）二端口网络参量：一切故事的开始

Created|Updated

网络参量的引入

+

对于一个电路系统来说，最朴素的认知是认为系统分别有输入输出两个端口，因此对二端口网络的描述是最为重要并且基础的。
+我们所能直接测量的无非网络的电流和电压，两个端口也就是两组电流和电压，对于线性网络来说，我们很容易能够列出来四个变量组成的二元一次方程组
+比如对如图所示的二端口网络，我们可以列出如下的方程组
+alt text

+

v1=(R1+R2)i1+R2i2v2=R2i1+R2i2v_1 = (R_1+R_2)i_1 + R_2i_2 \\\\ +v_2 = R_2i_1 + R_2i_2 +

+

矩阵形式也就是

+

[v1v2]=[R1+R2R2R2R2][i1i2]\begin{gathered} +\begin{bmatrix} v_1 \\\\ v_2 \end{bmatrix} = +\begin{bmatrix} R_1+R_2 & R_2 \\\\ R_2 & R_2 \end{bmatrix} +\begin{bmatrix} i_1 \\\\ i_2 \end{bmatrix} +\end{gathered} +

+

那么不妨就将上面的矩阵作为网络的的一个描述，以此我们得到了二端口网络的z参量描述

+

[v1v2]=[z11z12z21z22][i1i2]\begin{gathered} +\begin{bmatrix} v_1 \\\\ v_2 \end{bmatrix} = +\begin{bmatrix} z_{11} & z_{12} \\\\ z_{21} & z_{22} \end{bmatrix} +\begin{bmatrix} i_1 \\\\ i_2 \end{bmatrix} +\end{gathered} +

+

类似的我们还有其他种类的参量

+

[i1i2]=[y11y12y21y22][v1v2]\begin{gathered} +\begin{bmatrix} i_1 \\\\ i_2 \end{bmatrix} = +\begin{bmatrix} y_{11} & y_{12} \\\\ y_{21} & y_{22} \end{bmatrix} +\begin{bmatrix} v_1 \\\\ v_2 \end{bmatrix} +\end{gathered} +

+

[v1i2]=[h11h12h21h22][i1v2]  [i1v2]=[g11g12g21g22][v1i2]\begin{gathered} +\begin{bmatrix} v_1 \\\\ i_2 \end{bmatrix} = +\begin{bmatrix} h_{11} & h_{12} \\\\ h_{21} & h_{22} \end{bmatrix} +\begin{bmatrix} i_1 \\\\ v_2 \end{bmatrix} +\end{gathered} +\space \space +\begin{gathered} +\begin{bmatrix} i_1 \\\\ v_2 \end{bmatrix} = +\begin{bmatrix} g_{11} & g_{12} \\\\ g_{21} & g_{22} \end{bmatrix} +\begin{bmatrix} v_1 \\\\ i_2 \end{bmatrix} +\end{gathered} +

+

[v1i1]=[ABCD][v2i2]  [v2i2]=[abcd][v1i1]\begin{gathered} +\begin{bmatrix} v_1 \\\\ i_1 \end{bmatrix} = +\begin{bmatrix} A & B \\\\ C & D \end{bmatrix} +\begin{bmatrix} v_2 \\\\ i_2 \end{bmatrix} +\end{gathered} +\space \space +\begin{gathered} +\begin{bmatrix} v_2 \\\\ i_2 \end{bmatrix} = +\begin{bmatrix} a & b \\\\ c & d \end{bmatrix} +\begin{bmatrix} v_1 \\\\ i_1 \end{bmatrix} +\end{gathered} +

+

上面的参量依次被称为阻抗参量，导纳参量，混合参量，混合参量，传递参量，逆传参量。
+他们具有以下的等效电路
+alt text
+其中每个矩阵中下标为21的项都可以视作从输入到输出的增益，如上图所示。
+对于参量的求取有下面的规则
+alt text
+传输参量要特殊一些，ABCD四个参量的倒数为端口1到端口2的四个本征增益（传输矩阵直接表示从输入端口到输出端口的关系，所以是“本征”）
+下面是我最喜欢的一张图，当初课上引起一番轰动
+alt text
+这里是比较重要的计算规则
+alt text
+级联的话则是ABCD矩阵相乘（简单的线性代数知识）
+现在我们对网络参量有了一个基本的概念，下面要通过网络参量的方法来分析电路系统的性质。
+TODO:第五讲PPT,回路电流与节点电压法

+
Author: zirno81
Link: http://blog.konpoku.top/2024/11/15/EEEC1-1/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/11/18/EEEC2-2/index.html b/2024/11/18/EEEC2-2/index.html new file mode 100644 index 0000000..22afaf6 --- /dev/null +++ b/2024/11/18/EEEC2-2/index.html @@ -0,0 +1,349 @@ +电子电路与系统基础（2）：（二）大信号放大器 | 正在施工中 + + + + + + + + + + + +

电子电路与系统基础（2）：（二）大信号放大器

Created|Updated

高增益放大器

+

最初步的肯定是我们之前学过的小信号放大器。

+

image-20241123112317947

+

将晶体管反相器偏置在工作电压处，提供极大的交流电阻，以获得高电压增益。能够实现Av0=−gm(rds1∥rds2)A_{v_0}= -g_m(r_{ds1}\parallel r_{ds2})的放大增益。

+

image-20241123113105966

+

但是问题是，如果加一个小电阻负载，需要我们提供大电流，也就是在等效模型的输出端并联一个小电阻，那么很容易看到输出端总电阻减小到RLR_L数量级，输出电压也急剧减小

+

为了解决这个问题，我们在输出端添加电压缓冲器来提供大电流。电压缓冲器具有输出高电流的能力

+

image-20241123131459676

+

image-20241123131712618

+

大信号放大器

+

A类放大器

+

image-20241123132329135

+

其中VBV_B为直流偏置电压，用来固定流过Q2的电流大小。然后输入VIV_I来控制流过Q1的电流，Q2和Q1之间流过电流有差值，即等于RLR_L流过的电流，产生VOV_{O}

+

A类放大器的主要问题在于他的效率很低，这主要是因为整个周期内平均下来Q2提供的电流总是有一部分要流过Q1，而不是全部加到负载上，这造成了75%75\%的的功率损耗

+

由于电路是交流，可以用大电感来代替Q2电阻，大电感不实际消耗功率，那么A类放大器的理论效率也只能到达50%50\%

+

AB类放大器

+

image-20241123133340548

+

这里的重点是直流偏置VBV_B很小，使得两个晶体管微微导通。Q1处于CC组态，是电压跟随器，在输入信号的正半周的时候，Q1发射极的电压跟随基极发生变化，VO=VI+VB−0.7V<VI+0.7VV_O = V_I + V_B - 0.7V < V_I+0.7V，可以看到Q2处于近乎截止状态，基本上不怎么吸收电流，大部分电流都被负载吸收

+

负半周的时候，就反过来了，此时Q2发射极的电压跟随基极发生变化，VO=VI+0.7V>VI+VB−0.7VV_O = V_I + 0.7V > V_I + V_B - 0.7V，可以看到Q1处于近乎截止状态，基本上不怎么吸收电流，Q2提供的电流基本上都被负载吸收

+

这种结构叫推挽结构，两个晶体管分别在输出正弦波的正负周期为负载提供电流

+

B类放大优化到AB类放大

+

我操。glgg为什么不先告诉我们什么是A类放大什么是B类放大，有病吧。。

+

A类放大我们前面讲过了，现在来讲B类放大

+

image-20241123135932987

+

可以看到这里少了偏置，没有静态功耗，但是这会导致很多问题。首先是CC组态的电压跟随有0.7V的损耗，其次是当输入电压小于正负0.7V的时候，Q1和Q2都没有导通，导致这附近的输出有严重失真。

+

image-20241123141947596

+

效率理论值为78%78\%

+

因此我们使用AB类放大，我们认为IPUSH.IPULL=ConstantI_{PUSH} . I_{PULL} = Constant

+

由于直流偏置的存在推拉二管在0.7V附近的时候能够更好的导通，从而减小输出的失真

+

下面进行效率的计算

+

image-20241123150937701

+

这里预设推挽结构的最大工作电流是13mA13mA，换句话说就是最大输出电压是13V13V

+

没有交流输入时候的静态功耗为PDC=(VCC+VEE)IQ=4.65mWP_{DC} = (V_{CC} + V_{EE})I_Q = 4.65mW，输入为正弦波的时候，负载上的功率为

+

PL=12vop2RL=121321k=84.5mWP_L = \frac{1}{2}\frac{v_{op}^2}{R_L} = \frac{1}{2}\frac{13^2}{1k} = 84.5mW +

+

而电路所消耗的总功率为

+

PCC−EE=12π∫02πIC2VCCdωt+12π∫02πIC1VEEdωt≈1π∫0π13sin⁡ωtdωt−12π∫π2π13sin⁡ωtdωt=124mWη=68%\begin{align*} +P_{CC-EE} &= \frac{1}{2\pi}\int^{2\pi}_{0}I_{C2}V_{CC}d \omega t + \frac{1}{2\pi}\int^{2\pi}_{0}I_{C1}V_{EE}d \omega t\\ +&\approx \frac{1}{\pi}\int^{\pi}_{0}13 \sin \omega td \omega t - \frac{1}{2\pi}\int^{2\pi}_{\pi}13 \sin \omega td \omega t = 124mW\\ +\eta &= 68 \% +\end{align*} +

+

差分对

+

反正差分对就是长这么一个样子的东西

+

image-20241123152402925

+

能够看到差分对只放大Vip−VinV_{ip} - V_{in}，也就是差模信号。使用差分放大的一个好处是能够过滤掉公共地上的噪声信号。

+

image-20241123155257856

+

差分信号可以等效为一个差模地和两个差模电压源

+

差分对的共模输入范围

+

主要是要确保晶体管工作在恒流区。这里的晶体管包括提供直流偏置电流的晶体管。

+

image-20241123160814100

+

这里假设没有差模输入。对于M1和M2，两边各分得一半电流

+

0.5ISS=βnVod02⇒Vod0=ISS2βn0.5I_{SS} = \beta_n V_{od0}^2 \Rarr V_{od0} = \sqrt{\frac{I_{SS}}{2\beta_n}} +

+

两个MOS管的漏极就有

+

VD=VD1=VD2=VDD−0.5ISSRDV_{D} = V_{D1} = V_{D2} = V_{DD} - 0.5 I_{SS}R_D +

+

M1和M2处于恒流区的条件为

+

vic=vG<vD+vTH=VDD−0.5ISSRD+VTH=VI,CM,maxv_{ic} = v_G < v_D + v_{TH} = V_{DD} - 0.5I_{SS}R_D + V_{TH} = V_{I,CM,max} +

+

偏置晶体管处于恒流区的条件为(这里vsv_s即为偏置晶体管的漏极电压)

+

vS>Vsatvic=vG=vS+VGS>Vsat+VTH+Vod0=VI,CM,minv_S > V_{sat}\\ +v_{ic} = v_G = v_S + V_{GS} > V_{sat} + V_{TH} + V_{od0} = V_{I,CM,min} +

+

得到了全部条件

+

差分对的差模输入范围

+

主要是保证两个差分对管能够工作在恒流区，这里不需要担心直流偏置的问题，因为至少有一侧的vicv_{ic}是大于vI,CM,minv_{I,CM,min}的。

+

image-20241123162808250

+

有差模电压，两条支路上就有差模电流（如图所示），差模电流的大小是受限的，因为0.5ISS−0.5iD>00.5I_{SS} - 0.5i_D > 0，不然MOS管就截止了

+

直接考虑临界状态，id=ISSi_d = I_{SS}，容易得到Vod1=ISSβn,Vod2=0V_{od1} = \sqrt{\frac{I_{SS}}{\beta_n}},V_{od2} = 0

+

Vid,max=vGS1−vGS2=Vod1−Vod2=2Vod0V_{id,max} = v_{GS1} - v_{GS2} = V_{od1} - V_{od2} = \sqrt{2}V_{od0} +

+

得出了结论

+

大信号输入输出转移特性

+

vo=idRDv_o = i_d R_D，所以这里主要研究idi_d

+

容易看到的是

+

VGS1=ISS+id2βn+VTH,VGS2=ISS−id2βn+VTHVGS1−VGS2=vid,ISS=2βnVod02V_{GS1} = \sqrt{\frac{I_{SS}+i_d}{2\beta_n}} + V_{TH}, V_{GS2} = \sqrt{\frac{I_{SS}-i_d}{2\beta_n}}+V_{TH}\\ +V_{GS1} - V_{GS2} = v_{id}, I_{SS} = 2\beta_n V_{od0}^2 +

+

反正经过一番计算就能够得到

+

id=βnvid4Vod02−vid2=ISSvidVod01−14(vidvod0)2i_d = \beta_n v_{id}\sqrt{4 V_{od0}^2 - v_{id}^2} = I_SS \frac{v_{id}}{V_{od0}}\sqrt{1-\frac{1}{4}(\frac{v_{id}}{v_{od0}})^2} +

+

image-20241123164451810

+

小信号分析

+

我操，glgg真tm能讲

+

image-20241123165000343

+

去掉直流偏置，第一次等效

+

image-20241123165034431

+

第二次等效

+

vodif=0.5gm0vid(2rds∥2RD)=gm0vid(rds∥RD)A=gm0(rds∥RD)v_{odif} = 0.5g_{m0} v_{id} (2r_{ds}\parallel 2R_D) = g_{m0} v_{id} (r_{ds}\parallel R_D) \\ +A = g_{m0}(r_{ds}\parallel R_D) +

+

反正就是理想晶体管那一套东西，没记下来，等以后更新吧

+

双端转单端

+

image-20241123165707052

+

反正就是上面是一个电流镜，然后Q1和Q2分走的电流大小不一样，所以多出来的电流流出来形成增益。另外一种情况是求本征电压增益（此时vov_o端开路，此时电流是以厄利电流的形式被消解掉的，所以增益里面写的是gm0(rce2∥rce4)g_{m0}(r_{ce2}\parallel r_{ce4})，其中rce2r_{ce2}和rce4r_{ce4}是两个晶体管厄利效应的等效

+

image-20241123170048704

+

Q3被等效为电阻主要是因为基极和集电极相连，所以输出电流和电压成正比，等效为电阻

+
Author: zirno81
Link: http://blog.konpoku.top/2024/11/18/EEEC2-2/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/11/18/PDE1/index.html b/2024/11/18/PDE1/index.html new file mode 100644 index 0000000..c2bde17 --- /dev/null +++ b/2024/11/18/PDE1/index.html @@ -0,0 +1,389 @@ +数理方程学习笔记（一）：波动方程初步 | 正在施工中 + + + + + + + + + + + +

数理方程学习笔记（一）：波动方程初步

Created|Updated

特征线法

+

常系数运输方程初值问题

+

对于方程

+

∂tρ+a∂xρ=0,x∈R,t>0\partial_t \rho + a \partial_x \rho = 0, x \in \mathbb{R}, t > 0 +

+

给定初值条件

+

ρ(x,0)=ρ0(x)\rho(x,0) = \rho_0(x) +

+

我们发现在特征线上，ρ\rho 保持不变，然后通过特征线反推每一点ρ\rho的值
+具体而言是这样的，特征线是下面的常微分方程初值问题的解

+

dxdt=a,x(0)=x0\frac{\rm{d}x}{\rm{d}t} = a, x(0) = x_0 +

+

其实这条线就是x(t,x0)=at+x0x(t,x_0) = at + x_0，但是写成微分形式其实是为了下面的推导
+根据全微分公式

+

df=∂f∂xdx+∂f∂tdt\rm{d}f = \frac{\partial f}{\partial x} \rm{d}x + \frac{\partial f}{\partial t} \rm{d}t +

+

我们有

+

dρ=∂xρdx+∂tρdt\rm{d}\rho = \partial_x \rho \rm{d}x + \partial_t \rho \rm{d}t +

+

dρdt=∂xρdxdt+∂tρ=∂tρ+a∂xρ=0\frac{\rm{d}\rho}{\rm{d}t} = \partial_x\rho \frac{\rm{d}x}{\rm{d}t} + \partial_t \rho = \partial_t \rho + a\partial_x \rho = 0 +

+

最后一步推导使用了原方程条件
+上面的推导表明在特征线上ρ\rho为常数，因此对于(x,t)(x,t)平面上的任何一个点(x0,t0)(x_0,t_0)，我们都可以找到一条过该点的的特征线x(t,x0−at0)=a(t−t0)+x0x(t,x_0 - at_0) = a(t-t_0) + x_0，这条线与t=0t=0有一交点x=x0−at0x=x_0-at_0，在该点ρ\rho的值是确定的（初值条件），有ρ(x0−at0,0)=ρ0(x0−at0)\rho(x_0-at_0,0) = \rho_0(x_0-at_0)
+实际上我们就推导出了ρ(x,t)=ρ0(x−at)\rho(x,t) = \rho_0(x-at)

+

值得注意的事情是，我们不妨画出t=0t=0的时候ρ\rho随xx变化的图像，那么tt变大即图像右移，tt减小即图像左移，因此被称为输运方程

+

变系数输运方程初值问题

+

现在来讨论更为复杂的情况

+

∂tρ+∂x(v(x)ρ)=0,ρ(x,0)=ρ0(x),x∈R,t>0\partial_t \rho + \partial_x(v(x)\rho) = 0, \rho(x,0) = \rho_0(x), x\in \mathbb{R}, t > 0 +

+

经过数学家不知道多少年的研究我们知道这个方程的特征线长这样

+

dxdt=v(x(t)),x(0)=x0\frac{\rm{d}x}{\rm{d}t} = v(x(t)), x(0) = x_0 +

+

然后我们把方程稍微变形一下，把变系数拿出来

+

∂tρ+v(x)∂xρ=−v′(x)ρ\partial_t \rho + v(x)\partial_x \rho = -v'(x)\rho +

+

同样对ρ\rho求全微分

+

dρdt=∂tρ+dxdt∂xρ=∂tρ+v(x)∂xρ=−v′(x)ρ\frac{\rm{d}\rho}{\rm{d}t} = \partial_t \rho + \frac{\rm{d}x}{\rm{d}t}\partial_x \rho =\partial_t \rho + v(x)\partial_x\rho= -v'(x)\rho +

+

比起其他妖魔鬼怪，这个方程实在是太好解了！
+将方程改写成我们熟悉的形式

+

dρρ=−v′(x)dt\frac{\rm{d}\rho}{\rho} = -v'(x)\rm{d}t +

+

两边积分

+

ln⁡ρ(x(t,x0),t)−ln⁡ρ0(x0)=−∫0tv′(x)dτ\ln \rho(x(t,x_0),t) - \ln \rho_0(x_0) = -\int^t_0 v'(x) \rm{d}\tau +

+

这里有几点需要注意的，首先是我们代入了ρ(x,0)=ρ0(x)\rho(x,0)=\rho_0(x)的初值条件
+其次稍微换了一下符号，因为这里我们是对[0,t][0,t]区间积分，把原来的tt换成了τ\tau
+继续变换（使用了dx/dτ=v(x(τ))\rm dx/d\tau = v(x(\tau))）

+

−RHS=∫0tv′(x(τ))dτ=∫0tv′(x(τ))v(x(τ))dxdτdτ=∫x0x(t,x0)v′(x)v(x)dx=ln⁡v(x(t,x0))v(x0)-RHS = \int^t_0 v'(x(\tau))\rm{d}\tau = \int^t_0 \frac{v'(x(\tau))}{v(x(\tau))}\frac{\rm{d}x}{\rm{d}\tau} \rm{d}\tau = \int^{x(t,x_0)}_{x_0} \frac{v'(x)}{v(x)}\rm{d}x = \ln \frac{v(x(t,x_0))}{v(x_0)} +

+

整理一下就是

+

ρ(x(t,x0),t)=ρ0(x0)v(x0)v(x(t,x0))\rho(x(t,x_0),t) = \rho_0(x_0)\frac{v(x_0)}{v(x(t,x_0))} +

+

接下来还有一点问题，其实刚刚的x0x_0是任意的，现在我们需要根据确定的tt来反推x0x_0。这个事情通过求解特征线方程来解决，我们先求dx/dt=v(x(t)),x(0)=x0\rm dx/dt = v(x(t)),x(0)=x_0的解为x=x(t,x0)x=x(t,x_0)，然后反推就能得到x0=φ(x,t)x_0=\varphi(x,t)
+最终的结果是

+

ρ(x,t)=ρ0(φ(x,t))v(φ(x,t))v(x)\rho(x,t) = \rho_0(\varphi(x,t))\frac{v(\varphi(x,t))}{v(x)} +

+

不管你晕没晕，反正笔者是晕了这里给出一个例题帮助理解

+

例题1

+

求下面初值问题的解

+

∂tu+(x+t)∂xu+u=0,u(x,0)=x,x∈R,t>0\partial_t u + (x+t)\partial_x u + u = 0, u(x,0) = x, x\in \mathbb{R}, t > 0 +

+

特征线是

+

dxdt=x+t,x(0)=x0\frac{\rm dx}{\rm dt} = x+t, x(0) = x_0 +

+

代入原方程，有（原来偏导的几项变成了全微分）

+

dudt+u=x(t,x0)\frac{\rm d u}{\rm dt} + u = x(t,x_0) +

+

先解特征线方程，不难得到

+

x(t)=et(1+x0)−(1+t)x(t)=e^t(1+x_0)-(1+t) +

+

然后代入u的方程，解得但是我已经不会解ODE了

+

u(t)=1/2(x0+1)et+1/2(x0−1)e−t−tu(t) = 1/2(x_0+1)e^t + 1/2(x_0-1)e^{-t} -t +

+

同样特征线方程导出的结果，能够得到

+

x0=(x+t+1)e−t−1x_0 = (x+t+1)e^{-t} - 1 +

+

代入得到

+

u(x,t)=1/2(x+t+1)e−2t−e−t+1/2(x−t+1)u(x,t) = 1/2(x+t+1)e^{-2t} - e^{-t} + 1/2(x-t+1) +

+

齐次化原理

+

这大概是你们都不会学但是因为某位老师的恶趣味被塞进来的内容
+线性方程是可叠加的，具体看这个例子
+对于弦波动方程的两个解u1,u2u_1,u_2（这个方块算子是我的老师规定的，版权在他）

+

□ui=∂ttui−a2∂xxui=fi(x,t)\square u_i = \partial_{tt}u_i - a^2\partial_{xx}u_i = f_i(x,t) +

+

那么u=λ1u1+λ2u2u = \lambda_1 u_1 + \lambda_2 u_2就是

+

□u=λ1f1+λ2f2\square u = \lambda_1 f_1 + \lambda_2 f_2 +

+

的解

+

齐次化原理爷爷用线性叠加原理打掉一维波动方程初值问题

+

一维波动方程初值问题是

+

□u=f,u(x,0)=φ(x),∂tu(x,0)=ψ(x)\square u = f, u(x,0) = \varphi(x), \partial_t u(x,0) = \psi(x) +

+

由于线性叠加可行，我们对问题进行拆分

+

□u1=0,u1(x,0)=φ(x),∂tu1(x,0)=0\square u_1 = 0, u_1(x,0) = \varphi(x), \partial_t u_1(x,0) = 0 +

+

□u2=0,u2(x,0)=0,∂tu2(x,0)=ψ(x)\square u_2 = 0, u_2(x,0) = 0, \partial_t u_2(x,0) = \psi(x) +

+

□u3=f,u3(x,0)=0,∂tu3(x,0)=0\square u_3 = f, u_3(x,0) = 0, \partial_t u_3(x,0) = 0 +

+

原问题的解就是

+

u=u1+u2+u3u = u_1 + u_2 + u_3 +

+

齐次化原理是说，我们能够直接从u2u_2推导出u3u_3。u2u_2推u1u_1不是齐次化原理，但是是比较显然的
+总结一下就是下面的定理

+

定理

+

假设算子MM满足条件：u2=Mψ(x,t)u_2 = M_{\psi}(x,t)给出了u2u_2的解，那么u1,u3u_1,u_3可以分别被表示为

+

u1=∂tMψ(x,t),u3=∫0tMfτ(x,t−τ)dτu_1 = \partial_t M_{\psi}(x,t), u_3 = \int^t_0 M_{f_\tau}(x,t-\tau)\rm{d}\tau +

+

我们先不要去关心MM是什么，先看看这个定理怎么证明
+先用u2u_2推导u1u_1
+已知

+

(a)□Mφ=0, (b)Mφ(x,0)=0, (c)∂tMφ(x,0)=φ(x)(a)\square M_\varphi = 0,\space (b) M_\varphi(x,0) = 0,\space(c) \partial_t M_\varphi(x,0) = \varphi(x) +

+

希望推导出的是

+

(a′)□∂tMφ=0, (b′)∂tMφ(x,0)=φ(x), (c′)∂t∂tMφ(x,0)=0(a')\square \partial_t M_\varphi = 0,\space (b') \partial_t M_\varphi(x,0) = \varphi(x),\space(c') \partial_t \partial_t M_\varphi(x,0) = 0 +

+

(c)就是(b’)
+(a’)即

+

□(∂tMφ)=∂t□Mφ=0\square (\partial_t M_\varphi) = \partial_{t} \square M_\varphi = 0 +

+

(b’)即

+

∂ttMφ(x,0)=a2∂xxMφ(x,0)=0\partial_{tt} M_\varphi(x,0) = a^2\partial_{xx} M_\varphi(x,0) = 0 +

+

第二个等号利用了(b)
+接下来要证明u2⇒u3u_2 \Rarr u_3的部分

+

(a′′)□u3=f, (b′′)u3(x,0)=0, (c′′)∂tu3(x,0)=0(a'')\square u_3 = f, \space (b'') u_3(x,0) = 0, \space (c'') \partial_t u_3(x,0) = 0 +

+

不妨记

+

v(x,t)=∫0tMfτ(x,t−τ)dτv(x,t) = \int^t_0 M_{f_\tau}(x,t-\tau)\rm{d}\tau +

+

得到(b′′)v(x,0)=0(b'')v(x,0) = 0的结果

+

(c′′)∂tv(x,t)=∂t∫0tMfτ(x,t−τ)dτ=Mft(x,t−τ)∣τ=0+∫0t∂tMfτ(x,t−τ)dτ=∫0t∂tMfτ(x,t−τ)dτ\begin{align*} +(c'')\partial_t v(x,t) &= \partial_t \int^t_0 M_{f_\tau}(x,t-\tau)\rm{d}\tau \\ +&= M_{f_t}(x,t-\tau) |_{\tau = 0} + \int^t_0 \partial_t M_{f_\tau}(x,t-\tau)\rm{d}\tau \\ +&= \int^t_0 \partial_t M_{f_\tau}(x,t-\tau)\rm{d}\tau +\end{align*} +

+

显然有(c′′)∂t(x,0)=0(c'')\partial_t (x,0) = 0
+在上面导出的∂tv(x,t)\partial_t v(x,t)的基础上我们再求导

+

∂ttv(x,t)=∂t∫0t∂tMfτ(x,t−τ)dτ=∂tMft(x,0)+∫0t∂ttMfτ(x,t−τ)dτ=f(x,t)+∫0t∂ttMfτ(x,t−τ)dτ\begin{align*} +\partial_{tt} v(x,t) &= \partial_t \int_0^t \partial_t M_{f_\tau}(x,t-\tau)\rm{d}\tau\\ +&= \partial_t M_{f_t}(x,0) + \int^t_0 \partial_{tt} M_{f_\tau}(x,t-\tau)\rm{d}\tau \\ +&= f(x,t) + \int^t_0 \partial_{tt} M_{f_\tau}(x,t-\tau)\rm{d}\tau +\end{align*} +

+

最后一个等号使用了(c)
+那么

+

□v(x,t)=f(x,t)+∫0t∂ttMfτ(x,t−τ)dτ−a2∫0t∂xxMfτ(x,t−τ)dτ=f(x,t)+∫0t□Mfτ(x,t−τ)dτ=f(x,t)\begin{align*} +\square v(x,t) &= f(x,t) + \int^t_0 \partial_{tt} M_{f_\tau}(x,t-\tau)\rm{d}\tau - a^2\int^t_0 \partial_{xx} M_{f_\tau}(x,t-\tau)\rm{d}\tau \\ +&= f(x,t) + \int^t_0 \square M_{f_\tau}(x,t-\tau)\rm{d}\tau \\ +&= f(x,t) +\end{align*} +

+

第一个等号使用了求导和积分的次序交换，第二个等号使用了(a)
+证毕

+

一维初值问题

+

现在，我们只要得出u2u_2的解，就可以推导出原问题的解

+

先进行算子分解

+

□=∂tt−a2∂xx=(∂t+a∂x)(∂t−a∂x)\square = \partial_{tt} - a^2\partial_{xx} = (\partial_t + a\partial_x) (\partial_t - a\partial_x) +

+

我们假装算子分解是合理的，于是导出下面的结论

+

∂tu2−a∂xu2=v,u2(x,0)=0∂tv+a∂xv=0,v(x,0)=(∂tu2−a∂xu2)∣t=0=ψ(x)\partial_t u_2 - a \partial_x u_2 = v , u_2(x,0) = 0 \\ +\partial_t v + a \partial_x v = 0, v(x,0) = (\partial_t u_2 - a\partial_x u_2)|_{t=0} = \psi(x) +

+

这里将算子的复合看作“乘法”，其实是先进行算子分解结果右侧的运算得到v，然后再对v做左侧的运算

+

然后我们就能够使用特征线法对方程进行求解

+

先根据原有的条件我们得到

+

dxdt=advdt=∂tv+dxdt∂xv=∂tv+a∂xv=0v(x,t)=ψ(x−at)\rm \frac{dx}{dt} = a \\ +\rm \frac{dv}{dt} = \partial_t v + \frac{dx}{dt}\partial_x v =\rm \partial_t v + a\partial_x v = 0\\ +v(x,t) = \psi(x-at) +

+

再次使用特征线法

+

dxdt=−a,x(0)=x0⇒x0=x−atdu2dt=∂tu2+dxdt∂xu2=v(x,t)=ψ(x−at),u2(x(0),0)=0u2=∫0tψ(x0−2aτ)dτ=12a∫x−atx+atψ(ξ)dξ\rm \frac{dx}{dt} = -a, x(0) = x_0 \Rarr x_0 = x - at \\ +\rm \frac{du_2}{dt}= \partial_t u_2 + \frac{dx}{dt}\partial_x u_2 = v(x,t) = \psi(x-at), u_2(x(0),0) = 0\\ +u_2 = \int^t_0 \psi(x_0 - 2a\tau)\rm d\tau = \frac{1}{2a}\int^{x+at}_{x-at} \psi(\xi)\rm d \xi +

+

我们获得了所有的结果

+

u1=∂tMφ(x,t)=12a∂t(∫x−atx+atψ(ξ)dξ)=12a(aφ(x+at)−(−a)φ(x−at))=12(φ(x+at)−φ(x−at))\begin{align*} +u_1 = \partial_t M_{\varphi}(x,t) &= \frac{1}{2a}\partial_t(\int^{x+at}_{x-at} \psi(\xi)\rm d \xi) \\ +&= \frac{1}{2a}(a\varphi(x+at) - (-a)\varphi(x-at)) = \frac{1}{2}(\varphi(x+at) - \varphi(x-at)) +\end{align*} +

+

u3=∫0tMfτ(x,t−τ)dτ=12a∫0t∫x−atx+atf(ξ,τ)dξdτu_3 = \int^t_0 M_{f_\tau}(x,t-\tau){\rm d\tau} = \frac{1}{2a}\int^t_0\int^{x+at}_{x-at} f(\xi,\tau)\rm d \xi d\tau +

+

合并得到

+

u(x)=12(φ(x+at)−φ(x−at))+12∫x−atx+atψ(ξ)dξ+12a∫0t∫x−atx+atf(ξ,τ)dξdτu(x) += \frac{1}{2}(\varphi(x+at) - \varphi(x-at)) + \frac{1}{2}\int^{x+at}_{x-at}\psi(\xi){\rm d}\xi + \frac{1}{2a}\int^t_0\int^{x+at}_{x-at} f(\xi,\tau)\rm d \xi d\tau +

+

其实这个时候我都忘了原来的方程条件给了哪些了，我在这里再重抄一遍x

+

□u=f(x,t),u(x,0)=φ(x),∂tu(x,0)=ψ(x)\square u = f(x,t), u(x,0) = \varphi(x), \partial_t u(x,0) = \psi(x) +

+

f≡0f\equiv 0的时候，上面的公式又被称为D’ Alembert公式（我并不知道怎么念。。）

+

u(x,t)=12(φ(x+at)+φ(x−at))+12a∫x−atx+atψ(ξ)dξu(x,t) = \frac{1}{2}(\varphi(x+at)+\varphi(x-at))+\frac{1}{2a}\int^{x+at}_{x-at}\psi(\xi)\rm d\xi +

+

有意思的事情是，解在(x,t)(x,t)的数值仅仅依赖于x轴上区间[x−at,x+at][x-at,x+at]上的初值条件，而与其他地方的初值条件无关。区间[x−at,x+at][x-at,x+at]称为点(x,t)(x,t)的依赖区间

+

略过上述内容并不会对我们后续的学习产生太大影响

+
Author: zirno81
Link: http://blog.konpoku.top/2024/11/18/PDE1/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/11/20/EEEC2-1/index.html b/2024/11/20/EEEC2-1/index.html new file mode 100644 index 0000000..ee9d3db --- /dev/null +++ b/2024/11/20/EEEC2-1/index.html @@ -0,0 +1,229 @@ +电子电路与系统基础（2）：频率特性 | 正在施工中 + + + + + + + + + + + +

电子电路与系统基础（2）：频率特性

Created|Updated

先说结论：

+
    +
  • 数字门：延时、动态功耗
    • +
  • 放大器：高频增益下降、失去有源性、变得不稳定
    • +
+

晶体管高频电路模型

+

image-20241120193453675

+

然后glgg写了一大坨公式，给我看恶心了，我们跳过这一部分。

+

额，深思熟虑一下至少还是写一下节点电压法的方程列写方法吧

+

image-20241120194812216

+

在对角线上写出直接连接到该节点的导纳之和，然后其他地方写直接连接两个节点的导纳之和的负值

+

然后向量里面写通过源流入该节点的电流

+

然后就可以愉快的用Matlab来算这一坨了！

+

image-20241120195502173

+

感性分析一下

+

image-20241120195714916

+

首先是频率极小的时候，Cbe,Cbc,CceC_{be},C_{bc},C_{ce}三个寄生电容特别小，认为是开路的，不产生影响。但是CB,CC,CEC_B,C_C,C_E都开路了，CBC_B开路使得输入信号传不过来，CCC_C开路使得输出信号传不出去，CEC_E开路使得交流信号通过负反馈电阻，减小了增益。

+

然后是频率极大的时候，人为设置的三个外围电容短路，正常传递交流信号，但是Cbe,Cbc,CceC_{be},C_{bc},C_{ce}短路了，信号直接接地了，而且三极管组成的跨导器失去了控制作用，所以增益变小了

+

定量粗分析

+

分析五阶电路多少还是太悲惨了，所以我们粗略分析一下电路的频率特性

+

低频端近似分析

+

image-20241120201524763

+

rbr_b比较小，我们直接忽略，同样被忽略掉的还有三个寄生电容

+

然后我们再来单独分析三个外围电容

+

输入耦合电容的影响

+

image-20241120201700281

+

他具备典型的高通传递函数，所以我们直接写答案

+

Av=A0jωτB1+jωτBA_v = A_0 \frac{j \omega \tau_B}{1+j \omega \tau_B} +

+

其中A0A_0可以视作高频短路时候的增益，直接可以写出来

+

τB\tau_B则是输入耦合电容的时间常数，τB=(RB∥rbe+RS)CB\tau_B = (R_B \parallel r_{be}+R_S)C_B

+

输出耦合电容的影响

+

image-20241120202223224

+

同样是高通传递函数，直接写答案

+

TODO:稍微写一下

+

旁路电容的影响

+

image-20241120202419032

+

我操，这个难，

+
Author: zirno81
Link: http://blog.konpoku.top/2024/11/20/EEEC2-1/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/11/25/PDE2/index.html b/2024/11/25/PDE2/index.html new file mode 100644 index 0000000..e78e094 --- /dev/null +++ b/2024/11/25/PDE2/index.html @@ -0,0 +1,379 @@ +数理方程（二）波动方程的延续 | 正在施工中 + + + + + + + + + + + +

数理方程（二）波动方程的延续

Created|Updated

D’Alembert公式的解释

+

先复习一下D’Alembert公式

+

u(x,t)=12(φ(x+at)+φ(x−at))+12a∫x−atx+atψ(ξ)dξu(x,t) = \frac{1}{2}(\varphi(x+at)+\varphi(x-at))+\frac{1}{2a}\int^{x+at}_{x-at}\psi(\xi)\rm d \xi +

+

解在点(x,t)(x,t)的数值仅依赖于x轴上区间[x−at,x+at][x-at,x+at]内的初值条件，与其他地方的初值条件无关。我们把[x−at,x+at][x-at,x+at]叫做点(x,t)(x,t)的依赖区间

+

对于x轴上的区间[x1,x2][x_1,x_2]，在x1x_1作直线x=x1+atx=x_1+at，过x2x_2作直线x=x2−atx=x_2-at，他们和原来的区间围成了一个三角形区域，解在此区域中任意点的值都完全由区间[x1,x2][x_1,x_2]上的初值条件决定，与其他区域无关

+

反过来说，做直线x=x1−atx=x_1-at和x=x2+atx=x_2+at，则经过时间t后受到区间[x1,x2][x_1,x_2]上初值扰动的区域为

+

x1−at≤x≤x2+atx_1-at\leq x \leq x_2+at +

+

在此区域之外的波动不受[x1,x2][x_1,x_2]上的初始扰动的影响，称为此区域为[x1,x2][x_1,x_2]的影响区域

+

直线x=x0±x=x_0\pm
+TODO

+

一维半无界问题

+

我们之前的讨论都是基于整个x−tx-t平面进行讨论的，现在我们希望讨论更加现实一点的问题：如果有边界挡住了波的传播，会发生什么？

+

表达成正规数学语言的话，半无界边界问题可以表达为在区域Q‾={0≤x<∞,0≤t<∞}\overline{Q} = \{0 \leq x < \infty, 0 \leq t<\infty \}上有下面的约束条件

+

□u=f(x,t) ,0<x<∞, t>0u(x,0)=φ(x), 0≤x<∞∂tu(x,0)=ψ(x), 0≤x<∞u(0,t)=g(t),t>0\square u =f(x,t)\space,0 < x < \infty,\space t>0\\ +u(x,0) = \varphi (x),\space 0 \leq x < \infty\\ +\partial_t u(x,0) = \psi(x),\space 0 \leq x < \infty\\ +u(0,t) = g(t), t>0 +

+

第四条是新附加的边界条件，但是g(t)≠0g(t)\neq0的时候边界条件是非齐次的（我没看懂为什么非齐次，但是既然他这么说那就是吧，反之就是很复杂）。

+

不过我们可以考虑u=v+g(t)u = v+g(t)将问题转化为齐次情况

+

□v=f(x,t)−g′′(t) ,0<x<∞, t>0v(x,0)=φ(x)−g(0), 0≤x<∞∂tv(x,0)=ψ(x)−g′(0), 0≤x<∞v(0,t)=0,t>0\square v =f(x,t) - g''(t)\space,0 < x < \infty,\space t>0\\ +v(x,0) = \varphi (x) - g(0),\space 0 \leq x < \infty\\ +\partial_t v(x,0) = \psi(x)-g'(0),\space 0 \leq x < \infty\\ +v(0,t) = 0, t>0 +

+

因此我们直接默认只去解决(3)中g(t)≡0g(t)\equiv0的情况

+

g(t)≡0g(t)\equiv0其实帮助我们满足了奇延拓的前置条件，我们可以自然的将半无界问题延伸到简单的初值问题

+

f‾=f(x,t),x≥0 or−f(−x.t),x<0\overline{f} = f(x,t), x \geq 0 \space \mathrm{or} -f(-x.t) ,x < 0 +

+

我们把原来半个x轴上的问题拓宽到了整个x轴上，这样问题变成了一个一维初值问题
+那么就会有

+

{□u‾=f‾(x,t)u‾(x,0)=φ‾(x)∂tu‾(x,0)=ψ‾(x)\begin{cases} +\square \overline{u} = \overline{f}(x,t)\\ +\overline{u}(x,0) = \overline{\varphi}(x)\\ +\partial_t \overline{u}(x,0) = \overline{\psi}(x) +\end{cases} +

+

这里u(x,t)=u‾(x,t),x>=0u(x,t)=\overline{u}(x,t),x>=0
+对初值问题我们有显然的结论

+

u‾(x,t)=12(φ‾(x+at)+φ‾(x−at))+12a∫x−atx+atψ‾(ξ)dξ+12a∫−tt∫x−a(t−τ)x+a(t+τ)f‾(ξ,τ)dξdτ\overline{u}(x,t) = \frac{1}{2}(\overline{\varphi}(x+at)+\overline{\varphi}(x-at))+\frac{1}{2a}\int^{x+at}_{x-at}\overline{\psi}(\xi)\rm d \xi + \frac{1}{2a}\int^{t}_{-t}\int^{x+a(t+\tau)}_{x-a(t-\tau)}\overline{f}(\xi,\tau)\rm d \xi \rm d \tau +

+

更进一步将上面的解表达为φ,ψ,f\varphi,\psi,f的组合形式
+当x≥atx \geq at时解为

+

u(x,t))=12(φ(x+at)+φ(x−at))+12a∫x−atx+atψ(ξ)dξ+12a∫−tt∫x−a(t−τ)x+a(t+τ)f(ξ,τ)dξdτu(x,t)) = \frac{1}{2}(\varphi(x+at)+\varphi(x-at))+\frac{1}{2a}\int^{x+at}_{x-at}\psi(\xi)\rm d \xi + \frac{1}{2a}\int^{t}_{-t}\int^{x+a(t+\tau)}_{x-a(t-\tau)}f(\xi,\tau)\rm d \xi \rm d \tau +

+

当x<atx < at时解为

+

u(x,t))=12(φ(x+at)−φ(at−x))+12a∫at−xx+atψ(ξ)dξ+12a∫t−x/at∫x−a(t−τ)x+a(t+τ)f(ξ,τ)dξdτ+12a∫0t−x/a∫a(t−τ)−xx+a(t+τ)f(ξ,τ)dξdτu(x,t)) = \frac{1}{2}(\varphi(x+at)-\varphi(at-x))+\frac{1}{2a}\int^{x+at}_{at-x}\psi(\xi)\rm d \xi + \frac{1}{2a}\int^{t}_{t-x/a}\int^{x+a(t+\tau)}_{x-a(t-\tau)}f(\xi,\tau)\rm d \xi \rm d \tau + \frac{1}{2a}\int^{t-x/a}_{0} \int^{x+a(t+\tau)}_{a(t-\tau)-x}f(\xi,\tau)\rm d \xi \rm d \tau +

+

如果要保证解的连续性，那么应该有

+

φ(0)=g(0),ψ(0)=g′(0),g′′(0)−a2φ′′(0)=0\varphi(0) = g(0), \psi(0) = g'(0), g''(0) - a^2\varphi''(0) = 0 +

+

高维初值问题

+

大的要来了

+

大概的思路是这样的，先用球面平均法推导三维波动方程初值问题的解，再用降维法导出二维问题的解（听不懂啊啊啊）

+

三维的情况

+

三维初值问题表达如下

+

{□u=∂ttu−a2Δu=f(x,t),x∈R3u(x,0)=φ(x)∂tu(x,0)=ψ(x)\begin{cases} +\square u = \partial_{tt}u - a^2\Delta u = f(x,t), x \in \mathbb{R}^3\\ +u(x,0) = \varphi(x)\\ +\partial_t u(x,0)=\psi(x) +\end{cases} +

+

齐次化原理依然是满足的（因为齐次化原理部分的推导只和tt有关，没有涉及到xx的微积分操作）

+

因此问题被转换为下面的形式

+

□u2=0, u2(x,0)=0, ∂tu2(x,0)=ψ(x)\square u_2 = 0, \space u_2(x,0) = 0, \space \partial_t u_2(x,0) = \psi (x) +

+

高维情况下对x的微分情况复杂，不能~照抄~依葫芦画瓢使用前面的算子分解。这里使用球面平均法。

+

将问题转化到球坐标系下

+

1a2∂2u2∂t2=1r2∂∂r(r2∂u2∂r)+1r2sin⁡θ∂∂θ(sin⁡θ∂u2∂θ)+1r2sin⁡2θ∂2u2∂φ2\frac{1}{a^2}\frac{\partial^2u_2}{\partial t^2} = \frac{1}{r^2}\frac{\partial}{\partial r}(r^2 \frac{\partial u_2}{\partial r})+\frac{1}{r^2 \sin \theta}\frac{\partial}{\partial\theta}(\sin \theta \frac{\partial u_2}{\partial \theta}) + \frac{1}{r^2 \sin^2\theta}\frac{\partial^2 u_2}{\partial \varphi^2} +

+

在球对称假设（u2u_2和θ,φ\theta,\varphi无关）下我们有

+

ra2∂2u2∂t2=r∂2u2∂r2+2∂u2∂r\frac{r}{a^2}\frac{\partial^2u_2}{\partial t^2} = r\frac{\partial^2u_2}{\partial r^2}+2\frac{\partial u_2}{\partial r} +

+

进一步转换就是

+

ra2∂2u2∂t2=(r∂2u2∂r2+∂u2∂r)+∂u2∂r=∂∂r(r∂u2∂r)+∂u2∂r=∂2ru2∂r21a2∂2(ru2)∂t2=∂2(ru2)∂r2\frac{r}{a^2}\frac{\partial^2u_2}{\partial t^2} = (r\frac{\partial^2 u_2}{\partial r^2} + \frac{\partial u_2}{\partial r})+\frac{\partial u_2}{\partial r}=\frac{\partial }{\partial r}(r\frac{\partial u_2}{\partial r})+\frac{\partial u_2}{\partial r} = \frac{\partial^2 ru_2}{\partial r^2} +\\ +\frac{1}{a^2}\frac{\partial^2(ru_2)}{\partial t^2}=\frac{\partial^2(ru_2)}{\partial r^2} +

+

这其实就是一维半无界问题

+

但是实际问题没有球对称假设，于是我们考虑u2u_2以(x1,x2,x3)(x_1,x_2,x_3)为球心，以r>0r>0为半径的球面上的平均值（其实是引入了第四维r）。x固定时，平均值只和r,tr,t有关。如果转化出x为参数的形式，那么问题就得到了简化

+

考虑均值

+

u‾(r,t;x)=14πr2∬∣y∣=ru2(x+y,t)dS=14π∬∣y∣=1u2(x+ry,t)dω\overline{u}(r,t;x) = \frac{1}{4\pi r^2}\iint_{|y|=r}u_2(x+y,t){\rm d S} = \frac{1}{4\pi}\iint_{|y|=1}u_2(x+ry,t){\rm d \omega} +

+

上面的式子有两个重要结论

+

(1) Δx(ru‾(r,t;x))=∂2∂r2(ru‾(r,t;x))(2)lim⁡r→0u‾(r,t;x)=u2(x,t)\begin{align*} +&(1)\space\Delta_x(r\overline{u}(r,t;x)) = \frac{\partial^2}{\partial r^2}(r\overline{u}(r,t;x))\\ +&(2)\lim_{r \rightarrow 0}\overline{u}(r,t;x) = u_2(x,t) +\end{align*} +

+

第二个比较显然，第一个我不会推~~（第一个疑似也挺显然的但是我多元微积分学的一坨）~~

+

但是不管怎么说，我们能够继续推导(TODO:这里我不太会，回头再说)

+

+

+

∂2(ru‾)∂t2−a2∂2(ru‾)∂r2=0\frac{\partial^2(r\overline{u})}{\partial t^2} - a^2\frac{\partial^2(r\overline{u})}{\partial r^2} = 0 +

+

这里利用了原方程条件（懒得写了）

+

这是一个半无界问题，因为r≥0r\geq0，具体表示为（M=ru‾M = r\overline{u}）

+

∂ttM−a2∂rrM=0M(r,0;x)=0∂tM(r,0;x)=rψ‾(r;x)M(0,t;x)=0\begin{align*} +&\partial_{tt}M - a^2\partial_{rr}M = 0\\ +&M(r,0;x) = 0\\ +&\partial_{t}M(r,0;x) = r\overline{\psi}(r;x)\\ +&M(0,t;x)=0 +\end{align*} +

+

我们只关心r→0r \rightarrow 0附近的解，也就是(0≤r≤at)(0 \leq r \leq at)

+

M(r,t;x)=12a∫at−rat+rξψ‾(ξ;x)dξM(r,t;x) = \frac{1}{2a}\int_{at-r}^{at+r} \xi \overline{\psi} (\xi;x)\mathrm{d} \xi +

+

使用洛必达法则求极限（前面的极限！）

+

u2(x,t)=lim⁡r→0M(r,t;x)r=1aψ‾(at;x)=14πa2t∬∣y−x∣=atψ(y)dSu_{2}(x,t) = \lim_{ r \to 0 } \frac{M(r,t;x)}{r} =\frac{1}{a}\overline{\psi}(at;x)= \frac{1}{4\pi a^2 t}\iint_{|y-x|=at}\psi(y)\mathrm{d}S +

+

根据齐次化原理，我们导出了三维情况的Kirchhoff公式

+

u(x,t)=∂t(14πa2t∬∣y−x∣=atφ(y)dS)+14πa2t∬∣y−x∣=atψ(y)dS+∫0t(14πa2(t−τ)∬∣y−x∣=a(t−τ)f(y,τ)dS)dτu(x,t)=\partial_t \left( \frac{1}{4\pi a^2 t} \iint_{|y-x|=at} \varphi(y)\mathrm{d}S \right)+\frac{1}{4\pi a^2 t} \iint_{|y-x|=at} \psi(y)\mathrm{d}S+\int_{0}^{t} \left( \frac{1}{4\pi a^2 (t-\tau)} \iint_{|y-x|=a(t-\tau)} f(y,\tau)\mathrm{d}S \right) \mathrm{d}\tau +

+

我操，这是真不当人啊

+

进行降维

+

{□u=∂ttu−a2Δu=f(x,t),x∈R2u(x,0)=φ(x)∂tu(x,0)=ψ(x)\begin{cases} +\Box u = \partial_{tt}u - a^2\Delta u = f(x,t), x \in \mathbb{R}^2 \\ +u(x,0) = \varphi(x) \\ +\partial_{t}u(x,0) = \psi(x) +\end{cases} +

+

我们先说明一下为什么没办法直接用球面平均法
+将上面的方程化为极坐标，就有

+

1a2∂2u∂t2=1r∂∂r(r∂u∂r)+1r2∂2u∂θ2\frac{1}{a^2}\frac{\partial^2 u}{\partial t^2} = \frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial u}{\partial r}) + \frac{1}{r^2}\frac{\partial^2 u}{\partial \theta^2} +

+

（我操，copilot好聪明，一下给我全推完了）
+使用对称假设，uu与θ\theta无关，上面就有

+

ra2∂2u∂t2=∂2u∂r2+∂u∂r\frac{r}{a^2}\frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial r^2} + \frac{\partial u}{\partial r} +

+

等式右边的第二项少了系数2，没有办法依葫芦画瓢，所以我们采用降维法来将三维结论推广到二维
+之前的积分区域为球面

+

Sat(x)={y∈R3:∣y−x∣=at}S_{at}(x) = \{y \in \mathbb{R}^3:|y-x|=at\} +

+

现在我们希望把这个球面投影到二维平面上，即

+

Σat(x)={y∈R2:∣y−x∣≤at}\Sigma_{at}(x) = \{y \in \mathbb{R}^2:|y-x|\leq at\} +

+

然后我们就能套用Kirchhoff公式了~~（这个名字尤其不好打，反正我是记不住的）~~
+事实上可以使用下面的变换

+

dS=ata2t2−∣y−x∣2dy\mathrm{dS} = \frac{at}{\sqrt{ a^2t^2 - |y-x|^2 }}\mathrm{dy} +

+

这样我们就得到了二维波动方程的Poisson公式~~（认识的搞CG的人天天跟我念叨Poisson）~~

+

u(x,t)=12πa(∫∣y−x∣=atφ(y)a2t2−∣y−x∣2dy+∫∣y−x∣=atψ(y)a2t2−∣y−x∣2dy+∫0t∬∣y−x∣=a(t−τ)f(y,τ)a2(t−τ)2−∣y−x∣2dydτ)u(x,t) = \frac{1}{2\pi a}(\int_{|y-x|=at}\frac{\varphi(y)}{\sqrt{a^2t^2-|y-x|^2}}\mathrm{dy} + \int_{|y-x|=at}\frac{\psi(y)}{\sqrt{a^2t^2-|y-x|^2}}\mathrm{dy} + \int_{0}^{t}\iint_{|y-x|=a(t-\tau)}\frac{f(y,\tau)}{\sqrt{a^2(t-\tau)^2-|y-x|^2}}\mathrm{dy}\mathrm{d\tau}) +

+

发明数理方程的人真是神经病把

+

公式我懒得继续抄了，有一个比较有意思的事情是我们把f(x,t)f(x,t)置零（只考虑初值的影响），三维情况下波的传播是无后效性的，但是二维情况下由于积分区域的问题，波对某一点会一直产生影响（大概也许有可能会衰减，但是我不懂这个）

+

略过上述内容并不会对我们后续的学习产生太大影响

+
Author: zirno81
Link: http://blog.konpoku.top/2024/11/25/PDE2/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/11/27/EEEC2-3/index.html b/2024/11/27/EEEC2-3/index.html new file mode 100644 index 0000000..be30df3 --- /dev/null +++ b/2024/11/27/EEEC2-3/index.html @@ -0,0 +1,244 @@ +电子电路与系统基础（2）：（三）负反馈网络 | 正在施工中 + + + + + + + + + + + +

电子电路与系统基础（2）：（三）负反馈网络

Created|Updated

以非理想小信号放大器为例

+

image.png

+

输入输出端口负载和原来抽象出来的电阻复合了，RER_{E}在强大的−gmrinrout-g_{m}r_{in}r_{out}面前基本上可以忽略不计，稍微改写一下就变成

+

image.png

+

现在我们来看看什么时候负反馈放大器能够被看作单向网络

+

image.png

+

image.png

+

这里单向网络传递函数的的解释比较基础，重述一遍就是：
+信号源先因为内阻和y11y_{11}被分压，然后由本征跨导增益变为−i2-i_{2}电流，最后由y22y_{22}和负载的电阻作用变为电压，从右到左对应乘上去的项

+

单向化条件已经得到了，拆分一下就是

+

image.png

+

然后glgg在这里举例做了一堆计算，反之就是说xx条件满足上面说的单向化条件，这里有一个比较重要的二级结论是

+

image.png

+

routfr_{outf}稍微误差大一点，不过对于平时接的小电阻来说差不多。

+

但是这降低了增益

+

image.png

+

这里也有重要的估算结论，反之多记一下（记不住啊）

+

想要提高增益就需要采取折中方案，用旁路电容降低交流负反馈电阻

+

image.png

+

负反馈减弱反映在对增益估算的误差增大上

+

我们可以把负反馈的结论推广到以其他形式连接的反馈网络上，其中会有

+

image.png

+

分析流程如下

+

image.png

+

image.png

+

通用性的结论如下

+

image.png

+

由于公共地的存在，有口诀：是一个点是并联，不是一个点就是串联

+

image.png

+

用运放举例就是

+

image.png

+

image.png

+

简化电路，在输出端加测试电压，输入端短路测电流

+

image.png

+

得到了结论

+

求输入输出阻抗的话，纯数学流程是这样的：

+

image.png

+

先分别求两个网络的yy参量，然后并并连接yy相加，再求逆

+

但是如果y12=0y_{12}=0，求逆会出大问题，（g了）
+所以要想办法用电路的方式来分析

+

image.png

+

单独来研究开环放大器

+

image.png

+

经典口诀：放大网络画一遍，反馈网络画两遍。

+

所以对于前面的运放反馈网络，变成下面这样

+

image.png

+

image.png

+

然后我们就可以来看开环放大器的阻抗了

+

image.png

+

然后把它搞成闭环

+

image.png

+

image.png

+

先求出开环放大器的网络参量，直接除以(1+T)(1+T)就是闭环放大器的网络参量

+
Author: zirno81
Link: http://blog.konpoku.top/2024/11/27/EEEC2-3/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/11/27/PDE3/index.html b/2024/11/27/PDE3/index.html new file mode 100644 index 0000000..120fd53 --- /dev/null +++ b/2024/11/27/PDE3/index.html @@ -0,0 +1,338 @@ +数理方程（3）：热传导方程和积分变换初步 | 正在施工中 + + + + + + + + + + + +

数理方程（3）：热传导方程和积分变换初步

Created|Updated

一维初值问题

+

解方程

+

考虑一维热传导方程初值问题

+

∂tu−a2∂xxu=f(x,t)u(x,0)=φ(x)\partial_{t} u - a^2\partial_{x x}u = f(x,t)\\ +u(x,0) = \varphi (x) +

+

对u，在x上做傅立叶变换

+

u(x,t)→Fu^(x,t),∂xxu^=(iω)2u^u(x,t) \stackrel{\mathcal{F}}{\rightarrow} \hat{u}(x,t), \partial_{x x}\hat{u} = (i \omega)^2\hat{u} +

+

那么偏微分方程被我们转换成为了

+

∂tu^+a2ω2u^=f^(ω,t)u^(x,0)=φ^(x)\partial_{t} \hat{u} + a^2 \omega^2 \hat{u} = \hat{f}(\omega,t)\\ +\hat{u}(x,0) = \hat{\varphi}(x) +

+

这是一个PDE，能够解得

+

u^(ω,t)=φ^e−a2ω2t+∫0tf^(ω,τ)e−a2ω2(t−τ)dτ\hat{u}(\omega,t) = \hat{\varphi}e^{ -a^2 \omega^{2}t }+ \int^t_{0}\hat{f}(\omega,\tau)e^{ -a^{2}\omega^{2}(t-\tau) }\mathrm{d\tau} +

+

对上式做傅立叶逆变换，那么有

+

u(x,t)=F−1[φe−a2ω2t^]+∫0tF−1[f^(ω,τ),e−a2ω2(t−τ)]u(x,t) = \mathcal{F}^{-1}[\hat{\varphi e^{ -a^{2}\omega^{2}t }}]+\int^t_{0}\mathcal{F}^{-1}[\hat{f}(\omega,\tau),e^{ -a^{2}\omega^{2}(t-\tau) }] +

+

为了化简上面的式子，我们采用傅立叶变换的卷积性质

+

F[f1(x)∗f2(x)]=2πf1^(ω)f2^(ω)F−1[f1^(ω)f2(ω)^]=12πf1(x)∗f2(x)\mathcal{F}[f_{1}(x)*f_{2}(x)] = \sqrt{ 2\pi }\hat{f_{1}}(\omega)\hat{f_{2}}(\omega)\\ +\mathcal{F}^{-1}[\hat{f_{1}}(\omega)\hat{f_{2}(\omega)}] = \frac{1}{\sqrt{ 2\pi }}f_{1}(x)*f_{2}(x) +

+

我们进行化简

+

u(x,t)=φ(x)2aπt∗e−x2/4a2t+∫0tf(x,τ)2aπ(t−τ)∗e−x2/4a2(t−τ)dτu(x,t) = \frac{\varphi(x)}{2a \sqrt{ \pi t }} * e^{ -x^2/4a^{2}t } + \int^t_{0} \frac{f(x,\tau)}{2a\sqrt{ \pi(t-\tau) }}*e^{ -x^2/4a^2(t-\tau) }\mathrm{d\tau} +

+

约定Poisson核由下面的式子给出

+

K(x,t)={12aπte−x2/4a2t,t>00,t≤0K(x,t) = \begin{cases} +\frac{1}{2a\sqrt{ \pi t }e^{ -x^{2}/4a^{2}t }},&t>0\\ \\ +0,&t \leq 0 +\end{cases} +

+

上面的式子就表达为

+

u(x,t)=∫−∞∞K(x−ξ,t)φ(ξ) dξ+∫0t∫−∞∞K(x−ξ,t−τ)f(ξ,τ) dξdτu(x,t) = \int_{-\infty}^{\infty} K(x-\xi,t)\varphi(\xi) \, d\xi + \int^t_{0}\int_{-\infty}^{\infty} K(x-\xi,t-\tau)f(\xi,\tau) \, d\xi d\tau +

+

K(x,t)K(x,t)满足基本的一点性质

+

lim⁡t→0+K(x,t)=δ(x)\lim_{ t \to 0^+ } K(x,t) = \delta(x) +

+

认为K(x,t)K(x,t)在广义函数意义下满足初值问题

+

∂tv−a2∂xxv=0,v(x,0)=δ(x)\partial_{t}v - a^2\partial_{x x}v = 0,v(x,0)=\delta(x) +

+

考虑Poisson核的好处是有下面的结论

+

∂xx(f1(x)∗f2(x))=∂xx(∫−∞∞f1(ξ)f2(x−ξ) dξ)=∫−∞∞f1(ξ)∂xxf2(x−ξ) dξ=f1(x)∗(∂xxf2(x))\partial_{x x}(f_{1}(x) * f_{2}(x)) = \partial_{x x}\left( \int_{-\infty}^{\infty} f_{1}(\xi)f_{2}(x-\xi) \, d\xi \right) = \int_{-\infty}^{\infty} f_{1}(\xi)\partial_{x x}f_{2}(x-\xi) \, d\xi = f_{1}(x)*(\partial_{x x}f_{2}(x)) +

+

考虑Poisson核对应的初值问题和φ(x)\varphi(x)的卷积

+

φ∗(∂tv−a2∂xxv)=∂t(φ∗v)−a2∂xx(φ∗v)=0φ(x)∗v(x,0)=φ(x)∗δ(x)=φ(x)\varphi * (\partial_{t}v - a^2\partial_{xx}v) = \partial_{t}(\varphi * v) - a^{2}\partial_{x x}(\varphi * v) = 0\\ +\varphi(x)*v(x,0) = \varphi(x)*\delta(x) = \varphi(x) +

+

即函数u(x,t)=φ(x)∗K(x,t)u(x,t) = \varphi(x)*K(x,t)满足初值问题

+

∂tu−a2∂xxu=0,u(x,0)=φ(x)\partial_{t}u - a^{2}\partial_{x x}u = 0, u(x,0) = \varphi(x) +

+

惊喜的发现，我们得到了完全问题的部分解
+所以其实热传导方程的求解很简单~~（比之前的波动方程高到不知道哪里去了）~~
+先求解初值为点热源的齐次热传导方程得到K(x,t)K(x,t)，再将初值φ(x)\varphi(x)对KK做卷积得到解。（点热源听起来挺像图形学里面的点光源的）
+换句话说，我们其实求的是如下基本解问题

+

∂tu−a2∂xxu=δ(x−ξ,t−τ),u(x,0)=0\partial_{t} u - a^{2}\partial_{x x}u = \delta(x-\xi,t-\tau), u(x,0)=0 +

+

解为

+

Γ(x,t;ξ,τ)=K(x−ξ,t−τ)\Gamma(x,t;\xi,\tau) = K(x-\xi,t-\tau) +

+

观察Poisson公式我们就能看到

+

u(x,t)=∫−∞∞K(x−ξ,t)φ(ξ) dξ+∫0t∫−∞∞K(x−ξ,t−τ)f(ξ,τ) dξdτu(x,t) = \int_{-\infty}^{\infty} K(x-\xi,t)\varphi(\xi) \, d\xi + \int^t_{0}\int_{-\infty}^{\infty} K(x-\xi,t-\tau)f(\xi,\tau) \, d\xi d\tau +

+

其实一维热传导方程初值问题，就是在解K(x,t)K(x,t)或者基本解Γ(x,t;ξ,τ)\Gamma(x,t;\xi,\tau)，非齐次部分f(x,t)f(x,t)可以搬用齐次化原理的方法

+

重要性质

+

Poisson公式其实有一些很有意思的性质

+
    +
  • 保持奇偶性和周期性质：方程的解保持了φ\varphi的奇偶和周期性质
    • +
  • 无限传播速度：考虑初值φ(x)\varphi(x)仅在小段(x0−δ,x0+δ)(x_{0}-\delta,x_{0}+\delta)上不为0，φ(x)>0\varphi(x)>0，那么t>0t>0以后，杆上各点的温度为
    • +
+

u(x,t)=∫−∞∞K(x−ξ,t)φ(ξ) dξ=∫−δδK((x−x0)−η,t)φ(x0+η) dη>0u(x,t) = \int_{-\infty}^{\infty} K(x-\xi,t)\varphi(\xi) \, d\xi = \int_{-\delta}^{\delta} K((x-x_{0})-\eta,t)\varphi(x_{0}+\eta) \, d \eta > 0 +

+
    +
  • 可以说是温度一瞬间传递到杆上每一点，这是由于我们引入热传导方程的时候，使用的对实际物理情况近似的假设所导致的~~（感性理解，反正我不会推）~~
    • +
  • 无穷次可微，我懒得写了，反之就是有
    • +
+

∂k+lu∂xk∂tl=∫−∞∞∂k+lK(x−ξ,t)∂xk∂tlφ(ξ) dξ\frac{\partial^{k+l}u}{\partial x^k\partial t^l}=\int_{-\infty}^{\infty} \frac{\partial^{k+l}K(x-\xi,t)}{\partial x^k\partial t^l}\varphi(\xi) \, d\xi +

+

高维初值问题

+

傅立叶变换非常屌有很好的性质，对单个变量的傅立叶变换不会影响其他变量（也就是说我可以把其他变量的导数和积分的位置换来换去），那么对于高维问题

+

∂tu−a2Δu=f(x,t),(x,t)∈Rn×(0,∞)u(x,0)=φ(x),x∈Rn\partial_{t} u - a^{2}\Delta u = f(x,t), (x,t)\in \mathbb{R}^n \times (0,\infty)\\ +u(x,0) = \varphi(x), x \in \mathbb{R}^n +

+

直接用多维傅立叶变换求解得到

+

u(x,y,z,t)=∭R3K(x−ξ,y−η,z−ζ,t)φ(ξ,η,ζ)dξdηdζ+∫0t∭R3K(x−ξ,y−η,t−τ)f(ξ,η,ζ,τ)dξdηdζ dτ u(x,y,z,t) = \iiint_{\mathbb{R^3}}K(x-\xi,y-\eta,z-\zeta,t)\varphi(\xi,\eta,\zeta)\mathrm{d\xi d \eta d\zeta}\\+\int_{0}^{t} \iiint_{\mathbb{R}^3}K(x-\xi,y-\eta,t-\tau)f(\xi,\eta,\zeta,\tau)\mathrm{d\xi d \eta d \zeta} \, d\tau +

+

扩展问题

+

对流扩散方程为

+

∂tu+a∂xu=v∂xxu,x∈R,t>0\partial_{t} u + a\partial_{x}u = v\partial_{x x}u, x\in \mathbb{R}, t>0 +

+

其实是在说扩散和对流同时进行。当a≫va \gg v的时候，叫做对流占优问题，反之wh说这个东西用的很多。

+

积分变换再举例

+

TODO

+
Author: zirno81
Link: http://blog.konpoku.top/2024/11/27/PDE3/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/12/04/EEEC2-4/index.html b/2024/12/04/EEEC2-4/index.html new file mode 100644 index 0000000..e00a2da --- /dev/null +++ b/2024/12/04/EEEC2-4/index.html @@ -0,0 +1,212 @@ +电子电路与系统基础（2）：（四）正反馈和负阻 | 正在施工中 + + + + + + + + + + + +

电子电路与系统基础（2）：（四）正反馈和负阻

Created|Updated

运放正反馈

+

image.png

+

这个实验做了很多，理解应该是比较深刻了的
+正反馈存在解可能非唯一的问题。

+

image.png

+

在蓝色虚线区工作是不稳定的，物理上无法测出该区域，所以测量得到的是滞回曲线

+

正反馈和负反馈同时添加（通过负反馈让电路呆在线性区）

+

image.png

+

显然有1>F，负反馈占优，虚短虚断得到vOUT=0。
+在线性区的时候，用加流求压求端口电阻得到负电阻（不能用加压求流）

+

image.png

+

有一定的约束

+

image.png

+

在饱和区的时候

+

image.png

+

同样加流求压，能够得到限制条件，以及电路抽象为戴维南源

+

image.png

+

看输入输出电压关系，每个电流都有唯一对应电压，认为是流控器件，测量的时候只能加测试电流。这里负反馈大于正反馈

+

image.png

+

加压的时候正反馈大于负反馈，运放呆不在线性区，

+

电子系你妈死了

+
Author: zirno81
Link: http://blog.konpoku.top/2024/12/04/EEEC2-4/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/12/04/PDE4/index.html b/2024/12/04/PDE4/index.html new file mode 100644 index 0000000..3cb9c6f --- /dev/null +++ b/2024/12/04/PDE4/index.html @@ -0,0 +1,244 @@ +数理方程（4）：位势方程和Green函数法 | 正在施工中 + + + + + + + + + + + +

数理方程（4）：位势方程和Green函数法

Created|Updated

方程形式

+

位势方程主要是说

+

−Δu=f-\Delta u=f +

+

其中Δ=∑i=1d∂2∂xi2\Delta = \sum^{d}_{i=1} \frac{\partial^2}{\partial x_{i}^2}是Laplace算子，d为空间维数，f是源项，当f=0的时候方程又被称为Laplace方程或者调和方程。

+

Green公式和基本解

+

Green公式是说：

+

证明：由于

+

uΔv=u(∇⋅∇v)=∇⋅(u∇v)−∇u⋅∇vu \Delta v = u(\nabla \cdot \nabla v) = \nabla \cdot(u \nabla v) - \nabla u \cdot \nabla v +

+

（直接拆开就能得到）
+所以有

+

uΔv−vΔu=∇⋅(u∇v−v∇u)u \Delta v - v \Delta u = \nabla \cdot(u \nabla v - v \nabla u) +

+

对两边在Ω\Omega进行积分，再利用Green公式

+

∬Ω∇⋅dx=∫∂Ωu⋅ndl\iint_{\Omega} \nabla \cdot \mathrm{dx} = \int_{\partial \Omega}u \cdot n \mathrm{d}l +

+

得到证明。

+

利用上面的结论可以得到二维Laplace方程的基本解为

+

Γ(x,y;ξ,η)=12πln⁡1(x−ξ)2+(y−η)2\Gamma(x,y;\xi,\eta)= \frac{1}{2\pi}\ln\frac{1}{\sqrt{ (x-\xi)^2 + (y-\eta)^{2} }} +

+

证明：
+我们把解带入Laplace方程在数学上的严格形式
+由于Γ\Gamma在(x,y)=(ξ,η)(x,y) = (\xi,\eta)时有奇性，因此考虑区域

+

Ωϵ=(x,y)∈R2∣ϵ\Omega_{\epsilon} = {(x,y) \in \mathbb{R}^2 | \epsilon} +

+

对任意测试函数

+

φ(x,y)=−∬R2Γ(x,y;ξ,η)Δφdxdy=−lim⁡ϵ→0+∬ΩϵΓ(x,y;ξ,η)Δdxdy=−lim⁡ϵ→0+∬ΩϵφΔΓ(x,y;ξ,η)dxdy+lim⁡ϵ→0+∫∂Ωϵ(φ∂Γ∂n−Γ∂φ∂n)dl\begin{align} +\varphi(x,y) &= -\iint_{\mathbb{R}^{2}}\Gamma(x,y;\xi,\eta)\Delta \varphi \mathrm{dxdy} = -\lim_{ \epsilon \to 0^+ }\iint_{\Omega_{\epsilon}}\Gamma(x,y;\xi,\eta)\Delta \mathrm{dxdy} \\ +&=-\lim_{ \epsilon \to 0^+ } \iint_{\Omega_{\epsilon}}\varphi \Delta \Gamma(x,y;\xi,\eta)\mathrm{dxdy}+\lim_{ \epsilon \to 0^+ } \int_{\partial \Omega_{\epsilon}} \left( \varphi\frac{\partial\Gamma}{\partial n} - \Gamma\frac{\partial\varphi}{\partial n} \right)\mathrm{dl} +\end{align} +

+

在解决位势方程之前，我们还要引入一个简单定理作为基础
+设∂Ω\partial \Omega分段光滑，u∈C2(Ω)∩C1(Ω‾)u \in C^2(\Omega) \cap C^1(\overline{\Omega})，有

+

u(ξ,η)=−∬ΩΓΔudxdy+∫∂Ω(Γ∂u∂n−∂Γ∂nu)u(\xi,\eta) = -\iint_{\Omega}\Gamma \Delta u \mathrm{dxdy} + \int_{\partial \Omega}\left( \Gamma \frac{ \partial u }{ \partial n } - \frac{ \partial \Gamma }{ \partial n } u \right) +

+

证明：直接用Green公式有

+

∬Ω(uΔΓ−ΓΔu)dxdy=∫∂Ω(u∂Γ∂n−Γ∂u∂n)dl\iint_{\Omega}(u \Delta \Gamma - \Gamma \Delta u)\mathrm{dxdy} = \int_{\partial \Omega}\left( u \frac{ \partial \Gamma }{ \partial n } - \Gamma \frac{ \partial u }{ \partial n } \right)\mathrm{d l} +

+

Green函数

+

引入辅助函数g(x,y;ξ,η)g(x,y;\xi,\eta)，使得

+

Δ(x,y)g(x,y;ξ,η)=0\Delta_{(x,y)} g(x,y;\xi,\eta)=0 +

+
Author: zirno81
Link: http://blog.konpoku.top/2024/12/04/PDE4/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/2024/12/04/PDE5/index.html b/2024/12/04/PDE5/index.html new file mode 100644 index 0000000..3db67bc --- /dev/null +++ b/2024/12/04/PDE5/index.html @@ -0,0 +1,192 @@ +数理方程（五）分离变量法 | 正在施工中 + + + + + + + + + + + +

数理方程（五）分离变量法

Created|Updated

终于讲到大杀器了，为什么不早点讲啊

+
Author: zirno81
Link: http://blog.konpoku.top/2024/12/04/PDE5/
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
\ No newline at end of file diff --git a/CNAME b/CNAME new file mode 100644 index 0000000..c3c3e29 --- /dev/null +++ b/CNAME @@ -0,0 +1 @@ +blog.konpoku.top \ No newline at end of file diff --git a/archives/2023/10/index.html b/archives/2023/10/index.html new file mode 100644 index 0000000..e6a3d25 --- /dev/null +++ b/archives/2023/10/index.html @@ -0,0 +1,208 @@ +October 2023 | 正在施工中 + + + + + + + +

October 2023

All Articles - 1
2023
THUCTF 2023 部分 Writeup
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
+
+ + Archives + +
+
Website Info
Article Count :
12
Last Update :
\ No newline at end of file diff --git a/archives/2023/index.html b/archives/2023/index.html new file mode 100644 index 0000000..1d8a6c5 --- /dev/null +++ b/archives/2023/index.html @@ -0,0 +1,208 @@ +2023 | 正在施工中 + + + + + + + +

2023

All Articles - 1
2023
THUCTF 2023 部分 Writeup
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
+
+ + Archives + +
+
Website Info
Article Count :
12
Last Update :
\ No newline at end of file diff --git a/archives/2024/05/index.html b/archives/2024/05/index.html new file mode 100644 index 0000000..bba3a3b --- /dev/null +++ b/archives/2024/05/index.html @@ -0,0 +1,208 @@ +May 2024 | 正在施工中 + + + + + + + +

May 2024

All Articles - 1
2024
清华电子系数算 OJ 通关指北
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
+
+ + Archives + +
+
Website Info
Article Count :
12
Last Update :
\ No newline at end of file diff --git a/archives/2024/11/index.html b/archives/2024/11/index.html new file mode 100644 index 0000000..a6a5ad1 --- /dev/null +++ b/archives/2024/11/index.html @@ -0,0 +1,208 @@ +November 2024 | 正在施工中 + + + + + + + +

November 2024

avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
+
+ + Archives + +
+
Website Info
Article Count :
12
Last Update :
\ No newline at end of file diff --git a/archives/2024/12/index.html b/archives/2024/12/index.html new file mode 100644 index 0000000..d1adc43 --- /dev/null +++ b/archives/2024/12/index.html @@ -0,0 +1,208 @@ +December 2024 | 正在施工中 + + + + + + + +

December 2024

avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
+
+ + Archives + +
+
Website Info
Article Count :
12
Last Update :
\ No newline at end of file diff --git a/archives/2024/index.html b/archives/2024/index.html new file mode 100644 index 0000000..8746fd0 --- /dev/null +++ b/archives/2024/index.html @@ -0,0 +1,208 @@ +2024 | 正在施工中 + + + + + + + +

2024

avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
+
+ + Archives + +
+
Website Info
Article Count :
12
Last Update :
\ No newline at end of file diff --git a/archives/2024/page/2/index.html b/archives/2024/page/2/index.html new file mode 100644 index 0000000..ff6e5a2 --- /dev/null +++ b/archives/2024/page/2/index.html @@ -0,0 +1,208 @@ +2024 | 正在施工中 + + + + + + + +

2024

All Articles - 11
2024
清华电子系数算 OJ 通关指北
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
+
+ + Archives + +
+
Website Info
Article Count :
12
Last Update :
\ No newline at end of file diff --git a/archives/index.html b/archives/index.html new file mode 100644 index 0000000..3068bb6 --- /dev/null +++ b/archives/index.html @@ -0,0 +1,208 @@ +Archives | 正在施工中 + + + + + + + +

Archives

avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
+
+ + Archives + +
+
Website Info
Article Count :
12
Last Update :
\ No newline at end of file diff --git a/archives/page/2/index.html b/archives/page/2/index.html new file mode 100644 index 0000000..3786711 --- /dev/null +++ b/archives/page/2/index.html @@ -0,0 +1,208 @@ +Archives | 正在施工中 + + + + + + + +

Archives

All Articles - 12
2024
清华电子系数算 OJ 通关指北
2023
THUCTF 2023 部分 Writeup
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
+
+ + Archives + +
+
Website Info
Article Count :
12
Last Update :
\ No newline at end of file diff --git a/css/bounce.css b/css/bounce.css new file mode 100644 index 0000000..39ef9b2 --- /dev/null +++ b/css/bounce.css @@ -0,0 +1,230 @@ +.pace { + width: 140px; + height: 300px; + position: fixed; + top: -90px; + right: -20px; + z-index: 2000; + -webkit-transform: scale(0); + -moz-transform: scale(0); + -ms-transform: scale(0); + -o-transform: scale(0); + transform: scale(0); + opacity: 0; + -webkit-transition: all 2s linear 0s; + -moz-transition: all 2s linear 0s; + transition: all 2s linear 0s; +} + +.pace.pace-active { + -webkit-transform: scale(.25); + -moz-transform: scale(.25); + -ms-transform: scale(.25); + -o-transform: scale(.25); + transform: scale(.25); + opacity: 1; +} + +.pace .pace-activity { + width: 140px; + height: 140px; + border-radius: 70px; + background: #006ba8; + position: absolute; + top: 0; + z-index: 1911; + -webkit-animation: pace-bounce 1s infinite; + -moz-animation: pace-bounce 1s infinite; + -o-animation: pace-bounce 1s infinite; + -ms-animation: pace-bounce 1s infinite; + animation: pace-bounce 1s infinite; +} + +.pace .pace-progress { + position: absolute; + display: block; + left: 50%; + bottom: 0; + z-index: 1910; + margin-left: -30px; + width: 60px; + height: 75px; + background: rgba(20, 20, 20, .1); + box-shadow: 0 0 20px 35px rgba(20, 20, 20, .1); + border-radius: 30px / 40px; + -webkit-transform: scaleY(.3) !important; + -moz-transform: scaleY(.3) !important; + -ms-transform: scaleY(.3) !important; + -o-transform: scaleY(.3) !important; + transform: scaleY(.3) !important; + -webkit-animation: pace-compress .5s infinite alternate; + -moz-animation: pace-compress .5s infinite alternate; + -o-animation: pace-compress .5s infinite alternate; + -ms-animation: pace-compress .5s infinite alternate; + animation: pace-compress .5s infinite alternate; +} + +@-webkit-keyframes pace-bounce { + 0% { + top: 0; + -webkit-animation-timing-function: ease-in; + } + 40% {} + 50% { + top: 140px; + height: 140px; + -webkit-animation-timing-function: ease-out; + } + 55% { + top: 160px; + height: 120px; + border-radius: 70px / 60px; + -webkit-animation-timing-function: ease-in; + } + 65% { + top: 120px; + height: 140px; + border-radius: 70px; + -webkit-animation-timing-function: ease-out; + } + 95% { + top: 0; + -webkit-animation-timing-function: ease-in; + } + 100% { + top: 0; + -webkit-animation-timing-function: ease-in; + } +} + +@-moz-keyframes pace-bounce { + 0% { + top: 0; + -moz-animation-timing-function: ease-in; + } + 40% {} + 50% { + top: 140px; + height: 140px; + -moz-animation-timing-function: ease-out; + } + 55% { + top: 160px; + height: 120px; + border-radius: 70px / 60px; + -moz-animation-timing-function: ease-in; + } + 65% { + top: 120px; + height: 140px; + border-radius: 70px; + -moz-animation-timing-function: ease-out;} + 95% { + top: 0; + -moz-animation-timing-function: ease-in; + } + 100% {top: 0; + -moz-animation-timing-function: ease-in; + } +} + +@keyframes pace-bounce { + 0% { + top: 0; + animation-timing-function: ease-in; + } + 50% { + top: 140px; + height: 140px; + animation-timing-function: ease-out; + } + 55% { + top: 160px; + height: 120px; + border-radius: 70px / 60px; + animation-timing-function: ease-in; + } + 65% { + top: 120px; + height: 140px; + border-radius: 70px; + animation-timing-function: ease-out; + } + 95% { + top: 0; + animation-timing-function: ease-in; + } + 100% { + top: 0; + animation-timing-function: ease-in; + } +} + +@-webkit-keyframes pace-compress { + 0% { + bottom: 0; + margin-left: -30px; + width: 60px; + height: 75px; + background: rgba(20, 20, 20, .1); + box-shadow: 0 0 20px 35px rgba(20, 20, 20, .1); + border-radius: 30px / 40px; + -webkit-animation-timing-function: ease-in; + } + 100% { + bottom: 30px; + margin-left: -10px; + width: 20px; + height: 5px; + background: rgba(20, 20, 20, .3); + box-shadow: 0 0 20px 35px rgba(20, 20, 20, .3); + border-radius: 20px / 20px; + -webkit-animation-timing-function: ease-out; + } +} + +@-moz-keyframes pace-compress { + 0% { + bottom: 0; + margin-left: -30px; + width: 60px; + height: 75px; + background: rgba(20, 20, 20, .1); + box-shadow: 0 0 20px 35px rgba(20, 20, 20, .1); + border-radius: 30px / 40px; + -moz-animation-timing-function: ease-in; + } + 100% { + bottom: 30px; + margin-left: -10px; + width: 20px; + height: 5px; + background: rgba(20, 20, 20, .3); + box-shadow: 0 0 20px 35px rgba(20, 20, 20, .3); + border-radius: 20px / 20px; + -moz-animation-timing-function: ease-out; + } +} + +@keyframes pace-compress { + 0% { + bottom: 0; + margin-left: -30px; + width: 60px; + height: 75px; + background: rgba(20, 20, 20, .1); + box-shadow: 0 0 20px 35px rgba(20, 20, 20, .1); + border-radius: 30px / 40px; + animation-timing-function: ease-in; + } + 100% { + bottom: 30px; + margin-left: -10px; + width: 20px; + height: 5px; + background: rgba(20, 20, 20, .3); + box-shadow: 0 0 20px 35px rgba(20, 20, 20, .3); + border-radius: 20px / 20px; + animation-timing-function: ease-out; + } +} \ No newline at end of file diff --git a/css/hbe.style.css b/css/hbe.style.css new file mode 100644 index 0000000..060f1f8 --- /dev/null +++ b/css/hbe.style.css @@ -0,0 +1,749 @@ +.hbe, +.hbe:after, +.hbe:before { + -webkit-box-sizing: border-box; + -moz-box-sizing: border-box; + box-sizing: border-box; +} + +.hbe-container{ + margin: 0 auto; + overflow: hidden; +} +.hbe-content { + text-align: center; + font-size: 150%; + padding: 1em 0; +} + +.hbe-input { + position: relative; + z-index: 1; + display: inline-block; + margin: 1em; + width: 80%; + min-width: 200px; + vertical-align: top; +} + +.hbe-input-field { + line-height: normal; + font-size: 100%; + margin: 0; + position: relative; + display: block; + float: right; + padding: 0.8em; + width: 60%; + border: none; + border-radius: 0; + background: #f0f0f0; + color: #aaa; + font-weight: 400; + font-family: "Avenir Next", "Helvetica Neue", Helvetica, Arial, sans-serif; + -webkit-appearance: none; /* for box shadows to show on iOS */ +} + +.hbe-input-field:focus { + outline: none; +} + +.hbe-input-label { + display: inline-block; + float: right; + padding: 0 1em; + width: 40%; + color: #696969; + font-weight: bold; + font-size: 70.25%; + -webkit-font-smoothing: antialiased; + -moz-osx-font-smoothing: grayscale; + -webkit-touch-callout: none; + -webkit-user-select: none; + -khtml-user-select: none; + -moz-user-select: none; + -ms-user-select: none; + user-select: none; +} + +.hbe-input-label-content { + position: relative; + display: block; + padding: 1.6em 0; + width: 100%; +} + +.hbe-graphic { + position: absolute; + top: 0; + left: 0; + fill: none; +} + +/* hbe button in post page */ +.hbe-button { + width: 130px; + height: 40px; + background: linear-gradient(to bottom, #4eb5e5 0%,#389ed5 100%); /* W3C */ + border: none; + border-radius: 5px; + position: relative; + border-bottom: 4px solid #2b8bc6; + color: #fbfbfb; + font-weight: 600; + font-family: 'Open Sans', sans-serif; + text-shadow: 1px 1px 1px rgba(0,0,0,.4); + font-size: 15px; + text-align: left; + text-indent: 5px; + box-shadow: 0px 3px 0px 0px rgba(0,0,0,.2); + cursor: pointer; + + display: block; + margin: 0 auto; + margin-bottom: 20px; +} + +.hbe-button:active { + box-shadow: 0px 2px 0px 0px rgba(0,0,0,.2); + top: 1px; +} + +.hbe-button:after { + content: ""; + width: 0; + height: 0; + display: block; + border-top: 20px solid #187dbc; + border-bottom: 20px solid #187dbc; + border-left: 16px solid transparent; + border-right: 20px solid #187dbc; + position: absolute; + opacity: 0.6; + right: 0; + top: 0; + border-radius: 0 5px 5px 0; +} +/* hbe button in post page */ + +/* default theme {{{ */ +.hbe-input-default { + overflow: hidden; +} + +.hbe-input-field-default { + width: 100%; + background: transparent; + padding: 0.5em; + margin-bottom: 2em; + color: #f9f7f6; + z-index: 100; + opacity: 0; +} + +.hbe-input-label-default { + width: 100%; + position: absolute; + text-align: left; + padding: 0.5em 0; + pointer-events: none; + font-size: 1em; +} + +.hbe-input-label-default::before, +.hbe-input-label-default::after { + content: ''; + position: absolute; + width: 100%; + left: 0; +} + +.hbe-input-label-default::before { + height: 100%; + background: #666666; + top: 0; + -webkit-transform: translate3d(0, -100%, 0); + transform: translate3d(0, -100%, 0); + -webkit-transition: -webkit-transform 0.2s; + transition: transform 0.2s; +} + +.hbe-input-label-default::after { + height: 2px; + background: #666666; + top: 100%; + -webkit-transition: opacity 0.2s; + transition: opacity 0.2s; +} + +.hbe-input-label-content-default { + padding: 0; + -webkit-transform-origin: 0 0; + transform-origin: 0 0; + -webkit-transition: -webkit-transform 0.2s, color 0.2s; + transition: transform 0.2s, color 0.2s; +} + +.hbe-input-field-default:focus, +.hbe-input--filled .hbe-input-field-default { + opacity: 1; + -webkit-transition: opacity 0s 0.2s; + transition: opacity 0s 0.2s; +} + +.hbe-input-label-default::before, +.hbe-input-label-default::after, +.hbe-input-label-content-default, +.hbe-input-field-default:focus, +.hbe-input--filled .hbe-input-field-default { + -webkit-transition-timing-function: cubic-bezier(0, 0.25, 0.5, 1); + transition-timing-function: cubic-bezier(0, 0.25, 0.5, 1); +} + +.hbe-input-field-default:focus + .hbe-input-label-default::before, +.hbe-input--filled .hbe-input-label-default::before { + -webkit-transform: translate3d(0, 0, 0); + transform: translate3d(0, 0, 0); +} + +.hbe-input-field-default:focus + .hbe-input-label-default::after, +.hbe-input--filled .hbe-input-label-default::after { + opacity: 0; +} + +.hbe-input-field-default:focus + .hbe-input-label-default .hbe-input-label-content-default, +.hbe-input--filled .hbe-input-label-default .hbe-input-label-content-default { + color: #555555; + -webkit-transform: translate3d(0, 2.1em, 0) scale3d(0.65, 0.65, 1); + transform: translate3d(0, 2.1em, 0) scale3d(0.65, 0.65, 1); +} +/* default theme }}} */ + +/* up theme {{{ */ +.hbe-input-up { + overflow: hidden; + padding-top: 2em; +} + +.hbe-input-field-up { + width: 100%; + background: transparent; + opacity: 0; + padding: 0.35em; + z-index: 100; + color: #837482; +} + +.hbe-input-label-up { + width: 100%; + bottom: 0; + position: absolute; + pointer-events: none; + text-align: left; + color: #8E9191; + padding: 0 0.5em; +} + +.hbe-input-label-up::before { + content: ''; + position: absolute; + width: 100%; + height: 4em; + top: 100%; + left: 0; + background: #fff; + border-top: 4px solid #9B9F9F; + -webkit-transform: translate3d(0, -3px, 0); + transform: translate3d(0, -3px, 0); + -webkit-transition: -webkit-transform 0.4s; + transition: transform 0.4s; + -webkit-transition-timing-function: cubic-bezier(0.7, 0, 0.3, 1); + transition-timing-function: cubic-bezier(0.7, 0, 0.3, 1); +} + +.hbe-input-label-content-up { + padding: 0.5em 0; + -webkit-transform-origin: 0% 100%; + transform-origin: 0% 100%; + -webkit-transition: -webkit-transform 0.4s, color 0.4s; + transition: transform 0.4s, color 0.4s; + -webkit-transition-timing-function: cubic-bezier(0.7, 0, 0.3, 1); + transition-timing-function: cubic-bezier(0.7, 0, 0.3, 1); +} + +.hbe-input-field-up:focus, +.input--filled .hbe-input-field-up { + cursor: text; + opacity: 1; + -webkit-transition: opacity 0s 0.4s; + transition: opacity 0s 0.4s; +} + +.hbe-input-field-up:focus + .hbe-input-label-up::before, +.input--filled .hbe-input-label-up::before { + -webkit-transition-delay: 0.05s; + transition-delay: 0.05s; + -webkit-transform: translate3d(0, -3.3em, 0); + transform: translate3d(0, -3.3em, 0); +} + +.hbe-input-field-up:focus + .hbe-input-label-up .hbe-input-label-content-up, +.input--filled .hbe-input-label-content-up { + color: #6B6E6E; + -webkit-transform: translate3d(0, -3.3em, 0) scale3d(0.81, 0.81, 1); + transform: translate3d(0, -3.3em, 0) scale3d(0.81, 0.81, 1); +} +/* up theme }}} */ + +/* wave theme {{{ */ +.hbe-input-wave { + overflow: hidden; + padding-top: 1em; +} + +.hbe-input-field-wave { + padding: 0.5em 0em 0.25em; + width: 100%; + background: transparent; + color: #9da8b2; + font-size: 1.25em; +} + +.hbe-input-label-wave { + position: absolute; + top: 0.95em; + font-size: 0.85em; + left: 0; + display: block; + width: 100%; + text-align: left; + padding: 0em; + pointer-events: none; + -webkit-transform-origin: 0 0; + transform-origin: 0 0; + -webkit-transition: -webkit-transform 0.2s 0.15s, color 1s; + transition: transform 0.2s 0.15s, color 1s; + -webkit-transition-timing-function: ease-out; + transition-timing-function: ease-out; +} + +.hbe-graphic-wave { + stroke: #92989e; + pointer-events: none; + -webkit-transition: -webkit-transform 0.7s, stroke 0.7s; + transition: transform 0.7s, stroke 0.7s; + -webkit-transition-timing-function: cubic-bezier(0, 0.25, 0.5, 1); + transition-timing-function: cubic-bezier(0, 0.25, 0.5, 1); +} + +.hbe-input-field-wave:focus + .hbe-input-label-wave, +.input--filled .hbe-input-label-wave { + color: #333; + -webkit-transform: translate3d(0, -1.25em, 0) scale3d(0.75, 0.75, 1); + transform: translate3d(0, -1.25em, 0) scale3d(0.75, 0.75, 1); +} + +.hbe-input-field-wave:focus ~ .hbe-graphic-wave, +.input--filled .graphic-wave { + stroke: #333; + -webkit-transform: translate3d(-66.6%, 0, 0); + transform: translate3d(-66.6%, 0, 0); +} +/* wave theme }}} */ + +/* flip theme {{{ */ +.hbe-input-field-flip { + width: 100%; + background-color: #d0d1d0; + border: 2px solid transparent; + -webkit-transition: background-color 0.25s, border-color 0.25s; + transition: background-color 0.25s, border-color 0.25s; +} + +.hbe-input-label-flip { + width: 100%; + text-align: left; + position: absolute; + bottom: 100%; + pointer-events: none; + overflow: hidden; + padding: 0 1.25em; + -webkit-transform: translate3d(0, 3em, 0); + transform: translate3d(0, 3em, 0); + -webkit-transition: -webkit-transform 0.25s; + transition: transform 0.25s ; + -webkit-transition-timing-function: ease-in-out; + transition-timing-function: ease-in-out; +} + +.hbe-input-label-content-flip { + color: #8B8C8B; + padding: 0.25em 0; + -webkit-transition: -webkit-transform 0.25s; + transition: transform 0.25s; + -webkit-transition-timing-function: ease-in-out; + transition-timing-function: ease-in-out; +} + +.hbe-input-label-content-flip::after { + content: attr(data-content); + position: absolute; + font-weight: 800; + bottom: 100%; + left: 0; + height: 100%; + width: 100%; + color: #666666; + padding: 0.25em 0; + letter-spacing: 1px; + font-size: 1em; +} + +.hbe-input-field-flip:focus + .hbe-input-label-flip, +.input--filled .hbe-input-label-flip { + -webkit-transform: translate3d(0, 0, 0); + transform: translate3d(0, 0, 0); +} + +.hbe-input-field-flip:focus + .hbe-input-label-flip .hbe-input-label-content-flip, +.input--filled .hbe-input-label-content-flip { + -webkit-transform: translate3d(0, 100%, 0); + transform: translate3d(0, 100%, 0); +} + +.hbe-input-field-flip:focus + .hbe-input-field-flip, +.input--filled .hbe-input-field-flip { + background-color: transparent; + border-color: #666666; +} +/* flip theme }}} */ + +/* xray theme {{{ */ +.hbe-input-xray { + overflow: hidden; + padding-bottom: 2.5em; +} + +.hbe-input-field-xray { + padding: 0; + margin-top: 1.2em; + width: 100%; + background: transparent; + color: #84AF9B ; + font-size: 1.55em; +} + +.hbe-input-label-xray { + position: absolute; + top: 2em; + left: 0; + display: block; + width: 100%; + text-align: left; + padding: 0em; + letter-spacing: 1px; + color: #84AF9B ; + pointer-events: none; + -webkit-transform-origin: 0 0; + transform-origin: 0 0; + -webkit-transition: -webkit-transform 0.2s 0.1s, color 0.3s; + transition: transform 0.2s 0.1s, color 0.3s; + -webkit-transition-timing-function: ease-out; + transition-timing-function: ease-out; +} + +.hbe-graphic-xray { + stroke: #84AF9B ; + pointer-events: none; + stroke-width: 2px; + top: 1.25em; + bottom: 0px; + height: 3.275em; + -webkit-transition: -webkit-transform 0.7s, stroke 0.7s; + transition: transform 0.7s, stroke 0.7s; + -webkit-transition-timing-function: cubic-bezier(0, 0.25, 0.5, 1); + transition-timing-function: cubic-bezier(0, 0.25, 0.5, 1); +} + +.hbe-input-field-xray:focus + .hbe-input-label-xray, +.input--filled .hbe-input-label-xray { + color: #84AF9B ; + -webkit-transform: translate3d(0, 3.5em, 0) scale3d(0.85, 0.85, 1); + transform: translate3d(0, 3.5em, 0) scale3d(0.85, 0.85, 1); +} + +.hbe-input-field-xray:focus ~ .hbe-graphic-xray, +.input--filled .graphic-xray { + stroke: #84AF9B ; + -webkit-transform: translate3d(-66.6%, 0, 0); + transform: translate3d(-66.6%, 0, 0); +} +/* xray theme }}} */ + +/* blink theme {{{ */ +.hbe-input-blink { + padding-top: 1em; +} + +.hbe-input-field-blink { + width: 100%; + padding: 0.8em 0.5em; + background: transparent; + border: 2px solid; + color: #8781bd; + -webkit-transition: border-color 0.25s; + transition: border-color 0.25s; +} + +.hbe-input-label-blink { + width: 100%; + position: absolute; + top: 0; + text-align: left; + overflow: hidden; + padding: 0; + pointer-events: none; + -webkit-transform: translate3d(0, 3em, 0); + transform: translate3d(0, 3em, 0); +} + +.hbe-input-label-content-blink { + padding: 0 1em; + font-weight: 400; + color: #b5b5b5; +} + +.hbe-input-label-content-blink::after { + content: attr(data-content); + position: absolute; + top: -200%; + left: 0; + color: #8781bd ; + font-weight: 800; +} + +.hbe-input-field-blink:focus, +.input--filled .hbe-input-field-blink { + border-color: #8781bd ; +} + +.hbe-input-field-blink:focus + .hbe-input-label-blink, +.input--filled .hbe-input-label-blink { + -webkit-animation: anim-blink-1 0.25s forwards; + animation: anim-blink-1 0.25s forwards; +} + +.hbe-input-field-blink:focus + .hbe-input-label-blink .hbe-input-label-content-blink, +.input--filled .hbe-input-label-content-blink { + -webkit-animation: anim-blink-2 0.25s forwards ease-in; + animation: anim-blink-2 0.25s forwards ease-in; +} + +@-webkit-keyframes anim-blink-1 { + 0%, 70% { + -webkit-transform: translate3d(0, 3em, 0); + transform: translate3d(0, 3em, 0); + } + 71%, 100% { + -webkit-transform: translate3d(0, 0, 0); + transform: translate3d(0, 0, 0); + } +} + +@-webkit-keyframes anim-blink-2 { + 0% { + -webkit-transform: translate3d(0, 0, 0); + transform: translate3d(0, 0, 0); + } + 70%, 71% { + -webkit-transform: translate3d(0, 125%, 0); + transform: translate3d(0, 125%, 0); + opacity: 0; + -webkit-animation-timing-function: ease-out; + } + 100% { + color: transparent; + -webkit-transform: translate3d(0, 200%, 0); + transform: translate3d(0, 200%, 0); + } +} + +@keyframes anim-blink-1 { + 0%, 70% { + -webkit-transform: translate3d(0, 3em, 0); + transform: translate3d(0, 3em, 0); + } + 71%, 100% { + -webkit-transform: translate3d(0, 0, 0); + transform: translate3d(0, 0, 0); + } +} + +@keyframes anim-blink-2 { + 0% { + -webkit-transform: translate3d(0, 0, 0); + transform: translate3d(0, 0, 0); + } + 70%, 71% { + -webkit-transform: translate3d(0, 125%, 0); + transform: translate3d(0, 125%, 0); + opacity: 0; + -webkit-animation-timing-function: ease-out; + } + 100% { + color: transparent; + -webkit-transform: translate3d(0, 200%, 0); + transform: translate3d(0, 200%, 0); + } +} +/* blink theme }}} */ + +/* surge theme {{{ */ +.hbe-input-surge { + overflow: hidden; + padding-bottom: 1em; +} + +.hbe-input-field-surge { + padding: 0.25em 0.5em; + margin-top: 1.25em; + width: 100%; + background: transparent; + color: #D0D0D0; + font-size: 1.55em; + opacity: 0; +} + +.hbe-input-label-surge { + width: 100%; + text-align: left; + position: absolute; + top: 1em; + pointer-events: none; + overflow: hidden; + padding: 0 0.25em; + -webkit-transform: translate3d(1em, 2.75em, 0); + transform: translate3d(1em, 2.75em, 0); + -webkit-transition: -webkit-transform 0.3s; + transition: transform 0.3s; +} + +.hbe-input-label-content-surge { + color: #A4A5A6; + padding: 0.4em 0 0.25em; + -webkit-transition: -webkit-transform 0.3s; + transition: transform 0.3s; +} + +.hbe-input-label-content-surge::after { + content: attr(data-content); + position: absolute; + font-weight: 800; + top: 100%; + left: 0; + height: 100%; + width: 100%; + color: #2C3E50; + padding: 0.25em 0; + letter-spacing: 1px; + font-size: 0.85em; +} + +.hbe-graphic-surge { + fill: #2C3E50; + pointer-events: none; + top: 1em; + bottom: 0px; + height: 4.5em; + z-index: -1; + -webkit-transition: -webkit-transform 0.7s, fill 0.7s; + transition: transform 0.7s, fill 0.7s; + -webkit-transition-timing-function: cubic-bezier(0, 0.25, 0.5, 1); + transition-timing-function: cubic-bezier(0, 0.25, 0.5, 1); +} + +.hbe-input-field-surge:focus, +.input--filled .hbe-input-field-surge { + -webkit-transition: opacity 0s 0.35s; + transition: opacity 0s 0.35s; + opacity: 1; +} + +.hbe-input-field-surge:focus + .hbe-input-label-surge, +.input--filled .hbe-input-label-surge { + -webkit-transition-delay: 0.15s; + transition-delay: 0.15s; + -webkit-transform: translate3d(0, 0, 0); + transform: translate3d(0, 0, 0); +} + +.hbe-input-field-surge:focus + .hbe-input-label-surge .hbe-input-label-content-surge, +.input--filled .hbe-input-label-content-surge { + -webkit-transition-delay: 0.15s; + transition-delay: 0.15s; + -webkit-transform: translate3d(0, -100%, 0); + transform: translate3d(0, -100%, 0); +} + +.hbe-input-field-surge:focus ~ .hbe-graphic-surge, +.input--filled .graphic-surge { + fill: #2C3E50; + -webkit-transform: translate3d(-66.6%, 0, 0); + transform: translate3d(-66.6%, 0, 0); +} +/* surge theme }}} */ + +/* shrink theme {{{ */ +.hbe-input-field-shrink { + width: 100%; + background: transparent; + padding: 0.5em 0; + margin-bottom: 2em; + color: #2C3E50; +} + +.hbe-input-label-shrink { + width: 100%; + position: absolute; + text-align: left; + font-size: 1em; + padding: 10px 0 5px; + pointer-events: none; +} + +.hbe-input-label-shrink::after { + content: ''; + position: absolute; + width: 100%; + height: 7px; + background: #B7C3AC; + left: 0; + top: 100%; + -webkit-transform-origin: 50% 100%; + transform-origin: 50% 100%; + -webkit-transition: -webkit-transform 0.3s, background-color 0.3s; + transition: transform 0.3s, background-color 0.3s; +} + +.hbe-input-label-content-shrink { + padding: 0; + -webkit-transform-origin: 0 0; + transform-origin: 0 0; + -webkit-transition: -webkit-transform 0.3s, color 0.3s; + transition: transform 0.3s, color 0.3s; +} + +.hbe-input-field-shrink:focus + .hbe-input-label-shrink::after, +.input--filled .hbe-input-label-shrink::after { + background: #84AF9B; + -webkit-transform: scale3d(1, 0.25, 1); + transform: scale3d(1, 0.25, 1); +} + +.hbe-input-field-shrink:focus + .hbe-input-label-shrink .hbe-input-label-content-shrink, +.input--filled .hbe-input-label-shrink .hbe-input-label-content-shrink { + color: #84AF9B; + -webkit-transform: translate3d(0, 2em, 0) scale3d(0.655, 0.655, 1); + transform: translate3d(0, 2em, 0) scale3d(0.655, 0.655, 1); +} +/* shrink theme }}} */ diff --git a/css/index.css b/css/index.css new file mode 100644 index 0000000..be1f28a --- /dev/null +++ b/css/index.css @@ -0,0 +1,6372 @@ +/*! normalize.css v8.0.1 | MIT License | github.com/necolas/normalize.css */ +html { + line-height: 1.15; + -webkit-text-size-adjust: 100% +} + +body { + margin: 0 +} + +main { + display: block +} + +h1 { + font-size: 2em; + margin: .67em 0 +} + +hr { + box-sizing: content-box; + height: 0; + overflow: visible +} + +pre { + font-family: monospace, monospace; + font-size: 1em +} + +a { + background-color: transparent +} + +abbr[title] { + border-bottom: none; + text-decoration: underline; + text-decoration: underline dotted +} + +b, +strong { + font-weight: bolder +} + +code, +kbd, +samp { + font-family: monospace, monospace; + font-size: 1em +} + +small { + font-size: 80% +} + +sub, +sup { + font-size: 75%; + line-height: 0; + position: relative; + vertical-align: baseline +} + +sub { + bottom: -.25em +} + +sup { + top: -.5em +} + +img { + border-style: none +} + +button, +input, +optgroup, +select, +textarea { + font-family: inherit; + font-size: 100%; + line-height: 1.15; + margin: 0 +} + +button, +input { + overflow: visible +} + +button, +select { + text-transform: none +} + +[type=button], +[type=reset], +[type=submit], +button { + -webkit-appearance: button +} + +[type=button]::-moz-focus-inner, +[type=reset]::-moz-focus-inner, +[type=submit]::-moz-focus-inner, +button::-moz-focus-inner { + border-style: none; + padding: 0 +} + +[type=button]:-moz-focusring, +[type=reset]:-moz-focusring, +[type=submit]:-moz-focusring, +button:-moz-focusring { + outline: 1px dotted ButtonText +} + +fieldset { + padding: .35em .75em .625em +} + +legend { + box-sizing: border-box; + color: inherit; + display: table; + max-width: 100%; + padding: 0; + white-space: normal +} + +progress { + vertical-align: baseline +} + +textarea { + overflow: auto +} + +[type=checkbox], +[type=radio] { + box-sizing: border-box; + padding: 0 +} + +[type=number]::-webkit-inner-spin-button, +[type=number]::-webkit-outer-spin-button { + height: auto +} + +[type=search] { + -webkit-appearance: textfield; + outline-offset: -2px +} + +[type=search]::-webkit-search-decoration { + -webkit-appearance: none +} + +::-webkit-file-upload-button { + -webkit-appearance: button; + font: inherit +} + +details { + display: block +} + +summary { + display: list-item +} + +template { + display: none +} + +[hidden] { + display: none +} +.limit-one-line, +.container .flink .flink-item-name, +.container .flink .flink-item-desc, +#aside-content .card-archives ul.card-archive-list > .card-archive-list-item a span, +#aside-content .card-categories ul.card-category-list > .card-category-list-item a span, +.site-data > a .headline, +#nav #blog-info, +#sidebar #sidebar-menus .menus_items .site-page { + overflow: hidden; + -o-text-overflow: ellipsis; + text-overflow: ellipsis; + white-space: nowrap; +} +.limit-more-line, +.article-sort-item-title, +#recent-posts .recent-post-item >.recent-post-info > .article-title, +#recent-posts .recent-post-item >.recent-post-info > .content, +#aside-content .aside-list > .aside-list-item .content > .name, +#aside-content .aside-list > .aside-list-item .content > .title, +#aside-content .aside-list > .aside-list-item .content > .comment, +#post-info .post-title, +.pagination-related .info .info-1 .info-item-2, +.pagination-related .info .info-2 .info-item-1, +.container figure.gallery-group p, +.container figure.gallery-group .gallery-group-name { + display: -webkit-box; + overflow: hidden; + -webkit-box-orient: vertical; +} +.fontawesomeIcon, +.custom-hr:before, +.container h1:before, +.container h2:before, +.container h3:before, +.container h4:before, +.container h5:before, +.container h6:before, +.container hr:before, +#post .post-copyright:before, +#post #post-outdate-notice:before, +.note:not(.no-icon)::before, +.search-dialog hr:before { + display: inline-block; + font-weight: 600; + font-family: 'Font Awesome 6 Free'; + text-rendering: auto; + -webkit-font-smoothing: antialiased; +} +.cardHover, +.layout > div:first-child:not(.nc), +#recent-posts .recent-post-item, +#article-container .shuoshuo-item, +#aside-content .card-widget, +.layout .pagination > *:not(.space) { + background: var(--card-bg); + -webkit-box-shadow: var(--card-box-shadow); + box-shadow: var(--card-box-shadow); + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; + border-radius: 8px; +} +.cardHover:hover, +.layout > div:first-child:not(.nc):hover, +#recent-posts .recent-post-item:hover, +#article-container .shuoshuo-item:hover, +#aside-content .card-widget:hover, +.layout .pagination > *:not(.space):hover { + -webkit-box-shadow: var(--card-hover-box-shadow); + box-shadow: var(--card-hover-box-shadow); +} +.imgHover, +.article-sort-item-img :first-child, +#recent-posts .recent-post-item .post_cover .post-bg, +#aside-content .aside-list > .aside-list-item .thumbnail :first-child { + width: 100%; + height: 100%; + -webkit-transition: filter 375ms ease-in 0.2s, -webkit-transform 0.6s; + -moz-transition: filter 375ms ease-in 0.2s, -moz-transform 0.6s; + -o-transition: filter 375ms ease-in 0.2s, -o-transform 0.6s; + -ms-transition: filter 375ms ease-in 0.2s, -ms-transform 0.6s; + transition: filter 375ms ease-in 0.2s, transform 0.6s; + object-fit: cover; +} +.imgHover:hover, +.article-sort-item-img :first-child:hover, +#recent-posts .recent-post-item .post_cover .post-bg:hover, +#aside-content .aside-list > .aside-list-item .thumbnail :first-child:hover { + -webkit-transform: scale(1.1); + -moz-transform: scale(1.1); + -o-transform: scale(1.1); + -ms-transform: scale(1.1); + transform: scale(1.1); +} +.postImgHover:hover .cover, +.pagination-related:hover .cover { + opacity: 0.5; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=50)"; + filter: alpha(opacity=50); + -webkit-transform: scale(1.1); + -moz-transform: scale(1.1); + -o-transform: scale(1.1); + -ms-transform: scale(1.1); + transform: scale(1.1); +} +.postImgHover .cover, +.pagination-related .cover { + width: 100%; + height: 100%; + opacity: 0.4; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=40)"; + filter: alpha(opacity=40); + -webkit-transition: all 0.6s, filter 375ms ease-in 0.2s; + -moz-transition: all 0.6s, filter 375ms ease-in 0.2s; + -o-transition: all 0.6s, filter 375ms ease-in 0.2s; + -ms-transition: all 0.6s, filter 375ms ease-in 0.2s; + transition: all 0.6s, filter 375ms ease-in 0.2s; + object-fit: cover; +} +.list-beauty, +.category-lists ul { + list-style: none; +} +.list-beauty li, +.category-lists ul li { + position: relative; + padding: 0.12em 0.4em 0.12em 1.4em; +} +.list-beauty li:hover:before, +.category-lists ul li:hover:before { + border-color: var(--pseudo-hover); +} +.list-beauty li:before, +.category-lists ul li:before { + position: absolute; + top: 0.67em; + left: 0; + width: 0.43em; + height: 0.43em; + border: 0.215em solid #49b1f5; + border-radius: 0.43em; + background: transparent; + content: ''; + cursor: pointer; + -webkit-transition: all 0.3s ease-out; + -moz-transition: all 0.3s ease-out; + -o-transition: all 0.3s ease-out; + -ms-transition: all 0.3s ease-out; + transition: all 0.3s ease-out; +} +.custom-hr, +.container hr, +.search-dialog hr { + position: relative; + margin: 40px auto; + border: 2px dashed var(--hr-border); + width: calc(100% - 4px); +} +.custom-hr:hover:before, +.container hr:hover:before, +.search-dialog hr:hover:before { + left: calc(95% - 20px); +} +.custom-hr:before, +.container hr:before, +.search-dialog hr:before { + position: absolute; + top: -10px; + left: 5%; + z-index: 1; + color: var(--hr-before-color); + content: '\f0c4'; + font-size: 20px; + line-height: 1; + -webkit-transition: all 1s ease-in-out; + -moz-transition: all 1s ease-in-out; + -o-transition: all 1s ease-in-out; + -ms-transition: all 1s ease-in-out; + transition: all 1s ease-in-out; +} +.verticalCenter, +.pagination-related .info .info-1, +.pagination-related .info .info-2 { + position: absolute; + top: 50%; + width: 100%; + -webkit-transform: translate(0, -50%); + -moz-transform: translate(0, -50%); + -o-transform: translate(0, -50%); + -ms-transform: translate(0, -50%); + transform: translate(0, -50%); +} +#content-inner, +#footer { + -webkit-animation: bottom-top 1s; + -moz-animation: bottom-top 1s; + -o-animation: bottom-top 1s; + -ms-animation: bottom-top 1s; + animation: bottom-top 1s; +} +#page-header:not(.full_page), +#nav.show { + -webkit-animation: header-effect 1s; + -moz-animation: header-effect 1s; + -o-animation: header-effect 1s; + -ms-animation: header-effect 1s; + animation: header-effect 1s; +} +#site-title, +#site-subtitle { + -webkit-animation: titleScale 1s; + -moz-animation: titleScale 1s; + -o-animation: titleScale 1s; + -ms-animation: titleScale 1s; + animation: titleScale 1s; +} +canvas:not(#ribbon-canvas), +#web_bg { + -webkit-animation: to_show 4s; + -moz-animation: to_show 4s; + -o-animation: to_show 4s; + -ms-animation: to_show 4s; + animation: to_show 4s; +} +#ribbon-canvas { + -webkit-animation: ribbon_to_show 4s; + -moz-animation: ribbon_to_show 4s; + -o-animation: ribbon_to_show 4s; + -ms-animation: ribbon_to_show 4s; + animation: ribbon_to_show 4s; +} +#sidebar-menus.open > :nth-child(1) { + -webkit-animation: sidebarItem 0.2s; + -moz-animation: sidebarItem 0.2s; + -o-animation: sidebarItem 0.2s; + -ms-animation: sidebarItem 0.2s; + animation: sidebarItem 0.2s; +} +#sidebar-menus.open > :nth-child(2) { + -webkit-animation: sidebarItem 0.4s; + -moz-animation: sidebarItem 0.4s; + -o-animation: sidebarItem 0.4s; + -ms-animation: sidebarItem 0.4s; + animation: sidebarItem 0.4s; +} +#sidebar-menus.open > :nth-child(3) { + -webkit-animation: sidebarItem 0.6s; + -moz-animation: sidebarItem 0.6s; + -o-animation: sidebarItem 0.6s; + -ms-animation: sidebarItem 0.6s; + animation: sidebarItem 0.6s; +} +#sidebar-menus.open > :nth-child(4) { + -webkit-animation: sidebarItem 0.8s; + -moz-animation: sidebarItem 0.8s; + -o-animation: sidebarItem 0.8s; + -ms-animation: sidebarItem 0.8s; + animation: sidebarItem 0.8s; +} +.scroll-down-effects { + -webkit-animation: scroll-down-effect 1.5s infinite; + -moz-animation: scroll-down-effect 1.5s infinite; + -o-animation: scroll-down-effect 1.5s infinite; + -ms-animation: scroll-down-effect 1.5s infinite; + animation: scroll-down-effect 1.5s infinite; +} +.reward-main { + -webkit-animation: donate_effcet 0.3s 0.1s ease both; + -moz-animation: donate_effcet 0.3s 0.1s ease both; + -o-animation: donate_effcet 0.3s 0.1s ease both; + -ms-animation: donate_effcet 0.3s 0.1s ease both; + animation: donate_effcet 0.3s 0.1s ease both; +} +@-moz-keyframes scroll-down-effect { + 0% { + opacity: 0.4; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=40)"; + filter: alpha(opacity=40); + -webkit-transform: translate(0, 0); + -moz-transform: translate(0, 0); + -o-transform: translate(0, 0); + -ms-transform: translate(0, 0); + transform: translate(0, 0); + } + 50% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translate(0, -16px); + -moz-transform: translate(0, -16px); + -o-transform: translate(0, -16px); + -ms-transform: translate(0, -16px); + transform: translate(0, -16px); + } + 100% { + opacity: 0.4; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=40)"; + filter: alpha(opacity=40); + -webkit-transform: translate(0, 0); + -moz-transform: translate(0, 0); + -o-transform: translate(0, 0); + -ms-transform: translate(0, 0); + transform: translate(0, 0); + } +} +@-webkit-keyframes scroll-down-effect { + 0% { + opacity: 0.4; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=40)"; + filter: alpha(opacity=40); + -webkit-transform: translate(0, 0); + -moz-transform: translate(0, 0); + -o-transform: translate(0, 0); + -ms-transform: translate(0, 0); + transform: translate(0, 0); + } + 50% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translate(0, -16px); + -moz-transform: translate(0, -16px); + -o-transform: translate(0, -16px); + -ms-transform: translate(0, -16px); + transform: translate(0, -16px); + } + 100% { + opacity: 0.4; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=40)"; + filter: alpha(opacity=40); + -webkit-transform: translate(0, 0); + -moz-transform: translate(0, 0); + -o-transform: translate(0, 0); + -ms-transform: translate(0, 0); + transform: translate(0, 0); + } +} +@-o-keyframes scroll-down-effect { + 0% { + opacity: 0.4; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=40)"; + filter: alpha(opacity=40); + -webkit-transform: translate(0, 0); + -moz-transform: translate(0, 0); + -o-transform: translate(0, 0); + -ms-transform: translate(0, 0); + transform: translate(0, 0); + } + 50% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translate(0, -16px); + -moz-transform: translate(0, -16px); + -o-transform: translate(0, -16px); + -ms-transform: translate(0, -16px); + transform: translate(0, -16px); + } + 100% { + opacity: 0.4; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=40)"; + filter: alpha(opacity=40); + -webkit-transform: translate(0, 0); + -moz-transform: translate(0, 0); + -o-transform: translate(0, 0); + -ms-transform: translate(0, 0); + transform: translate(0, 0); + } +} +@keyframes scroll-down-effect { + 0% { + opacity: 0.4; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=40)"; + filter: alpha(opacity=40); + -webkit-transform: translate(0, 0); + -moz-transform: translate(0, 0); + -o-transform: translate(0, 0); + -ms-transform: translate(0, 0); + transform: translate(0, 0); + } + 50% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translate(0, -16px); + -moz-transform: translate(0, -16px); + -o-transform: translate(0, -16px); + -ms-transform: translate(0, -16px); + transform: translate(0, -16px); + } + 100% { + opacity: 0.4; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=40)"; + filter: alpha(opacity=40); + -webkit-transform: translate(0, 0); + -moz-transform: translate(0, 0); + -o-transform: translate(0, 0); + -ms-transform: translate(0, 0); + transform: translate(0, 0); + } +} +@-moz-keyframes header-effect { + 0% { + -webkit-transform: translateY(-35px); + -moz-transform: translateY(-35px); + -o-transform: translateY(-35px); + -ms-transform: translateY(-35px); + transform: translateY(-35px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-webkit-keyframes header-effect { + 0% { + -webkit-transform: translateY(-35px); + -moz-transform: translateY(-35px); + -o-transform: translateY(-35px); + -ms-transform: translateY(-35px); + transform: translateY(-35px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-o-keyframes header-effect { + 0% { + -webkit-transform: translateY(-35px); + -moz-transform: translateY(-35px); + -o-transform: translateY(-35px); + -ms-transform: translateY(-35px); + transform: translateY(-35px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@keyframes header-effect { + 0% { + -webkit-transform: translateY(-35px); + -moz-transform: translateY(-35px); + -o-transform: translateY(-35px); + -ms-transform: translateY(-35px); + transform: translateY(-35px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-moz-keyframes bottom-top { + 0% { + -webkit-transform: translateY(35px); + -moz-transform: translateY(35px); + -o-transform: translateY(35px); + -ms-transform: translateY(35px); + transform: translateY(35px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-webkit-keyframes bottom-top { + 0% { + -webkit-transform: translateY(35px); + -moz-transform: translateY(35px); + -o-transform: translateY(35px); + -ms-transform: translateY(35px); + transform: translateY(35px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-o-keyframes bottom-top { + 0% { + -webkit-transform: translateY(35px); + -moz-transform: translateY(35px); + -o-transform: translateY(35px); + -ms-transform: translateY(35px); + transform: translateY(35px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@keyframes bottom-top { + 0% { + -webkit-transform: translateY(35px); + -moz-transform: translateY(35px); + -o-transform: translateY(35px); + -ms-transform: translateY(35px); + transform: translateY(35px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-moz-keyframes titleScale { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } +} +@-webkit-keyframes titleScale { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } +} +@-o-keyframes titleScale { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } +} +@keyframes titleScale { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } +} +@-moz-keyframes search_close { + 0% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } + 100% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } +} +@-webkit-keyframes search_close { + 0% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } + 100% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } +} +@-o-keyframes search_close { + 0% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } + 100% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } +} +@keyframes search_close { + 0% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } + 100% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } +} +@-moz-keyframes to_show { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + } +} +@-webkit-keyframes to_show { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + } +} +@-o-keyframes to_show { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + } +} +@keyframes to_show { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + } +} +@-moz-keyframes to_hide { + 0% { + opacity: 1; + -ms-filter: none; + filter: none; + } + 100% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } +} +@-webkit-keyframes to_hide { + 0% { + opacity: 1; + -ms-filter: none; + filter: none; + } + 100% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } +} +@-o-keyframes to_hide { + 0% { + opacity: 1; + -ms-filter: none; + filter: none; + } + 100% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } +} +@keyframes to_hide { + 0% { + opacity: 1; + -ms-filter: none; + filter: none; + } + 100% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } +} +@-moz-keyframes ribbon_to_show { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } + 100% { + opacity: 0.6; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=60)"; + filter: alpha(opacity=60); + } +} +@-webkit-keyframes ribbon_to_show { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } + 100% { + opacity: 0.6; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=60)"; + filter: alpha(opacity=60); + } +} +@-o-keyframes ribbon_to_show { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } + 100% { + opacity: 0.6; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=60)"; + filter: alpha(opacity=60); + } +} +@keyframes ribbon_to_show { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + } + 100% { + opacity: 0.6; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=60)"; + filter: alpha(opacity=60); + } +} +@-moz-keyframes avatar_turn_around { + from { + -webkit-transform: rotate(0); + -moz-transform: rotate(0); + -o-transform: rotate(0); + -ms-transform: rotate(0); + transform: rotate(0); + } + to { + -webkit-transform: rotate(360deg); + -moz-transform: rotate(360deg); + -o-transform: rotate(360deg); + -ms-transform: rotate(360deg); + transform: rotate(360deg); + } +} +@-webkit-keyframes avatar_turn_around { + from { + -webkit-transform: rotate(0); + -moz-transform: rotate(0); + -o-transform: rotate(0); + -ms-transform: rotate(0); + transform: rotate(0); + } + to { + -webkit-transform: rotate(360deg); + -moz-transform: rotate(360deg); + -o-transform: rotate(360deg); + -ms-transform: rotate(360deg); + transform: rotate(360deg); + } +} +@-o-keyframes avatar_turn_around { + from { + -webkit-transform: rotate(0); + -moz-transform: rotate(0); + -o-transform: rotate(0); + -ms-transform: rotate(0); + transform: rotate(0); + } + to { + -webkit-transform: rotate(360deg); + -moz-transform: rotate(360deg); + -o-transform: rotate(360deg); + -ms-transform: rotate(360deg); + transform: rotate(360deg); + } +} +@keyframes avatar_turn_around { + from { + -webkit-transform: rotate(0); + -moz-transform: rotate(0); + -o-transform: rotate(0); + -ms-transform: rotate(0); + transform: rotate(0); + } + to { + -webkit-transform: rotate(360deg); + -moz-transform: rotate(360deg); + -o-transform: rotate(360deg); + -ms-transform: rotate(360deg); + transform: rotate(360deg); + } +} +@-moz-keyframes sub_menus { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: translateY(10px); + -moz-transform: translateY(10px); + -o-transform: translateY(10px); + -ms-transform: translateY(10px); + transform: translateY(10px); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-webkit-keyframes sub_menus { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: translateY(10px); + -moz-transform: translateY(10px); + -o-transform: translateY(10px); + -ms-transform: translateY(10px); + transform: translateY(10px); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-o-keyframes sub_menus { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: translateY(10px); + -moz-transform: translateY(10px); + -o-transform: translateY(10px); + -ms-transform: translateY(10px); + transform: translateY(10px); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@keyframes sub_menus { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: translateY(10px); + -moz-transform: translateY(10px); + -o-transform: translateY(10px); + -ms-transform: translateY(10px); + transform: translateY(10px); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-moz-keyframes donate_effcet { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: translateY(-20px); + -moz-transform: translateY(-20px); + -o-transform: translateY(-20px); + -ms-transform: translateY(-20px); + transform: translateY(-20px); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-webkit-keyframes donate_effcet { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: translateY(-20px); + -moz-transform: translateY(-20px); + -o-transform: translateY(-20px); + -ms-transform: translateY(-20px); + transform: translateY(-20px); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-o-keyframes donate_effcet { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: translateY(-20px); + -moz-transform: translateY(-20px); + -o-transform: translateY(-20px); + -ms-transform: translateY(-20px); + transform: translateY(-20px); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@keyframes donate_effcet { + 0% { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: translateY(-20px); + -moz-transform: translateY(-20px); + -o-transform: translateY(-20px); + -ms-transform: translateY(-20px); + transform: translateY(-20px); + } + 100% { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-moz-keyframes sidebarItem { + 0% { + -webkit-transform: translateX(200px); + -moz-transform: translateX(200px); + -o-transform: translateX(200px); + -ms-transform: translateX(200px); + transform: translateX(200px); + } + 100% { + -webkit-transform: translateX(0); + -moz-transform: translateX(0); + -o-transform: translateX(0); + -ms-transform: translateX(0); + transform: translateX(0); + } +} +@-webkit-keyframes sidebarItem { + 0% { + -webkit-transform: translateX(200px); + -moz-transform: translateX(200px); + -o-transform: translateX(200px); + -ms-transform: translateX(200px); + transform: translateX(200px); + } + 100% { + -webkit-transform: translateX(0); + -moz-transform: translateX(0); + -o-transform: translateX(0); + -ms-transform: translateX(0); + transform: translateX(0); + } +} +@-o-keyframes sidebarItem { + 0% { + -webkit-transform: translateX(200px); + -moz-transform: translateX(200px); + -o-transform: translateX(200px); + -ms-transform: translateX(200px); + transform: translateX(200px); + } + 100% { + -webkit-transform: translateX(0); + -moz-transform: translateX(0); + -o-transform: translateX(0); + -ms-transform: translateX(0); + transform: translateX(0); + } +} +@keyframes sidebarItem { + 0% { + -webkit-transform: translateX(200px); + -moz-transform: translateX(200px); + -o-transform: translateX(200px); + -ms-transform: translateX(200px); + transform: translateX(200px); + } + 100% { + -webkit-transform: translateX(0); + -moz-transform: translateX(0); + -o-transform: translateX(0); + -ms-transform: translateX(0); + transform: translateX(0); + } +} +:root { + --global-font-size: 18px; + --global-bg: #fff; + --font-color: #4c4948; + --hr-border: #a4d8fa; + --hr-before-color: #80c8f8; + --search-bg: #f6f8fa; + --search-input-color: #4c4948; + --search-a-color: #4c4948; + --preloader-bg: #37474f; + --preloader-color: #fff; + --tab-border-color: #f0f0f0; + --tab-botton-bg: #f0f0f0; + --tab-botton-color: #1f2d3d; + --tab-button-hover-bg: #dcdcdc; + --tab-button-active-bg: #fff; + --card-bg: #fff; + --card-meta: #858585; + --sidebar-bg: #f6f8fa; + --sidebar-menu-bg: #fff; + --btn-hover-color: #ff7242; + --btn-color: #fff; + --btn-bg: #49b1f5; + --text-bg-hover: rgba(73,177,245,0.7); + --light-grey: #eee; + --dark-grey: #cacaca; + --white: #fff; + --text-highlight-color: #1f2d3d; + --blockquote-color: #6a737d; + --blockquote-bg: rgba(73,177,245,0.1); + --reward-pop: #f5f5f5; + --toc-link-color: #666261; + --card-box-shadow: 0 3px 8px 6px rgba(7,17,27,0.05); + --card-hover-box-shadow: 0 3px 8px 6px rgba(7,17,27,0.09); + --pseudo-hover: #ff7242; + --headline-presudo: #a0a0a0; + --scrollbar-color: #49b1f5; + --default-bg-color: #49b1f5; + --zoom-bg: #fff; + --mark-bg: rgba(0,0,0,0.3); +} +body { + position: relative; + overflow-y: scroll; + min-height: 100%; + background: var(--global-bg); + color: var(--font-color); + font-size: var(--global-font-size); + font-family: -apple-system, BlinkMacSystemFont, 'Segoe UI', 'Helvetica Neue', Lato, Roboto, 'PingFang SC', 'Microsoft JhengHei', sans-serif; + line-height: 2; + -webkit-tap-highlight-color: rgba(0,0,0,0); + scroll-behavior: smooth; +} +@-moz-document url-prefix() { + * { + scrollbar-width: thin; + scrollbar-color: var(--scrollbar-color) transparent; + } +} +*::-webkit-scrollbar { + width: 5px; + height: 5px; +} +*::-webkit-scrollbar-thumb { + background: var(--scrollbar-color); +} +*::-webkit-scrollbar-track { + background-color: transparent; +} +input::placeholder { + color: var(--font-color); +} +#web_bg { + position: fixed; + z-index: -999; + width: 100%; + height: 100%; + background-attachment: local; + background-position: center; + background-size: cover; + background-repeat: no-repeat; +} +h1, +h2, +h3, +h4, +h5, +h6 { + position: relative; + margin: 20px 0 14px; + color: var(--text-highlight-color); + font-weight: bold; +} +h1 code, +h2 code, +h3 code, +h4 code, +h5 code, +h6 code { + font-size: inherit !important; +} +* { + -webkit-box-sizing: border-box; + -moz-box-sizing: border-box; + box-sizing: border-box; +} +.table-wrap { + overflow-x: scroll; + margin: 0 0 20px; + border-radius: 5px; +} +.table-wrap table { + border-radius: 5px; +} +.table-wrap table thead > tr:first-child th:first-child { + border-top-left-radius: 5px; +} +.table-wrap table thead > tr:first-child th:last-child { + border-top-right-radius: 5px; +} +.table-wrap table tbody > tr:last-child td:first-child { + border-bottom-left-radius: 5px; +} +.table-wrap table tbody > tr:last-child td:last-child { + border-bottom-right-radius: 5px; +} +table { + display: table; + width: 100%; + border-spacing: 0; + border-collapse: separate; + border-top: 1px solid var(--light-grey); + border-left: 1px solid var(--light-grey); + empty-cells: show; +} +table thead { + background: rgba(153,169,191,0.1); +} +table th, +table td { + padding: 6px 12px; + border: 1px solid var(--light-grey); + border-top: none; + border-left: none; + vertical-align: middle; +} +*::selection { + background: #00c4b6; + color: #f7f7f7; +} +button { + padding: 0; + outline: 0; + border: none; + background: none; + cursor: pointer; + touch-action: manipulation; +} +a { + color: #99a9bf; + text-decoration: none; + word-wrap: break-word; + -webkit-transition: all 0.2s; + -moz-transition: all 0.2s; + -o-transition: all 0.2s; + -ms-transition: all 0.2s; + transition: all 0.2s; + overflow-wrap: break-word; +} +a:hover { + color: #49b1f5; +} +.text-center { + text-align: center; +} +.text-right { + text-align: right; +} +img[src=''], +img:not([src]) { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); +} +.img-alt { + margin: -10px 0 10px; + color: #858585; +} +.img-alt:hover { + text-decoration: none !important; +} +blockquote { + margin: 0 0 20px; + padding: 7px 15px; + border-left: 4px solid #49b1f5; + background-color: var(--blockquote-bg); + color: var(--blockquote-color); + border-radius: 6px; +} +blockquote footer cite:before { + padding: 0 5px; + content: '—'; +} +blockquote > :last-child { + margin-bottom: 0 !important; +} +:root { + --hl-color: #eff; + --hl-bg: #212121; + --hltools-bg: #1c1c1c; + --hltools-color: rgba(238,255,255,0.8); + --hlnumber-bg: #212121; + --hlnumber-color: rgba(238,255,255,0.5); + --hlscrollbar-bg: #353535; + --hlexpand-bg: linear-gradient(180deg, rgba(33,33,33,0.6), rgba(33,33,33,0.9)); +} +[data-theme='dark'] { + --hl-color: rgba(255,255,255,0.7); + --hl-bg: #171717; + --hltools-bg: #1a1a1a; + --hltools-color: #90a4ae; + --hlnumber-bg: #171717; + --hlnumber-color: rgba(255,255,255,0.4); + --hlscrollbar-bg: #1f1f1f; + --hlexpand-bg: linear-gradient(180deg, rgba(23,23,23,0.6), rgba(23,23,23,0.9)); +} +@-moz-document url-prefix() { + scrollbar-color: var(--hlscrollbar-bg) transparent; +} +figure.highlight table::-webkit-scrollbar-thumb { + background: var(--hlscrollbar-bg); +} +figure.highlight pre .deletion { + color: #bf42bf; +} +figure.highlight pre .addition { + color: #105ede; +} +figure.highlight pre .meta { + color: #c792ea; +} +figure.highlight pre .comment { + color: #969896; +} +figure.highlight pre .variable, +figure.highlight pre .attribute, +figure.highlight pre .regexp, +figure.highlight pre .ruby .constant, +figure.highlight pre .xml .tag .title, +figure.highlight pre .xml .pi, +figure.highlight pre .xml .doctype, +figure.highlight pre .html .doctype, +figure.highlight pre .css .id, +figure.highlight pre .tag .name, +figure.highlight pre .css .class, +figure.highlight pre .css .pseudo { + color: #ff5370; +} +figure.highlight pre .tag { + color: #89ddff; +} +figure.highlight pre .number, +figure.highlight pre .preprocessor, +figure.highlight pre .literal, +figure.highlight pre .params, +figure.highlight pre .constant, +figure.highlight pre .command { + color: #f78c6c; +} +figure.highlight pre .built_in { + color: #ffcb6b; +} +figure.highlight pre .ruby .class .title, +figure.highlight pre .css .rules .attribute, +figure.highlight pre .string, +figure.highlight pre .value, +figure.highlight pre .inheritance, +figure.highlight pre .header, +figure.highlight pre .ruby .symbol, +figure.highlight pre .xml .cdata, +figure.highlight pre .special, +figure.highlight pre .number, +figure.highlight pre .formula { + color: #c3e88d; +} +figure.highlight pre .keyword, +figure.highlight pre .title, +figure.highlight pre .css .hexcolor { + color: #89ddff; +} +figure.highlight pre .function, +figure.highlight pre .python .decorator, +figure.highlight pre .python .title, +figure.highlight pre .ruby .function .title, +figure.highlight pre .ruby .title .keyword, +figure.highlight pre .perl .sub, +figure.highlight pre .javascript .title, +figure.highlight pre .coffeescript .title { + color: #82aaff; +} +figure.highlight pre .tag .attr, +figure.highlight pre .javascript .function { + color: #c792ea; +} +.container figure.highlight .line.marked { + background-color: rgba(97,97,97,0.314); +} +.container figure.highlight table { + display: block; + overflow: auto; + border: none; +} +.container figure.highlight table td { + padding: 0; + border: none; +} +.container figure.highlight .gutter pre { + padding-right: 10px; + padding-left: 10px; + background-color: var(--hlnumber-bg); + color: var(--hlnumber-color); + text-align: right; +} +.container figure.highlight .code pre { + padding-right: 10px; + padding-left: 10px; + width: 100%; +} +.container pre, +.container figure.highlight { + overflow: auto; + margin: 0 0 20px; + padding: 0; + background: var(--hl-bg); + color: var(--hl-color); + line-height: 1.6; +} +.container pre, +.container code { + font-size: var(--global-font-size); + font-family: consolas, Menlo, 'PingFang SC', 'Microsoft JhengHei', sans-serif !important; + border-radius: 6px; +} +.container code { + padding: 2px 5px; + background: rgba(27,31,35,0.05); + color: #f47466; +} +.container pre { + padding: 10px 20px; +} +.container pre code { + padding: 0; + background: none; + color: var(--hl-color); + text-shadow: none; +} +.container figure.highlight { + position: relative; + border-radius: 6px; +} +.container figure.highlight pre { + margin: 0; + padding: 8px 0; + border: none; +} +.container figure.highlight figcaption, +.container figure.highlight .caption { + padding: 6px 0 2px 14px; + font-size: var(--global-font-size); + line-height: 1em; +} +.container figure.highlight figcaption a, +.container figure.highlight .caption a { + float: right; + padding-right: 10px; + color: var(--hl-color); +} +.container figure.highlight figcaption a:hover, +.container figure.highlight .caption a:hover { + border-bottom-color: var(--hl-color); +} +.container figure.highlight.copy-true { + -webkit-user-select: all; + -moz-user-select: all; + -ms-user-select: all; + user-select: all; + -webkit-user-select: all; +} +.container figure.highlight.copy-true > table, +.container figure.highlight.copy-true > pre { + display: block !important; + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); +} +.container .highlight-tools { + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-align: center; + -moz-box-align: center; + -o-box-align: center; + -ms-flex-align: center; + -webkit-align-items: center; + align-items: center; + padding: 0 8px; + min-height: 24px; + height: 2.15em; + background: var(--hltools-bg); + color: var(--hltools-color); + font-size: var(--global-font-size); + overflow: hidden; +} +.container .highlight-tools > * { + padding: 5px; +} +.container .highlight-tools i { + cursor: pointer; + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; +} +.container .highlight-tools i:hover { + color: #49b1f5; +} +.container .highlight-tools.closed ~ * { + display: none; +} +.container .highlight-tools.closed .expand { + -webkit-transform: rotate(-90deg); + -moz-transform: rotate(-90deg); + -o-transform: rotate(-90deg); + -ms-transform: rotate(-90deg); + transform: rotate(-90deg); +} +.container .highlight-tools > .macStyle { + padding: 0; +} +.container .highlight-tools .code-lang { + -webkit-box-flex: 1; + -moz-box-flex: 1; + -o-box-flex: 1; + box-flex: 1; + -webkit-flex: 1; + -ms-flex: 1; + flex: 1; + text-transform: uppercase; + font-weight: bold; + font-size: 1.15em; + -webkit-user-select: none; + -moz-user-select: none; + -ms-user-select: none; + user-select: none; + -webkit-user-select: none; + padding: 2px; +} +.container .highlight-tools .copy-notice { + padding-right: 2px; + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transition: opacity 0.4s; + -moz-transition: opacity 0.4s; + -o-transition: opacity 0.4s; + -ms-transition: opacity 0.4s; + transition: opacity 0.4s; +} +.container .highlight-tools .code-lang { + -webkit-box-flex: 1; + -moz-box-flex: 1; + -o-box-flex: 1; + box-flex: 1; + -webkit-flex: 1; + -ms-flex: 1; + flex: 1; +} +.container .gutter { + -webkit-user-select: none; + -moz-user-select: none; + -ms-user-select: none; + user-select: none; + -webkit-user-select: none; +} +.container .gist table { + width: auto; +} +.container .gist table td { + border: none; +} +.article-sort { + margin-left: 10px; + padding-left: 20px; + border-left: 2px solid #aadafa; +} +.article-sort-title { + position: relative; + margin-left: 10px; + padding-bottom: 20px; + padding-left: 20px; + font-size: 1.72em; +} +.article-sort-title:hover:before { + border-color: var(--pseudo-hover); +} +.article-sort-title:before { + position: absolute; + top: calc(((100% - 36px) / 2)); + left: -9px; + z-index: 1; + width: 10px; + height: 10px; + border: 5px solid #49b1f5; + border-radius: 10px; + background: var(--card-bg); + content: ''; + line-height: 10px; + -webkit-transition: all 0.2s ease-in-out; + -moz-transition: all 0.2s ease-in-out; + -o-transition: all 0.2s ease-in-out; + -ms-transition: all 0.2s ease-in-out; + transition: all 0.2s ease-in-out; +} +.article-sort-title:after { + position: absolute; + bottom: 0; + left: 0; + z-index: 0; + width: 2px; + height: 1.5em; + background: #aadafa; + content: ''; +} +.article-sort-item { + position: relative; + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-align: center; + -moz-box-align: center; + -o-box-align: center; + -ms-flex-align: center; + -webkit-align-items: center; + align-items: center; + margin: 0 0 20px 10px; + -webkit-transition: all 0.2s ease-in-out; + -moz-transition: all 0.2s ease-in-out; + -o-transition: all 0.2s ease-in-out; + -ms-transition: all 0.2s ease-in-out; + transition: all 0.2s ease-in-out; +} +.article-sort-item:hover:before { + border-color: var(--pseudo-hover); +} +.article-sort-item:before { + position: absolute; + left: calc(-20px - 17px); + width: 6px; + height: 6px; + border: 3px solid #49b1f5; + border-radius: 6px; + background: var(--card-bg); + content: ''; + -webkit-transition: all 0.2s ease-in-out; + -moz-transition: all 0.2s ease-in-out; + -o-transition: all 0.2s ease-in-out; + -ms-transition: all 0.2s ease-in-out; + transition: all 0.2s ease-in-out; +} +.article-sort-item.no-article-cover { + height: 80px; +} +.article-sort-item.no-article-cover .article-sort-item-info { + padding: 0; +} +.article-sort-item.year { + font-size: 1.43em; + margin-bottom: 10px; +} +.article-sort-item.year:hover:before { + border-color: #49b1f5; +} +.article-sort-item.year:before { + border-color: var(--pseudo-hover); +} +.article-sort-item-time { + color: var(--card-meta); + font-size: 0.85em; +} +.article-sort-item-time time { + padding-left: 6px; + cursor: default; +} +.article-sort-item-title { + color: var(--font-color); + font-size: 1.05em; + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; + -webkit-line-clamp: 2; +} +.article-sort-item-title:hover { + color: #49b1f5; + -webkit-transform: translateX(10px); + -moz-transform: translateX(10px); + -o-transform: translateX(10px); + -ms-transform: translateX(10px); + transform: translateX(10px); +} +.article-sort-item-img { + overflow: hidden; + width: 100px; + height: 70px; + border-radius: 6px; +} +@media screen and (max-width: 768px) { + .article-sort-item-img { + width: 70px; + height: 70px; + } +} +.article-sort-item-info { + -webkit-box-flex: 1; + -moz-box-flex: 1; + -o-box-flex: 1; + box-flex: 1; + -webkit-flex: 1; + -ms-flex: 1; + flex: 1; + padding: 0 16px; +} +.category-lists .category-title { + font-size: 2.57em; +} +@media screen and (max-width: 768px) { + .category-lists .category-title { + font-size: 2em; + } +} +.category-lists .category-list { + margin-bottom: 0; +} +.category-lists .category-list a { + color: var(--font-color); +} +.category-lists .category-list a:hover { + color: #49b1f5; +} +.category-lists .category-list .category-list-count { + margin-left: 8px; + color: var(--card-meta); +} +.category-lists .category-list .category-list-count:before { + content: '('; +} +.category-lists .category-list .category-list-count:after { + content: ')'; +} +.category-lists ul { + padding: 0 0 0 20px; +} +.category-lists ul ul { + padding-left: 4px; +} +.category-lists ul li { + position: relative; + margin: 6px 0; + padding: 0.12em 0.4em 0.12em 1.4em; +} +#body-wrap { + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-orient: vertical; + -moz-box-orient: vertical; + -o-box-orient: vertical; + -webkit-flex-direction: column; + -ms-flex-direction: column; + flex-direction: column; + min-height: 100vh; +} +.layout { + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-flex: 1; + -moz-box-flex: 1; + -o-box-flex: 1; + box-flex: 1; + -webkit-flex: 1 auto; + -ms-flex: 1 auto; + flex: 1 auto; + margin: 0 auto; + padding: 40px 15px; + max-width: 1200px; + width: 100%; +} +@media screen and (max-width: 900px) { + .layout { + -webkit-box-orient: vertical; + -moz-box-orient: vertical; + -o-box-orient: vertical; + -webkit-flex-direction: column; + -ms-flex-direction: column; + flex-direction: column; + } +} +@media screen and (max-width: 768px) { + .layout { + padding: 20px 5px; + } +} +@media screen and (min-width: 2000px) { + .layout { + max-width: 70%; + } +} +.layout > div:first-child:not(.nc) { + -webkit-align-self: flex-start; + align-self: flex-start; + -ms-flex-item-align: start; + padding: 50px 40px; +} +@media screen and (max-width: 768px) { + .layout > div:first-child:not(.nc) { + padding: 36px 14px; + } +} +.layout > div:first-child { + width: 74%; + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; +} +@media screen and (max-width: 900px) { + .layout > div:first-child { + width: 100% !important; + } +} +.layout.hide-aside { + max-width: 1000px; +} +@media screen and (min-width: 2000px) { + .layout.hide-aside { + max-width: 1300px; + } +} +.layout.hide-aside > div { + width: 100% !important; +} +.apple #page-header.full_page { + background-attachment: scroll !important; +} +.apple .recent-post-item, +.apple .avatar-img, +.apple .flink-item-icon { + -webkit-transform: translateZ(0); + -moz-transform: translateZ(0); + -o-transform: translateZ(0); + -ms-transform: translateZ(0); + transform: translateZ(0); +} +.container .flink { + margin-bottom: 20px; +} +.container .flink .flink-list { + overflow: auto; + padding: 10px 10px 0; + text-align: center; +} +.container .flink .flink-list > .flink-list-item { + position: relative; + float: left; + overflow: hidden; + margin: 15px 7px; + width: calc(100% / 3 - 15px); + height: 90px; + line-height: 17px; + -webkit-transform: translateZ(0); + border-radius: 8px; +} +@media screen and (max-width: 1024px) { + .container .flink .flink-list > .flink-list-item { + width: calc(50% - 15px) !important; + } +} +@media screen and (max-width: 600px) { + .container .flink .flink-list > .flink-list-item { + width: calc(100% - 15px) !important; + } +} +.container .flink .flink-list > .flink-list-item:hover .flink-item-icon { + margin-left: -10px; + width: 0; +} +.container .flink .flink-list > .flink-list-item:before { + position: absolute; + top: 0; + right: 0; + bottom: 0; + left: 0; + z-index: -1; + background: var(--text-bg-hover); + content: ''; + -webkit-transition: -webkit-transform 0.3s ease-out; + -moz-transition: -moz-transform 0.3s ease-out; + -o-transition: -o-transform 0.3s ease-out; + -ms-transition: -ms-transform 0.3s ease-out; + transition: transform 0.3s ease-out; + -webkit-transform: scale(0); + -moz-transform: scale(0); + -o-transform: scale(0); + -ms-transform: scale(0); + transform: scale(0); +} +.container .flink .flink-list > .flink-list-item:hover:before, +.container .flink .flink-list > .flink-list-item:focus:before, +.container .flink .flink-list > .flink-list-item:active:before { + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); +} +.container .flink .flink-list > .flink-list-item a { + color: var(--font-color); + text-decoration: none; +} +.container .flink .flink-list > .flink-list-item a .flink-item-icon { + float: left; + overflow: hidden; + margin: 15px 10px; + width: 60px; + height: 60px; + border-radius: 7px; + -webkit-transition: width 0.3s ease-out; + -moz-transition: width 0.3s ease-out; + -o-transition: width 0.3s ease-out; + -ms-transition: width 0.3s ease-out; + transition: width 0.3s ease-out; +} +.container .flink .flink-list > .flink-list-item a .flink-item-icon img { + width: 100%; + height: 100%; + -webkit-transition: filter 375ms ease-in 0.2s, -webkit-transform 0.3s; + -moz-transition: filter 375ms ease-in 0.2s, -moz-transform 0.3s; + -o-transition: filter 375ms ease-in 0.2s, -o-transform 0.3s; + -ms-transition: filter 375ms ease-in 0.2s, -ms-transform 0.3s; + transition: filter 375ms ease-in 0.2s, transform 0.3s; + object-fit: cover; +} +.container .flink .flink-list > .flink-list-item a .img-alt { + display: none; +} +.container .flink .flink-item-name { + padding: 16px 10px 0 0; + height: 40px; + font-weight: bold; + font-size: 1.43em; +} +.container .flink .flink-item-desc { + padding: 16px 10px 16px 0; + height: 50px; + font-size: 0.93em; +} +.container .flink .flink-name { + margin-bottom: 5px; + font-weight: bold; + font-size: 1.5em; +} +#recent-posts .recent-post-item { + position: relative; + overflow: hidden; + margin-bottom: 20px; + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-orient: horizontal; + -moz-box-orient: horizontal; + -o-box-orient: horizontal; + -webkit-flex-direction: row; + -ms-flex-direction: row; + flex-direction: row; + -webkit-box-align: center; + -moz-box-align: center; + -o-box-align: center; + -ms-flex-align: center; + -webkit-align-items: center; + align-items: center; + height: 16.8em; +} +@media screen and (max-width: 768px) { + #recent-posts .recent-post-item { + -webkit-box-orient: vertical; + -moz-box-orient: vertical; + -o-box-orient: vertical; + -webkit-flex-direction: column; + -ms-flex-direction: column; + flex-direction: column; + height: auto; + } +} +@media screen and (min-width: 2000px) { + #recent-posts .recent-post-item { + height: 18.8em; + } +} +#recent-posts .recent-post-item:hover .post-bg { + -webkit-transform: scale(1.1); + -moz-transform: scale(1.1); + -o-transform: scale(1.1); + -ms-transform: scale(1.1); + transform: scale(1.1); +} +#recent-posts .recent-post-item.ads-wrap { + display: block !important; + height: auto !important; +} +#recent-posts .recent-post-item .post_cover { + overflow: hidden; + width: 42%; + height: 100%; +} +@media screen and (max-width: 768px) { + #recent-posts .recent-post-item .post_cover { + width: 100%; + height: 230px; + } +} +#recent-posts .recent-post-item .post_cover.right { + -webkit-box-ordinal-group: 1; + -moz-box-ordinal-group: 1; + -o-box-ordinal-group: 1; + -ms-flex-order: 1; + -webkit-order: 1; + order: 1; +} +@media screen and (max-width: 768px) { + #recent-posts .recent-post-item .post_cover.right { + -webkit-box-ordinal-group: 0; + -moz-box-ordinal-group: 0; + -o-box-ordinal-group: 0; + -ms-flex-order: 0; + -webkit-order: 0; + order: 0; + } +} +#recent-posts .recent-post-item .post_cover .post-bg { + z-index: -4; +} +#recent-posts .recent-post-item >.recent-post-info { + padding: 0 40px; + width: 58%; +} +@media screen and (max-width: 768px) { + #recent-posts .recent-post-item >.recent-post-info { + padding: 20px 20px 30px; + width: 100%; + } +} +#recent-posts .recent-post-item >.recent-post-info.no-cover { + width: 100%; +} +@media screen and (max-width: 768px) { + #recent-posts .recent-post-item >.recent-post-info.no-cover { + padding: 30px 20px; + } +} +#recent-posts .recent-post-item >.recent-post-info > .article-title { + color: var(--text-highlight-color); + font-size: 1.55em; + line-height: 1.4; + -webkit-transition: all 0.2s ease-in-out; + -moz-transition: all 0.2s ease-in-out; + -o-transition: all 0.2s ease-in-out; + -ms-transition: all 0.2s ease-in-out; + transition: all 0.2s ease-in-out; + -webkit-line-clamp: 2; +} +#recent-posts .recent-post-item >.recent-post-info > .article-title .sticky { + margin-right: 10px; + color: #ff7242; + -webkit-transform: rotate(45deg); + -moz-transform: rotate(45deg); + -o-transform: rotate(45deg); + -ms-transform: rotate(45deg); + transform: rotate(45deg); +} +@media screen and (max-width: 768px) { + #recent-posts .recent-post-item >.recent-post-info > .article-title { + font-size: 1.43em; + } +} +#recent-posts .recent-post-item >.recent-post-info > .article-title:hover { + color: #49b1f5; +} +#recent-posts .recent-post-item >.recent-post-info > .article-meta-wrap { + margin: 6px 0; + color: var(--card-meta); + font-size: 0.9em; +} +#recent-posts .recent-post-item >.recent-post-info > .article-meta-wrap > .post-meta-date { + cursor: default; +} +#recent-posts .recent-post-item >.recent-post-info > .article-meta-wrap i { + margin: 0 4px 0 0; +} +#recent-posts .recent-post-item >.recent-post-info > .article-meta-wrap .fa-spinner { + margin: 0; +} +#recent-posts .recent-post-item >.recent-post-info > .article-meta-wrap .article-meta-label { + padding-right: 4px; +} +#recent-posts .recent-post-item >.recent-post-info > .article-meta-wrap .article-meta-separator { + margin: 0 6px; +} +#recent-posts .recent-post-item >.recent-post-info > .article-meta-wrap .article-meta-link { + margin: 0 4px; +} +#recent-posts .recent-post-item >.recent-post-info > .article-meta-wrap a { + color: var(--card-meta); +} +#recent-posts .recent-post-item >.recent-post-info > .article-meta-wrap a:hover { + color: #49b1f5; + text-decoration: underline; +} +#recent-posts .recent-post-item >.recent-post-info > .content { + -webkit-line-clamp: 2; +} +#article-container .shuoshuo-item { + margin-bottom: 20px; + padding: 35px 30px 30px; +} +@media screen and (max-width: 768px) { + #article-container .shuoshuo-item { + padding: 25px 20px 20px; + } +} +#article-container .shuoshuo-item-header { + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-align: center; + -moz-box-align: center; + -o-box-align: center; + -ms-flex-align: center; + -webkit-align-items: center; + align-items: center; + cursor: default; +} +#article-container .shuoshuo-avatar { + overflow: hidden; + width: 40px; + height: 40px; + border-radius: 40px; +} +#article-container .shuoshuo-avatar img { + margin: 0; + width: 100%; + height: 100%; +} +#article-container .shuoshuo-info { + margin-left: 10px; + line-height: 1.5; +} +#article-container .shuoshuo-date { + color: #858585; + font-size: 0.8em; +} +#article-container .shuoshuo-content { + padding: 15px 0 10px; +} +#article-container .shuoshuo-content > *:last-child { + margin-bottom: 0; +} +#article-container .shuoshuo-footer { + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-align: center; + -moz-box-align: center; + -o-box-align: center; + -ms-flex-align: center; + -webkit-align-items: center; + align-items: center; +} +#article-container .shuoshuo-footer.flex-between { + -webkit-box-pack: justify; + -moz-box-pack: justify; + -o-box-pack: justify; + -ms-flex-pack: justify; + -webkit-justify-content: space-between; + justify-content: space-between; +} +#article-container .shuoshuo-footer.flex-end { + -webkit-box-pack: end; + -moz-box-pack: end; + -o-box-pack: end; + -ms-flex-pack: end; + -webkit-justify-content: flex-end; + justify-content: flex-end; +} +#article-container .shuoshuo-footer .shuoshuo-tag { + display: inline-block; + margin-right: 8px; + padding: 0 8px; + width: fit-content; + border: 1px solid #49b1f5; + border-radius: 12px; + color: #49b1f5; + font-size: 0.85em; + cursor: default; + -webkit-transition: all 0.2s ease-in-out; + -moz-transition: all 0.2s ease-in-out; + -o-transition: all 0.2s ease-in-out; + -ms-transition: all 0.2s ease-in-out; + transition: all 0.2s ease-in-out; +} +#article-container .shuoshuo-footer .shuoshuo-tag:hover { + background: #49b1f5; + color: var(--white); +} +#article-container .shuoshuo-footer .shuoshuo-comment-btn { + padding: 2px; + color: #90a4ae; + cursor: pointer; +} +#article-container .shuoshuo-footer .shuoshuo-comment-btn:hover { + color: #49b1f5; +} +#article-container .shuoshuo-comment { + padding-top: 10px; +} +#article-container .shuoshuo-comment.no-comment { + display: none; +} +.tag-cloud-list a { + display: inline-block; + margin: 2px; + padding: 2px 7px; + line-height: 1.7; + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; + border-radius: 5px; +} +.tag-cloud-list a:hover { + background: var(--btn-bg) !important; + -webkit-box-shadow: 2px 2px 6px rgba(0,0,0,0.2); + box-shadow: 2px 2px 6px rgba(0,0,0,0.2); + color: var(--btn-color) !important; +} +@media screen and (max-width: 768px) { + .tag-cloud-list a { + zoom: 0.85; + } +} +.tag-cloud-title { + font-size: 2.57em; +} +@media screen and (max-width: 768px) { + .tag-cloud-title { + font-size: 2em; + } +} +.page-title + .tag-cloud-list { + text-align: left; +} +#aside-content { + width: 26%; +} +@media screen and (min-width: 900px) { + #aside-content { + padding-left: 15px; + } +} +@media screen and (max-width: 900px) { + #aside-content { + margin-top: 20px; + width: 100%; + } +} +#aside-content .card-widget { + position: relative; + overflow: hidden; + margin-bottom: 20px; + padding: 20px 24px; +} +#aside-content .card-widget:last-child { + margin-bottom: 0; +} +#aside-content .card-info .author-info-name { + font-weight: 500; + font-size: 1.57em; +} +#aside-content .card-info .author-info-description { + margin-top: -0.42em; +} +#aside-content .card-info .site-data { + margin: 14px 0 4px; +} +#aside-content .card-info .card-info-social-icons { + margin: 6px 0 -6px; +} +#aside-content .card-info .card-info-social-icons .social-icon { + margin: 0 10px; + color: var(--font-color); + font-size: 1.4em; +} +#aside-content .card-info .card-info-social-icons i { + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; +} +#aside-content .card-info .card-info-social-icons i:hover { + -webkit-transform: rotate(360deg); + -moz-transform: rotate(360deg); + -o-transform: rotate(360deg); + -ms-transform: rotate(360deg); + transform: rotate(360deg); +} +#aside-content .card-info #card-info-btn { + display: block; + margin-top: 14px; + background-color: var(--btn-bg); + color: var(--btn-color); + text-align: center; + line-height: 2.4; + border-radius: 7px; +} +#aside-content .card-info #card-info-btn:hover { + background-color: var(--btn-hover-color); +} +#aside-content .card-info #card-info-btn span { + padding-left: 10px; +} +#aside-content .item-headline { + padding-bottom: 6px; + font-size: 1.2em; +} +#aside-content .item-headline span { + margin-left: 6px; +} +@media screen and (min-width: 900px) { + #aside-content .sticky_layout { + position: sticky; + position: -webkit-sticky; + top: 20px; + -webkit-transition: top 0.3s; + -moz-transition: top 0.3s; + -o-transition: top 0.3s; + -ms-transition: top 0.3s; + transition: top 0.3s; + } +} +#aside-content .card-tag-cloud a { + display: inline-block; + padding: 0 4px; + line-height: 1.8; +} +#aside-content .card-tag-cloud a:hover { + color: #49b1f5 !important; +} +#aside-content .aside-list > span { + display: block; + margin-bottom: 10px; + text-align: center; +} +#aside-content .aside-list > .aside-list-item { + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-align: center; + -moz-box-align: center; + -o-box-align: center; + -ms-flex-align: center; + -webkit-align-items: center; + align-items: center; + padding: 6px 0; +} +#aside-content .aside-list > .aside-list-item:first-child { + padding-top: 0; +} +#aside-content .aside-list > .aside-list-item:not(:last-child) { + border-bottom: 1px dashed #f5f5f5; +} +#aside-content .aside-list > .aside-list-item:last-child { + padding-bottom: 0; +} +#aside-content .aside-list > .aside-list-item .thumbnail { + overflow: hidden; + width: 4em; + height: 4em; + border-radius: 6px; +} +#aside-content .aside-list > .aside-list-item .content { + -webkit-box-flex: 1; + -moz-box-flex: 1; + -o-box-flex: 1; + box-flex: 1; + -webkit-flex: 1; + -ms-flex: 1; + flex: 1; + padding-left: 10px; + word-break: break-all; +} +#aside-content .aside-list > .aside-list-item .content > .name { + -webkit-line-clamp: 1; +} +#aside-content .aside-list > .aside-list-item .content > time, +#aside-content .aside-list > .aside-list-item .content > .name { + display: block; + color: var(--card-meta); + font-size: 0.85em; +} +#aside-content .aside-list > .aside-list-item .content > .title, +#aside-content .aside-list > .aside-list-item .content > .comment { + color: var(--font-color); + line-height: 1.5; + -webkit-line-clamp: 2; +} +#aside-content .aside-list > .aside-list-item .content > .title:hover, +#aside-content .aside-list > .aside-list-item .content > .comment:hover { + color: #49b1f5; +} +#aside-content .aside-list > .aside-list-item.no-cover { + min-height: 4.4em; +} +#aside-content .card-archives ul.card-archive-list, +#aside-content .card-categories ul.card-category-list { + margin: 0; + padding: 0; + list-style: none; +} +#aside-content .card-archives ul.card-archive-list > .card-archive-list-item a, +#aside-content .card-categories ul.card-category-list > .card-category-list-item a { + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-orient: horizontal; + -moz-box-orient: horizontal; + -o-box-orient: horizontal; + -webkit-flex-direction: row; + -ms-flex-direction: row; + flex-direction: row; + margin: 2px 0; + padding: 2px 8px; + color: var(--font-color); + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; + border-radius: 6px; +} +#aside-content .card-archives ul.card-archive-list > .card-archive-list-item a:hover, +#aside-content .card-categories ul.card-category-list > .card-category-list-item a:hover { + padding: 2px 12px; + background-color: var(--text-bg-hover); + color: var(--white); +} +#aside-content .card-archives ul.card-archive-list > .card-archive-list-item a span:first-child, +#aside-content .card-categories ul.card-category-list > .card-category-list-item a span:first-child { + -webkit-box-flex: 1; + -moz-box-flex: 1; + -o-box-flex: 1; + box-flex: 1; + -webkit-flex: 1; + -ms-flex: 1; + flex: 1; +} +#aside-content .card-categories .card-category-list.child { + padding: 0 0 0 16px; +} +#aside-content .card-categories .card-category-list > .parent > a.expand i { + -webkit-transform: rotate(-90deg); + -moz-transform: rotate(-90deg); + -o-transform: rotate(-90deg); + -ms-transform: rotate(-90deg); + transform: rotate(-90deg); +} +#aside-content .card-categories .card-category-list > .parent > a.expand + .child { + display: block; +} +#aside-content .card-categories .card-category-list > .parent > a .card-category-list-name { + width: 70% !important; +} +#aside-content .card-categories .card-category-list > .parent > a .card-category-list-count { + width: calc(100% - 70% - 20px); + text-align: right; +} +#aside-content .card-categories .card-category-list > .parent > a i { + float: right; + margin-right: -0.5em; + padding: 0.5em; + -webkit-transition: -webkit-transform 0.3s; + -moz-transition: -moz-transform 0.3s; + -o-transition: -o-transform 0.3s; + -ms-transition: -ms-transform 0.3s; + transition: transform 0.3s; + -webkit-transform: rotate(0); + -moz-transform: rotate(0); + -o-transform: rotate(0); + -ms-transform: rotate(0); + transform: rotate(0); +} +#aside-content .card-webinfo .webinfo .webinfo-item { + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-align: center; + -moz-box-align: center; + -o-box-align: center; + -ms-flex-align: center; + -webkit-align-items: center; + align-items: center; + padding: 2px 10px 0; +} +#aside-content .card-webinfo .webinfo .webinfo-item div:first-child { + -webkit-box-flex: 1; + -moz-box-flex: 1; + -o-box-flex: 1; + box-flex: 1; + -webkit-flex: 1; + -ms-flex: 1; + flex: 1; + padding-right: 20px; +} +@media screen and (min-width: 901px) { + #aside-content #card-toc { + right: 0 !important; + } +} +@media screen and (max-width: 900px) { + #aside-content #card-toc { + position: fixed; + right: 55px; + bottom: 30px; + z-index: 100; + max-width: 380px; + max-height: calc(100% - 60px); + width: calc(100% - 80px); + -webkit-transition: none; + -moz-transition: none; + -o-transition: none; + -ms-transition: none; + transition: none; + -webkit-transform: scale(0); + -moz-transform: scale(0); + -o-transform: scale(0); + -ms-transform: scale(0); + transform: scale(0); + -webkit-transform-origin: right bottom; + -moz-transform-origin: right bottom; + -o-transform-origin: right bottom; + -ms-transform-origin: right bottom; + transform-origin: right bottom; + } + #aside-content #card-toc.open { + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } +} +#aside-content #card-toc .toc-percentage { + float: right; + margin-top: -9px; + color: #a9a9a9; + font-style: italic; + font-size: 140%; +} +#aside-content #card-toc .toc-content { + overflow-y: scroll; + overflow-y: overlay; + margin: 0 -24px; + max-height: calc(100vh - 120px); + width: calc(100% + 48px); +} +@media screen and (max-width: 900px) { + #aside-content #card-toc .toc-content { + max-height: calc(100vh - 140px); + } +} +#aside-content #card-toc .toc-content > * { + margin: 0 20px !important; +} +#aside-content #card-toc .toc-content > * > .toc-item > .toc-child { + margin-left: 10px; + padding-left: 10px; + border-left: 1px solid var(--dark-grey); +} +#aside-content #card-toc .toc-content:not(.is-expand) .toc-child { + display: none; +} +@media screen and (max-width: 900px) { + #aside-content #card-toc .toc-content:not(.is-expand) .toc-child { + display: block !important; + } +} +#aside-content #card-toc .toc-content:not(.is-expand) .toc-item.active .toc-child { + display: block; +} +#aside-content #card-toc .toc-content ol, +#aside-content #card-toc .toc-content li { + list-style: none; +} +#aside-content #card-toc .toc-content > ol { + padding: 0 !important; +} +#aside-content #card-toc .toc-content ol { + margin: 0; + padding-left: 18px; +} +#aside-content #card-toc .toc-content .toc-link { + display: block; + margin: 4px 0; + padding: 1px 8px; + color: var(--toc-link-color); + -webkit-transition: all 0.2s ease-in-out; + -moz-transition: all 0.2s ease-in-out; + -o-transition: all 0.2s ease-in-out; + -ms-transition: all 0.2s ease-in-out; + transition: all 0.2s ease-in-out; + border-radius: 6px; +} +#aside-content #card-toc .toc-content .toc-link:hover { + color: #49b1f5; +} +#aside-content #card-toc .toc-content .toc-link.active { + background: #00c4b6; + color: #fff; +} +#aside-content .sticky_layout:only-child > :first-child { + margin-top: 0; +} +#aside-content .card-more-btn { + float: right; + color: inherit; +} +#aside-content .card-more-btn:hover { + -webkit-animation: more-btn-move 1s infinite; + -moz-animation: more-btn-move 1s infinite; + -o-animation: more-btn-move 1s infinite; + -ms-animation: more-btn-move 1s infinite; + animation: more-btn-move 1s infinite; +} +#aside-content .card-announcement .item-headline i { + color: #f00; +} +.avatar-img { + overflow: hidden; + margin: 0 auto; + width: 110px; + height: 110px; + border-radius: 70px; +} +.avatar-img img { + width: 100%; + height: 100%; + -webkit-transition: filter 375ms ease-in 0.2s, -webkit-transform 0.3s; + -moz-transition: filter 375ms ease-in 0.2s, -moz-transform 0.3s; + -o-transition: filter 375ms ease-in 0.2s, -o-transform 0.3s; + -ms-transition: filter 375ms ease-in 0.2s, -ms-transform 0.3s; + transition: filter 375ms ease-in 0.2s, transform 0.3s; + object-fit: cover; +} +.avatar-img img:hover { + -webkit-transform: rotate(360deg); + -moz-transform: rotate(360deg); + -o-transform: rotate(360deg); + -ms-transform: rotate(360deg); + transform: rotate(360deg); +} +.site-data { + display: table; + width: 100%; + table-layout: fixed; +} +.site-data > a { + display: table-cell; +} +.site-data > a div { + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; +} +.site-data > a:hover div { + color: #49b1f5 !important; +} +.site-data > a .headline { + color: var(--font-color); + font-size: 0.95em; +} +.site-data > a .length-num { + margin-top: -0.45em; + color: var(--text-highlight-color); + font-size: 1.2em; +} +@media screen and (min-width: 900px) { + html.hide-aside .layout { + -webkit-box-pack: center; + -moz-box-pack: center; + -o-box-pack: center; + -ms-flex-pack: center; + -webkit-justify-content: center; + justify-content: center; + } + html.hide-aside .layout > .aside-content { + display: none; + } + html.hide-aside .layout > div:first-child { + width: 80%; + } +} +.page .sticky_layout { + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-orient: vertical; + -moz-box-orient: vertical; + -o-box-orient: vertical; + -webkit-flex-direction: column; + -ms-flex-direction: column; + flex-direction: column; +} +@-moz-keyframes more-btn-move { + 0%, 100% { + -webkit-transform: translateX(0); + -moz-transform: translateX(0); + -o-transform: translateX(0); + -ms-transform: translateX(0); + transform: translateX(0); + } + 50% { + -webkit-transform: translateX(3px); + -moz-transform: translateX(3px); + -o-transform: translateX(3px); + -ms-transform: translateX(3px); + transform: translateX(3px); + } +} +@-webkit-keyframes more-btn-move { + 0%, 100% { + -webkit-transform: translateX(0); + -moz-transform: translateX(0); + -o-transform: translateX(0); + -ms-transform: translateX(0); + transform: translateX(0); + } + 50% { + -webkit-transform: translateX(3px); + -moz-transform: translateX(3px); + -o-transform: translateX(3px); + -ms-transform: translateX(3px); + transform: translateX(3px); + } +} +@-o-keyframes more-btn-move { + 0%, 100% { + -webkit-transform: translateX(0); + -moz-transform: translateX(0); + -o-transform: translateX(0); + -ms-transform: translateX(0); + transform: translateX(0); + } + 50% { + -webkit-transform: translateX(3px); + -moz-transform: translateX(3px); + -o-transform: translateX(3px); + -ms-transform: translateX(3px); + transform: translateX(3px); + } +} +@keyframes more-btn-move { + 0%, 100% { + -webkit-transform: translateX(0); + -moz-transform: translateX(0); + -o-transform: translateX(0); + -ms-transform: translateX(0); + transform: translateX(0); + } + 50% { + -webkit-transform: translateX(3px); + -moz-transform: translateX(3px); + -o-transform: translateX(3px); + -ms-transform: translateX(3px); + transform: translateX(3px); + } +} +@-moz-keyframes toc-open { + 0% { + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } + 100% { + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } +} +@-webkit-keyframes toc-open { + 0% { + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } + 100% { + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } +} +@-o-keyframes toc-open { + 0% { + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } + 100% { + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } +} +@keyframes toc-open { + 0% { + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } + 100% { + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } +} +@-moz-keyframes toc-close { + 0% { + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } + 100% { + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } +} +@-webkit-keyframes toc-close { + 0% { + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } + 100% { + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } +} +@-o-keyframes toc-close { + 0% { + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } + 100% { + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } +} +@keyframes toc-close { + 0% { + -webkit-transform: scale(1); + -moz-transform: scale(1); + -o-transform: scale(1); + -ms-transform: scale(1); + transform: scale(1); + } + 100% { + -webkit-transform: scale(0.7); + -moz-transform: scale(0.7); + -o-transform: scale(0.7); + -ms-transform: scale(0.7); + transform: scale(0.7); + } +} +#post-comment .comment-head { + margin-bottom: 20px; +} +#post-comment .comment-head:after { + display: block; + clear: both; + content: ''; +} +#post-comment .comment-head .comment-headline { + display: inline-block; + vertical-align: middle; + font-weight: 700; + font-size: 1.43em; +} +#post-comment .comment-head .comment-switch { + display: inline-block; + float: right; + margin: 2px auto 0; + padding: 4px 16px; + width: max-content; + border-radius: 8px; + background: #f6f8fa; +} +#post-comment .comment-head .comment-switch .first-comment { + color: #49b1f5; +} +#post-comment .comment-head .comment-switch .second-comment { + color: #ff7242; +} +#post-comment .comment-head .comment-switch #switch-btn { + position: relative; + display: inline-block; + margin: -4px 8px 0; + width: 42px; + height: 22px; + border-radius: 34px; + background-color: #49b1f5; + vertical-align: middle; + cursor: pointer; + -webkit-transition: 0.4s; + -moz-transition: 0.4s; + -o-transition: 0.4s; + -ms-transition: 0.4s; + transition: 0.4s; +} +#post-comment .comment-head .comment-switch #switch-btn:before { + position: absolute; + bottom: 4px; + left: 4px; + width: 14px; + height: 14px; + border-radius: 50%; + background-color: #fff; + content: ''; + -webkit-transition: 0.4s; + -moz-transition: 0.4s; + -o-transition: 0.4s; + -ms-transition: 0.4s; + transition: 0.4s; +} +#post-comment .comment-wrap > div { + -webkit-animation: tabshow 0.5s; + -moz-animation: tabshow 0.5s; + -o-animation: tabshow 0.5s; + -ms-animation: tabshow 0.5s; + animation: tabshow 0.5s; +} +#post-comment .comment-wrap > div:nth-child(2) { + display: none; +} +#post-comment.move #switch-btn { + background-color: #ff7242; +} +#post-comment.move #switch-btn:before { + -webkit-transform: translateX(20px); + -moz-transform: translateX(20px); + -o-transform: translateX(20px); + -ms-transform: translateX(20px); + transform: translateX(20px); +} +#post-comment.move .comment-wrap > div:first-child { + display: none; +} +#post-comment.move .comment-wrap > div:last-child { + display: block; +} +#footer { + position: relative; + background-color: #49b1f5; + background-attachment: scroll; + background-position: bottom; + background-size: cover; +} +#footer:before { + position: absolute; + width: 100%; + height: 100%; + background-color: var(--mark-bg); + content: ''; +} +#footer-wrap { + position: relative; + padding: 40px 20px; + color: var(--light-grey); + text-align: center; +} +#footer-wrap a { + color: var(--light-grey); +} +#footer-wrap a:hover { + text-decoration: underline; +} +#footer-wrap .footer-separator { + margin: 0 4px; +} +#footer-wrap .icp-icon { + padding: 0 4px; + max-height: 1.4em; + width: auto; + vertical-align: text-bottom; +} +#page-header { + position: relative; + width: 100%; + background-color: #49b1f5; + background-position: center center; + background-size: cover; + background-repeat: no-repeat; + -webkit-transition: all 0.5s; + -moz-transition: all 0.5s; + -o-transition: all 0.5s; + -ms-transition: all 0.5s; + transition: all 0.5s; +} +#page-header:not(.not-top-img):before { + position: absolute; + width: 100%; + height: 100%; + background-color: var(--mark-bg); + content: ''; +} +#page-header.full_page { + height: 100vh; + background-attachment: fixed; +} +#page-header.full_page #site-info { + position: absolute; + top: 43%; + padding: 0 10px; + width: 100%; +} +#page-header #site-title, +#page-header #site-subtitle, +#page-header #scroll-down .scroll-down-effects { + text-align: center; + text-shadow: 2px 2px 4px rgba(0,0,0,0.15); + line-height: 1.5; +} +#page-header #site-title { + margin: 0; + color: var(--white); + font-size: 1.85em; +} +@media screen and (min-width: 768px) { + #page-header #site-title { + font-size: 2.85em; + } +} +#page-header #site-subtitle { + color: var(--light-grey); + font-size: 1.15em; +} +@media screen and (min-width: 768px) { + #page-header #site-subtitle { + font-size: 1.72em; + } +} +#page-header #site_social_icons { + display: none; + margin: 0 auto; + text-align: center; +} +@media screen and (max-width: 768px) { + #page-header #site_social_icons { + display: block; + } +} +#page-header #site_social_icons .social-icon { + margin: 0 10px; + color: var(--light-grey); + text-shadow: 2px 2px 4px rgba(0,0,0,0.15); + font-size: 1.43em; +} +#page-header #scroll-down { + position: absolute; + bottom: 10px; + width: 100%; + cursor: pointer; +} +#page-header #scroll-down .scroll-down-effects { + position: relative; + width: 100%; + color: var(--light-grey); + font-size: 20px; +} +#page-header.not-home-page { + height: 400px; +} +@media screen and (max-width: 768px) { + #page-header.not-home-page { + height: 280px; + } +} +#page-header #page-site-info { + position: absolute; + top: 200px; + padding: 0 10px; + width: 100%; +} +@media screen and (max-width: 768px) { + #page-header #page-site-info { + top: 140px; + } +} +#page-header.post-bg { + height: 400px; +} +@media screen and (max-width: 768px) { + #page-header.post-bg { + height: 360px; + } +} +#page-header #post-info { + position: absolute; + width: 100%; + bottom: 30px; +} +#page-header #post-info > * { + margin: 0 auto; + padding: 0 15px; + max-width: 1200px; +} +@media screen and (min-width: 768px) and (max-width: 1300px) { + #page-header #post-info > * { + padding: 0 30px; + } +} +@media screen and (min-width: 2000px) { + #page-header #post-info > * { + max-width: 70%; + } +} +#page-header.not-top-img { + margin-bottom: 10px; + height: 60px; + background: 0; +} +#page-header.not-top-img .title-seo { + display: none; +} +#page-header.not-top-img #nav { + background: rgba(255,255,255,0.8); + -webkit-box-shadow: 0 5px 6px -5px rgba(133,133,133,0.6); + box-shadow: 0 5px 6px -5px rgba(133,133,133,0.6); +} +#page-header.not-top-img #nav a, +#page-header.not-top-img #nav span.site-page, +#page-header.not-top-img #nav .site-name { + color: var(--font-color); + text-shadow: none; +} +#page-header.nav-fixed #nav { + position: fixed; + top: -60px; + z-index: 91; + background: rgba(255,255,255,0.7); + -webkit-box-shadow: 0 5px 6px -5px rgba(133,133,133,0.6); + box-shadow: 0 5px 6px -5px rgba(133,133,133,0.6); + -webkit-transition: -webkit-transform 0.2s ease-in-out, opacity 0.2s ease-in-out; + -moz-transition: -moz-transform 0.2s ease-in-out, opacity 0.2s ease-in-out; + -o-transition: -o-transform 0.2s ease-in-out, opacity 0.2s ease-in-out; + -ms-transition: -ms-transform 0.2s ease-in-out, opacity 0.2s ease-in-out; + transition: transform 0.2s ease-in-out, opacity 0.2s ease-in-out; + will-change: transform; + backdrop-filter: blur(7px); +} +#page-header.nav-fixed #nav #blog-info { + color: var(--font-color); +} +#page-header.nav-fixed #nav #blog-info:hover { + color: #49b1f5; +} +#page-header.nav-fixed #nav #blog-info .site-name { + text-shadow: none; +} +#page-header.nav-fixed #nav #blog-info > a:first-child { + display: none; +} +#page-header.nav-fixed #nav #blog-info > a:last-child { + display: inline; +} +#page-header.nav-fixed #nav a, +#page-header.nav-fixed #nav span.site-page, +#page-header.nav-fixed #nav #toggle-menu { + color: var(--font-color); + text-shadow: none; +} +#page-header.nav-fixed #nav a:hover, +#page-header.nav-fixed #nav span.site-page:hover, +#page-header.nav-fixed #nav #toggle-menu:hover { + color: #49b1f5; +} +#page-header.nav-fixed.fixed #nav { + top: 0; + -webkit-transition: all 0.5s; + -moz-transition: all 0.5s; + -o-transition: all 0.5s; + -ms-transition: all 0.5s; + transition: all 0.5s; +} +#page-header.nav-visible:not(.fixed) #nav { + -webkit-transition: all 0.5s; + -moz-transition: all 0.5s; + -o-transition: all 0.5s; + -ms-transition: all 0.5s; + transition: all 0.5s; + -webkit-transform: translate3d(0, 100%, 0); + -moz-transform: translate3d(0, 100%, 0); + -o-transform: translate3d(0, 100%, 0); + -ms-transform: translate3d(0, 100%, 0); + transform: translate3d(0, 100%, 0); +} +#page-header.nav-visible:not(.fixed) + .layout > .aside-content > .sticky_layout { + top: 70px; + -webkit-transition: top 0.5s; + -moz-transition: top 0.5s; + -o-transition: top 0.5s; + -ms-transition: top 0.5s; + transition: top 0.5s; +} +#page-header.fixed #nav { + position: fixed; +} +#page-header.fixed + .layout > .aside-content > .sticky_layout { + top: 70px; + -webkit-transition: top 0.5s; + -moz-transition: top 0.5s; + -o-transition: top 0.5s; + -ms-transition: top 0.5s; + transition: top 0.5s; +} +#page-header.fixed + .layout #card-toc .toc-content { + max-height: calc(100vh - 170px); +} +#page .page-title { + margin: 0 0 10px; + font-weight: bold; + font-size: 2em; +} +#post > #post-info { + margin-bottom: 30px; +} +#post > #post-info .post-title { + padding-bottom: 4px; + border-bottom: 1px solid var(--light-grey); + color: var(--text-highlight-color); +} +#post > #post-info .post-title .post-edit-link { + float: right; +} +#post > #post-info #post-meta, +#post > #post-info #post-meta a { + color: #78818a; +} +#post-info .post-title { + margin-bottom: 8px; + color: var(--white); + font-weight: normal; + font-size: 2.5em; + line-height: 1.5; + -webkit-line-clamp: 3; +} +@media screen and (max-width: 768px) { + #post-info .post-title { + font-size: 2.1em; + } +} +#post-info .post-title .post-edit-link { + padding-left: 10px; +} +#post-info #post-meta { + color: var(--light-grey); + font-size: 95%; +} +@media screen and (min-width: 768px) { + #post-info #post-meta > .meta-secondline > span:first-child { + display: none; + } +} +@media screen and (max-width: 768px) { + #post-info #post-meta { + font-size: 90%; + } + #post-info #post-meta > .meta-firstline, + #post-info #post-meta > .meta-secondline { + display: inline; + } +} +#post-info #post-meta .post-meta-separator { + margin: 0 5px; +} +#post-info #post-meta .post-meta-icon { + margin-right: 4px; +} +#post-info #post-meta .post-meta-label { + margin-right: 4px; +} +#post-info #post-meta a { + color: var(--light-grey); + -webkit-transition: all 0.3s ease-out; + -moz-transition: all 0.3s ease-out; + -o-transition: all 0.3s ease-out; + -ms-transition: all 0.3s ease-out; + transition: all 0.3s ease-out; +} +#post-info #post-meta a:hover { + color: #49b1f5; + text-decoration: underline; +} +#nav { + position: absolute; + top: 0; + z-index: 90; + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-align: center; + -moz-box-align: center; + -o-box-align: center; + -ms-flex-align: center; + -webkit-align-items: center; + align-items: center; + padding: 0 36px; + width: 100%; + height: 60px; + font-size: 1.3em; + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transition: all 0.5s; + -moz-transition: all 0.5s; + -o-transition: all 0.5s; + -ms-transition: all 0.5s; + transition: all 0.5s; +} +@media screen and (max-width: 768px) { + #nav { + padding: 0 16px; + } +} +#nav.show { + opacity: 1; + -ms-filter: none; + filter: none; +} +#nav #blog-info { + -webkit-box-flex: 1; + -moz-box-flex: 1; + -o-box-flex: 1; + box-flex: 1; + -webkit-flex: 1; + -ms-flex: 1; + flex: 1; + color: var(--light-grey); +} +#nav #blog-info .site-icon { + margin-right: 6px; + height: 36px; + vertical-align: middle; +} +#nav #blog-info .nav-page-title { + display: none; +} +#nav #toggle-menu { + display: none; + padding: 2px 0 0 6px; + vertical-align: top; +} +#nav #toggle-menu:hover { + color: var(--white); +} +#nav a, +#nav span.site-page { + color: var(--light-grey); +} +#nav a:hover, +#nav span.site-page:hover { + color: var(--white); +} +#nav .site-name { + text-shadow: 2px 2px 4px rgba(0,0,0,0.15); + font-weight: bold; +} +#nav .menus_items { + display: inline; +} +#nav .menus_items .menus_item { + position: relative; + display: inline-block; + padding: 0 0 0 14px; +} +#nav .menus_items .menus_item:hover .menus_item_child { + display: block; +} +#nav .menus_items .menus_item:hover > span > i:last-child { + -webkit-transform: rotate(180deg); + -moz-transform: rotate(180deg); + -o-transform: rotate(180deg); + -ms-transform: rotate(180deg); + transform: rotate(180deg); +} +#nav .menus_items .menus_item > span > i:last-child { + padding: 4px; + -webkit-transition: -webkit-transform 0.3s; + -moz-transition: -moz-transform 0.3s; + -o-transition: -o-transform 0.3s; + -ms-transition: -ms-transform 0.3s; + transition: transform 0.3s; +} +#nav .menus_items .menus_item .menus_item_child { + position: absolute; + right: 0; + display: none; + margin-top: 8px; + padding: 0; + width: max-content; + background-color: var(--sidebar-bg); + -webkit-box-shadow: 0 5px 20px -4px rgba(0,0,0,0.5); + box-shadow: 0 5px 20px -4px rgba(0,0,0,0.5); + -webkit-animation: sub_menus 0.3s 0.1s ease both; + -moz-animation: sub_menus 0.3s 0.1s ease both; + -o-animation: sub_menus 0.3s 0.1s ease both; + -ms-animation: sub_menus 0.3s 0.1s ease both; + animation: sub_menus 0.3s 0.1s ease both; + border-radius: 5px; +} +#nav .menus_items .menus_item .menus_item_child:before { + position: absolute; + top: -8px; + left: 0; + width: 100%; + height: 20px; + content: ''; +} +#nav .menus_items .menus_item .menus_item_child li { + list-style: none; +} +#nav .menus_items .menus_item .menus_item_child li:hover { + background: var(--text-bg-hover); +} +#nav .menus_items .menus_item .menus_item_child li:first-child { + border-top-left-radius: 5px; + border-top-right-radius: 5px; +} +#nav .menus_items .menus_item .menus_item_child li:last-child { + border-bottom-right-radius: 5px; + border-bottom-left-radius: 5px; +} +#nav .menus_items .menus_item .menus_item_child li a { + display: inline-block; + padding: 8px 16px; + width: 100%; + color: var(--font-color) !important; + text-shadow: none !important; +} +#nav.hide-menu #toggle-menu { + display: inline-block !important; +} +#nav.hide-menu #toggle-menu .site-page { + font-size: inherit; +} +#nav.hide-menu .menus_items { + display: none; +} +#nav.hide-menu #search-button span:not(.site-page) { + display: none; +} +#nav #search-button { + display: inline; + padding: 0 0 0 14px; +} +#nav .site-page { + position: relative; + padding-bottom: 6px; + text-shadow: 1px 1px 2px rgba(0,0,0,0.3); + font-size: 0.78em; + cursor: pointer; +} +#nav .site-page:not(.child):after { + position: absolute; + bottom: 0; + left: 0; + z-index: -1; + width: 0; + height: 3px; + background-color: #80c8f8; + content: ''; + -webkit-transition: all 0.3s ease-in-out; + -moz-transition: all 0.3s ease-in-out; + -o-transition: all 0.3s ease-in-out; + -ms-transition: all 0.3s ease-in-out; + transition: all 0.3s ease-in-out; + border-radius: 6px; +} +#nav .site-page:not(.child):hover:after { + width: 100%; +} +#pagination .pagination { + margin-top: 20px; + text-align: center; +} +#pagination .page-number.current { + background: #00c4b6; + color: var(--white); +} +#pagination .full-width { + width: 100% !important; +} +#pagination .pagination-related { + width: 50%; + height: 150px; +} +@media screen and (max-width: 768px) { + #pagination .pagination-related { + width: 100%; + } +} +#pagination .pagination-related .info-1 .info-item-2 { + -webkit-line-clamp: 1; +} +#pagination .pagination-related .info-2 .info-item-1 { + -webkit-line-clamp: 2; +} +#pagination.pagination-post { + overflow: hidden; + margin-top: 40px; + width: 100%; + border-radius: 6px; +} +.layout .pagination > * { + display: inline-block; + margin: 0 6px; + width: 2.5em; + height: 2.5em; + line-height: 2.5em; +} +.layout .pagination > *:not(.space):hover { + background: var(--btn-hover-color); + color: var(--btn-color); +} +#archive .pagination { + margin-top: 30px; +} +#archive .pagination > *:not(.space) { + -webkit-box-shadow: none; + box-shadow: none; +} +.pagination-related { + position: relative; + display: inline-block; + overflow: hidden; + background: #000; + vertical-align: bottom; +} +.pagination-related.next-post .info { + text-align: right; +} +.pagination-related .info .info-1, +.pagination-related .info .info-2 { + padding: 20px 40px; + color: var(--white); + -webkit-transition: -webkit-transform 0.3s, opacity 0.3s; + -moz-transition: -moz-transform 0.3s, opacity 0.3s; + -o-transition: -o-transform 0.3s, opacity 0.3s; + -ms-transition: -ms-transform 0.3s, opacity 0.3s; + transition: transform 0.3s, opacity 0.3s; +} +.pagination-related .info .info-1 .info-item-1 { + color: var(--light-grey); + text-transform: uppercase; + font-size: 90%; +} +.pagination-related .info .info-1 .info-item-2 { + color: var(--white); + font-weight: 500; +} +.pagination-related .info .info-2 { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: translate(0, 0); + -moz-transform: translate(0, 0); + -o-transform: translate(0, 0); + -ms-transform: translate(0, 0); + transform: translate(0, 0); +} +.pagination-related:not(.no-desc):hover .info-1 { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transform: translate(0, -100%); + -moz-transform: translate(0, -100%); + -o-transform: translate(0, -100%); + -ms-transform: translate(0, -100%); + transform: translate(0, -100%); +} +.pagination-related:not(.no-desc):hover .info-2 { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translate(0, -50%); + -moz-transform: translate(0, -50%); + -o-transform: translate(0, -50%); + -ms-transform: translate(0, -50%); + transform: translate(0, -50%); +} +.container { + word-wrap: break-word; + overflow-wrap: break-word; +} +.container a { + color: #49b1f5; +} +.container a:hover { + text-decoration: underline; +} +.container img { + display: block; + margin: 0 auto 20px; + max-width: 100%; + -webkit-transition: filter 375ms ease-in 0.2s; + -moz-transition: filter 375ms ease-in 0.2s; + -o-transition: filter 375ms ease-in 0.2s; + -ms-transition: filter 375ms ease-in 0.2s; + transition: filter 375ms ease-in 0.2s; + border-radius: 6px; +} +.container p { + margin: 0 0 16px; +} +.container iframe { + margin: 0 0 20px; +} +.container kbd { + margin: 0 3px; + padding: 3px 5px; + border: 1px solid #b4b4b4; + background-color: #f8f8f8; + -webkit-box-shadow: 0 1px 3px rgba(0,0,0,0.25), 0 2px 1px 0 rgba(255,255,255,0.6) inset; + box-shadow: 0 1px 3px rgba(0,0,0,0.25), 0 2px 1px 0 rgba(255,255,255,0.6) inset; + color: #34495e; + white-space: nowrap; + font-weight: 600; + font-size: 0.9em; + font-family: Monaco, 'Ubuntu Mono', monospace; + line-height: 1em; + border-radius: 3px; +} +.container ol ol, +.container ul ol, +.container ol ul, +.container ul ul { + padding-left: 20px; +} +.container ol li, +.container ul li { + margin: 4px 0; +} +.container ol p, +.container ul p { + margin: 0 0 8px; +} +.container > :last-child { + margin-bottom: 0 !important; +} +.container hr { + margin: 20px 0; +} +.container h1, +.container h2, +.container h3, +.container h4, +.container h5, +.container h6 { + -webkit-transition: all 0.2s ease-out; + -moz-transition: all 0.2s ease-out; + -o-transition: all 0.2s ease-out; + -ms-transition: all 0.2s ease-out; + transition: all 0.2s ease-out; +} +.container h1:before, +.container h2:before, +.container h3:before, +.container h4:before, +.container h5:before, +.container h6:before { + position: absolute; + top: calc(50% - 7px); + left: 0; + color: #f47466; + content: '\f0c1'; + line-height: 1; + -webkit-transition: all 0.2s ease-out; + -moz-transition: all 0.2s ease-out; + -o-transition: all 0.2s ease-out; + -ms-transition: all 0.2s ease-out; + transition: all 0.2s ease-out; +} +.container h1:hover:before, +.container h2:hover:before, +.container h3:hover:before, +.container h4:hover:before, +.container h5:hover:before, +.container h6:hover:before { + color: #49b1f5; +} +.container h1 { + padding-left: 28px; +} +.container h1:before { + font-size: 18px; +} +.container h1:hover { + padding-left: 32px; +} +.container h2 { + padding-left: 26px; +} +.container h2:before { + font-size: 16px; +} +.container h2:hover { + padding-left: 30px; +} +.container h3 { + padding-left: 24px; +} +.container h3:before { + font-size: 14px; +} +.container h3:hover { + padding-left: 28px; +} +.container h4 { + padding-left: 22px; +} +.container h4:before { + font-size: 12px; +} +.container h4:hover { + padding-left: 26px; +} +.container h5 { + padding-left: 20px; +} +.container h5:before { + font-size: 10px; +} +.container h5:hover { + padding-left: 24px; +} +.container h6 { + padding-left: 20px; +} +.container h6:before { + font-size: 10px; +} +.container h6:hover { + padding-left: 24px; +} +.container ol p, +.container ul p { + margin: 0 0 8px; +} +.container li::marker { + color: #49b1f5; + font-weight: 600; + font-size: 1.05em; +} +.container li:hover::marker { + color: var(--pseudo-hover); +} +.container ul > li { + list-style-type: circle; +} +#post .tag_share:after { + display: block; + clear: both; + content: ''; +} +#post .tag_share .post-meta__tag-list { + display: inline-block; +} +#post .tag_share .post-meta__tags { + display: inline-block; + margin: 8px 8px 8px 0; + padding: 0 12px; + width: fit-content; + border: 1px solid #49b1f5; + border-radius: 12px; + color: #49b1f5; + font-size: 0.85em; + -webkit-transition: all 0.2s ease-in-out; + -moz-transition: all 0.2s ease-in-out; + -o-transition: all 0.2s ease-in-out; + -ms-transition: all 0.2s ease-in-out; + transition: all 0.2s ease-in-out; +} +#post .tag_share .post-meta__tags:hover { + background: #49b1f5; + color: var(--white); +} +#post .tag_share .post-share { + display: inline-block; + float: right; + margin: 8px 0 0; + width: fit-content; +} +#post .tag_share .post-share .social-share { + font-size: 0.85em; +} +#post .tag_share .post-share .social-share .social-share-icon { + margin: 0 4px; + width: 1.85em; + height: 1.85em; + font-size: 1.2em; + line-height: 1.85em; +} +#post .post-copyright { + position: relative; + margin: 40px 0 10px; + padding: 10px 16px; + border: 1px solid var(--light-grey); + -webkit-transition: box-shadow 0.3s ease-in-out; + -moz-transition: box-shadow 0.3s ease-in-out; + -o-transition: box-shadow 0.3s ease-in-out; + -ms-transition: box-shadow 0.3s ease-in-out; + transition: box-shadow 0.3s ease-in-out; + border-radius: 6px; +} +#post .post-copyright:before { + position: absolute; + top: 2px; + right: 12px; + color: #49b1f5; + content: '\f1f9'; + font-size: 1.3em; +} +#post .post-copyright:hover { + -webkit-box-shadow: 0 0 8px 0 rgba(232,237,250,0.6), 0 2px 4px 0 rgba(232,237,250,0.5); + box-shadow: 0 0 8px 0 rgba(232,237,250,0.6), 0 2px 4px 0 rgba(232,237,250,0.5); +} +#post .post-copyright .post-copyright-meta { + color: #49b1f5; + font-weight: bold; +} +#post .post-copyright .post-copyright-meta i { + margin-right: 3px; +} +#post .post-copyright .post-copyright-info { + padding-left: 6px; +} +#post .post-copyright .post-copyright-info a { + text-decoration: underline; + word-break: break-word; +} +#post .post-copyright .post-copyright-info a:hover { + text-decoration: none; +} +#post #post-outdate-notice { + position: relative; + margin: 0 0 20px; + padding: 0.5em 1.2em; + background-color: #ffe6e6; + color: #f66; + border-radius: 3px; + padding: 0.5em 1em 0.5em 2.6em; + border-left: 5px solid #ff8080; +} +#post #post-outdate-notice .num { + padding: 0 4px; +} +#post #post-outdate-notice:before { + position: absolute; + top: 50%; + left: 0.9em; + color: #ff8080; + content: '\f071'; + -webkit-transform: translateY(-50%); + -moz-transform: translateY(-50%); + -o-transform: translateY(-50%); + -ms-transform: translateY(-50%); + transform: translateY(-50%); +} +#post .ads-wrap { + margin: 40px 0; +} +.relatedPosts { + margin-top: 40px; +} +.relatedPosts > .headline { + margin-bottom: 5px; + font-weight: 700; + font-size: 1.43em; +} +.relatedPosts > .relatedPosts-list > a { + margin: 3px; + width: calc(33.333% - 6px); + height: 200px; + border-radius: 6px; +} +@media screen and (max-width: 768px) { + .relatedPosts > .relatedPosts-list > a { + margin: 2px; + width: calc(50% - 4px); + height: 150px; + } +} +@media screen and (max-width: 600px) { + .relatedPosts > .relatedPosts-list > a { + width: calc(100% - 4px); + } +} +.relatedPosts > .relatedPosts-list .info .info-1 .info-item-2 { + -webkit-line-clamp: 2; +} +.relatedPosts > .relatedPosts-list .info .info-2 .info-item-1 { + -webkit-line-clamp: 3; +} +.post-reward { + position: relative; + margin-top: 80px; + width: 100%; + text-align: center; + pointer-events: none; +} +.post-reward > * { + pointer-events: auto; +} +.post-reward .reward-button { + display: inline-block; + padding: 4px 24px; + background: var(--btn-bg); + color: var(--btn-color); + cursor: pointer; + border-radius: 6px; +} +.post-reward .reward-button i { + margin-right: 5px; +} +.post-reward:hover .reward-button { + background: var(--btn-hover-color); +} +.post-reward:hover > .reward-main { + display: block; +} +.post-reward .reward-main { + position: absolute; + bottom: 40px; + left: 0; + z-index: 100; + display: none; + padding: 0 0 15px; + width: 100%; + border-radius: 6px; +} +.post-reward .reward-main .reward-all { + display: inline-block; + margin: 0; + padding: 20px 10px; + background: var(--reward-pop); +} +.post-reward .reward-main .reward-all:before { + position: absolute; + bottom: -10px; + left: 0; + width: 100%; + height: 20px; + content: ''; +} +.post-reward .reward-main .reward-all:after { + position: absolute; + right: 0; + bottom: 2px; + left: 0; + margin: 0 auto; + width: 0; + height: 0; + border-top: 13px solid var(--reward-pop); + border-right: 13px solid transparent; + border-left: 13px solid transparent; + content: ''; +} +.post-reward .reward-main .reward-all .reward-item { + display: inline-block; + padding: 0 8px; + list-style-type: none; + vertical-align: top; +} +.post-reward .reward-main .reward-all .reward-item img { + width: 130px; + height: 130px; +} +.post-reward .reward-main .reward-all .reward-item .post-qr-code-desc { + width: 130px; + color: #858585; +} +#rightside { + position: fixed; + right: -48px; + bottom: 40px; + z-index: 100; + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transition: all 0.5s; + -moz-transition: all 0.5s; + -o-transition: all 0.5s; + -ms-transition: all 0.5s; + transition: all 0.5s; +} +#rightside.rightside-show { + opacity: 0.8; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=80)"; + filter: alpha(opacity=80); + -webkit-transform: translate(-58px, 0); + -moz-transform: translate(-58px, 0); + -o-transform: translate(-58px, 0); + -ms-transform: translate(-58px, 0); + transform: translate(-58px, 0); +} +#rightside #rightside-config-hide { + height: 0; + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transition: -webkit-transform 0.4s; + -moz-transition: -moz-transform 0.4s; + -o-transition: -o-transform 0.4s; + -ms-transition: -ms-transform 0.4s; + transition: transform 0.4s; + -webkit-transform: translate(45px, 0); + -moz-transform: translate(45px, 0); + -o-transform: translate(45px, 0); + -ms-transform: translate(45px, 0); + transform: translate(45px, 0); +} +#rightside #rightside-config-hide.show { + height: auto; + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translate(0, 0); + -moz-transform: translate(0, 0); + -o-transform: translate(0, 0); + -ms-transform: translate(0, 0); + transform: translate(0, 0); +} +#rightside #rightside-config-hide.status { + height: auto; + opacity: 1; + -ms-filter: none; + filter: none; +} +#rightside > div > button, +#rightside > div > a { + display: block; + margin-bottom: 5px; + width: 35px; + height: 35px; + background-color: var(--btn-bg); + color: var(--btn-color); + text-align: center; + font-size: 16px; + line-height: 35px; + border-radius: 5px; +} +#rightside > div > button:hover, +#rightside > div > a:hover { + background-color: var(--btn-hover-color); +} +#rightside #mobile-toc-button { + display: none; +} +@media screen and (max-width: 900px) { + #rightside #mobile-toc-button { + display: block; + } +} +@media screen and (max-width: 900px) { + #rightside #hide-aside-btn { + display: none; + } +} +#sidebar #menu-mask { + position: fixed; + z-index: 102; + display: none; + width: 100%; + height: 100%; + background: rgba(0,0,0,0.8); +} +#sidebar #sidebar-menus { + position: fixed; + top: 0; + right: -330px; + z-index: 103; + overflow-x: hidden; + overflow-y: scroll; + padding-left: 5px; + width: 330px; + height: 100%; + background: var(--sidebar-bg); + -webkit-transition: all 0.5s; + -moz-transition: all 0.5s; + -o-transition: all 0.5s; + -ms-transition: all 0.5s; + transition: all 0.5s; +} +#sidebar #sidebar-menus.open { + -webkit-transform: translate3d(-100%, 0, 0); + -moz-transform: translate3d(-100%, 0, 0); + -o-transform: translate3d(-100%, 0, 0); + -ms-transform: translate3d(-100%, 0, 0); + transform: translate3d(-100%, 0, 0); +} +#sidebar #sidebar-menus > .avatar-img { + margin: 20px auto; +} +#sidebar #sidebar-menus .site-data { + padding: 0 10px; +} +#sidebar #sidebar-menus hr { + margin: 20px auto; +} +#sidebar #sidebar-menus .menus_items { + margin: 20px; + padding: 15px; + background: var(--sidebar-menu-bg); + -webkit-box-shadow: 0 0 1px 1px rgba(7,17,27,0.05); + box-shadow: 0 0 1px 1px rgba(7,17,27,0.05); + border-radius: 10px; +} +#sidebar #sidebar-menus .menus_items .site-page { + position: relative; + display: block; + margin: 4px 0; + padding: 2px 23px 2px 15px; + color: var(--font-color); + font-size: 1.15em; + cursor: pointer; + border-radius: 6px; +} +#sidebar #sidebar-menus .menus_items .site-page:hover { + background: var(--text-bg-hover); + color: var(--white); +} +#sidebar #sidebar-menus .menus_items .site-page i:first-child { + width: 15%; + text-align: left; +} +#sidebar #sidebar-menus .menus_items .site-page.group > i:last-child { + position: absolute; + top: 0.6em; + right: 10px; + -webkit-transition: -webkit-transform 0.3s; + -moz-transition: -moz-transform 0.3s; + -o-transition: -o-transform 0.3s; + -ms-transition: -ms-transform 0.3s; + transition: transform 0.3s; +} +#sidebar #sidebar-menus .menus_items .site-page.group.hide > i:last-child { + -webkit-transform: rotate(90deg); + -moz-transform: rotate(90deg); + -o-transform: rotate(90deg); + -ms-transform: rotate(90deg); + transform: rotate(90deg); +} +#sidebar #sidebar-menus .menus_items .site-page.group.hide + .menus_item_child { + display: none; +} +#sidebar #sidebar-menus .menus_items .menus_item_child { + margin: 0; + padding-left: 25px; + list-style: none; +} +#vcomment { + font-size: 1.1em; +} +#vcomment .vbtn { + border: none; + background: var(--btn-bg); + color: var(--btn-color); +} +#vcomment .vbtn:hover { + background: var(--btn-hover-color); +} +#vcomment .vimg { + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; +} +#vcomment .vimg:hover { + -webkit-transform: rotate(360deg); + -moz-transform: rotate(360deg); + -o-transform: rotate(360deg); + -ms-transform: rotate(360deg); + transform: rotate(360deg); +} +#vcomment .vcards .vcard .vcontent.expand:before, +#vcomment .vcards .vcard .vcontent.expand:after { + z-index: 22; +} +#waline-wrap { + --waline-font-size: 1.1em; + --waline-theme-color: #49b1f5; + --waline-active-color: #ff7242; +} +#waline-wrap .wl-comment-actions > button:not(last-child) { + padding-right: 4px; +} +.twikoo .tk-content p { + margin: 3px 0; +} +.fireworks { + position: fixed; + top: 0; + left: 0; + z-index: 9999; + pointer-events: none; +} +.medium-zoom-image--opened { + z-index: 99999 !important; + margin: 0 !important; +} +.medium-zoom-overlay { + z-index: 99999 !important; +} +.utterances, +.fb-comments iframe { + width: 100% !important; +} +#gitalk-container .gt-meta { + margin: 0 0 0.8em; + padding: 6px 0 16px; +} +.katex-display { + overflow: auto hidden; + padding: 5px; +} +.katex-display .katex-show { + display: block; +} +.katex { + display: none; +} +.katex.katex-show { + display: inline; +} +mjx-container { + overflow-x: auto; + overflow-y: hidden; + padding-bottom: 4px; + max-width: 100%; +} +mjx-container[display] { + display: block !important; + min-width: auto !important; +} +mjx-container:not([display]) { + display: inline-grid !important; +} +mjx-assistive-mml { + right: 0; + bottom: 0; +} +.aplayer { + color: #4c4948; +} +.container .aplayer { + margin: 0 0 20px; +} +.container .aplayer ol, +.container .aplayer ul { + margin: 0; + padding: 0; +} +.container .aplayer ol li, +.container .aplayer ul li { + margin: 0; + padding: 0 15px; +} +.container .aplayer ol li:before, +.container .aplayer ul li:before { + content: none; +} +.snackbar-container.snackbar-css { + border-radius: 5px; + opacity: 0.85 !important; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=85)" !important; + filter: alpha(opacity=85) !important; +} +.abc-music-sheet { + margin: 0 0 20px; + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transition: opacity 0.3s; + -moz-transition: opacity 0.3s; + -o-transition: opacity 0.3s; + -ms-transition: opacity 0.3s; + transition: opacity 0.3s; +} +.abc-music-sheet.abcjs-container { + opacity: 1; + -ms-filter: none; + filter: none; +} +@media screen and (max-width: 768px) { + .fancybox__toolbar__column.is-middle { + display: none; + } +} +.container .btn-center { + margin: 0 0 20px; + text-align: center; +} +.container .btn-beautify { + display: inline-block; + margin: 0 4px 6px; + padding: 0 15px; + background-color: var(--btn-beautify-color, #777); + color: #fff; + line-height: 2; + border-radius: 6px; +} +.container .btn-beautify.blue { + --btn-beautify-color: #428bca; +} +.container .btn-beautify.pink { + --btn-beautify-color: #ff69b4; +} +.container .btn-beautify.red { + --btn-beautify-color: #f00; +} +.container .btn-beautify.purple { + --btn-beautify-color: #6f42c1; +} +.container .btn-beautify.orange { + --btn-beautify-color: #ff8c00; +} +.container .btn-beautify.green { + --btn-beautify-color: #5cb85c; +} +.container .btn-beautify:hover { + background-color: var(--btn-hover-color); +} +.container .btn-beautify i + span { + margin-left: 6px; +} +.container .btn-beautify:not(.block) + .btn-beautify:not(.block) { + margin: 0 4px 20px; +} +.container .btn-beautify.block { + display: block; + margin: 0 0 20px; + width: fit-content; + width: -moz-fit-content; +} +.container .btn-beautify.block.center { + margin: 0 auto 20px; +} +.container .btn-beautify.block.right { + margin: 0 0 20px auto; +} +.container .btn-beautify.larger { + padding: 6px 15px; +} +.container .btn-beautify:hover { + text-decoration: none; +} +.container .btn-beautify.outline { + border: 1px solid transparent; + border-color: var(--btn-beautify-color, #777); + background-color: transparent; + color: var(--btn-beautify-color, #777); +} +.container .btn-beautify.outline:hover { + background-color: var(--btn-beautify-color, #777); +} +.container .btn-beautify.outline:hover { + color: #fff !important; +} +.container figure.gallery-group { + position: relative; + float: left; + overflow: hidden; + margin: 6px 4px; + width: calc(50% - 8px); + height: 250px; + border-radius: 10px; + background: #000; + -webkit-transform: translate3d(0, 0, 0); +} +@media screen and (max-width: 600px) { + .container figure.gallery-group { + width: calc(100% - 8px); + } +} +@media screen and (min-width: 1024px) { + .container figure.gallery-group { + width: calc(100% / 3 - 8px); + } +} +.container figure.gallery-group:hover img { + opacity: 0.4; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=40)"; + filter: alpha(opacity=40); + -webkit-transform: translate3d(0, 0, 0); + -moz-transform: translate3d(0, 0, 0); + -o-transform: translate3d(0, 0, 0); + -ms-transform: translate3d(0, 0, 0); + transform: translate3d(0, 0, 0); +} +.container figure.gallery-group:hover .gallery-group-name::after { + -webkit-transform: translate3d(0, 0, 0); + -moz-transform: translate3d(0, 0, 0); + -o-transform: translate3d(0, 0, 0); + -ms-transform: translate3d(0, 0, 0); + transform: translate3d(0, 0, 0); +} +.container figure.gallery-group:hover p { + opacity: 1; + -ms-filter: none; + filter: none; + -webkit-transform: translate3d(0, 0, 0); + -moz-transform: translate3d(0, 0, 0); + -o-transform: translate3d(0, 0, 0); + -ms-transform: translate3d(0, 0, 0); + transform: translate3d(0, 0, 0); +} +.container figure.gallery-group img { + position: relative; + margin: 0; + max-width: none; + width: calc(100% + 20px); + height: 250px; + -webkit-backface-visibility: hidden; + -moz-backface-visibility: hidden; + -ms-backface-visibility: hidden; + backface-visibility: hidden; + opacity: 0.8; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=80)"; + filter: alpha(opacity=80); + -webkit-transition: all 0.3s, filter 375ms ease-in 0.2s; + -moz-transition: all 0.3s, filter 375ms ease-in 0.2s; + -o-transition: all 0.3s, filter 375ms ease-in 0.2s; + -ms-transition: all 0.3s, filter 375ms ease-in 0.2s; + transition: all 0.3s, filter 375ms ease-in 0.2s; + -webkit-transform: translate3d(-10px, 0, 0); + -moz-transform: translate3d(-10px, 0, 0); + -o-transform: translate3d(-10px, 0, 0); + -ms-transform: translate3d(-10px, 0, 0); + transform: translate3d(-10px, 0, 0); + object-fit: cover; +} +.container figure.gallery-group figcaption { + position: absolute; + top: 0; + left: 0; + padding: 30px; + width: 100%; + height: 100%; + color: #fff; + text-transform: uppercase; + -webkit-backface-visibility: hidden; + -moz-backface-visibility: hidden; + -ms-backface-visibility: hidden; + backface-visibility: hidden; +} +.container figure.gallery-group figcaption > a { + position: absolute; + top: 0; + right: 0; + bottom: 0; + left: 0; + z-index: 1000; + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); +} +.container figure.gallery-group p { + margin: 0; + padding: 8px 0 0; + letter-spacing: 1px; + font-size: 1.1em; + line-height: 1.5; + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); + -webkit-transition: opacity 0.35s, -webkit-transform 0.35s; + -moz-transition: opacity 0.35s, -moz-transform 0.35s; + -o-transition: opacity 0.35s, -o-transform 0.35s; + -ms-transition: opacity 0.35s, -ms-transform 0.35s; + transition: opacity 0.35s, transform 0.35s; + -webkit-transform: translate3d(100%, 0, 0); + -moz-transform: translate3d(100%, 0, 0); + -o-transform: translate3d(100%, 0, 0); + -ms-transform: translate3d(100%, 0, 0); + transform: translate3d(100%, 0, 0); + -webkit-line-clamp: 4; +} +.container figure.gallery-group .gallery-group-name { + position: relative; + margin: 0; + padding: 8px 0; + font-weight: bold; + font-size: 1.65em; + line-height: 1.5; + -webkit-line-clamp: 2; +} +.container figure.gallery-group .gallery-group-name:after { + position: absolute; + bottom: 0; + left: 0; + width: 100%; + height: 2px; + background: #fff; + content: ''; + -webkit-transition: -webkit-transform 0.35s; + -moz-transition: -moz-transform 0.35s; + -o-transition: -o-transform 0.35s; + -ms-transition: -ms-transform 0.35s; + transition: transform 0.35s; + -webkit-transform: translate3d(-100%, 0, 0); + -moz-transform: translate3d(-100%, 0, 0); + -o-transform: translate3d(-100%, 0, 0); + -ms-transform: translate3d(-100%, 0, 0); + transform: translate3d(-100%, 0, 0); +} +.container .gallery-group-main { + overflow: auto; + padding: 0 0 16px; +} +.container .gallery-container { + margin: 0 0 20px; + text-align: center; + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); +} +.container .gallery-container.loaded { + opacity: 1; + -ms-filter: none; + filter: none; +} +.container .gallery-container img { + display: initial; + margin: 0; + width: 100%; + height: 100%; +} +.container .gallery-container .gallery-data { + display: none; +} +.container .gallery-container button { + margin-top: 25px; + padding: 8px 14px; + background: var(--btn-bg); + color: var(--btn-color); + font-weight: bold; + font-size: 1.1em; + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; + border-radius: 5px; +} +.container .gallery-container button:hover { + background: var(--btn-hover-color); +} +.container .gallery-container button:hover i { + margin-left: 8px; +} +.container .gallery-container button i { + margin-left: 4px; + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; +} +.container .loading-container { + display: inline-block; + overflow: hidden; + width: 154px; + height: 154px; +} +.container .loading-container .loading-item { + position: relative; + width: 100%; + height: 100%; + -webkit-backface-visibility: hidden; + -moz-backface-visibility: hidden; + -ms-backface-visibility: hidden; + backface-visibility: hidden; + -webkit-transform: translateZ(0) scale(1); + -moz-transform: translateZ(0) scale(1); + -o-transform: translateZ(0) scale(1); + -ms-transform: translateZ(0) scale(1); + transform: translateZ(0) scale(1); + -webkit-transform-origin: 0 0; + -moz-transform-origin: 0 0; + -o-transform-origin: 0 0; + -ms-transform-origin: 0 0; + transform-origin: 0 0; +} +.container .loading-container .loading-item div { + position: absolute; + width: 30.8px; + height: 30.8px; + border-radius: 50%; + background: #e15b64; + -webkit-transform: translate(61.6px, 61.6px) scale(1); + -moz-transform: translate(61.6px, 61.6px) scale(1); + -o-transform: translate(61.6px, 61.6px) scale(1); + -ms-transform: translate(61.6px, 61.6px) scale(1); + transform: translate(61.6px, 61.6px) scale(1); + -webkit-animation: loading-ball 1.92s infinite cubic-bezier(0, 0.5, 0.5, 1); + -moz-animation: loading-ball 1.92s infinite cubic-bezier(0, 0.5, 0.5, 1); + -o-animation: loading-ball 1.92s infinite cubic-bezier(0, 0.5, 0.5, 1); + -ms-animation: loading-ball 1.92s infinite cubic-bezier(0, 0.5, 0.5, 1); + animation: loading-ball 1.92s infinite cubic-bezier(0, 0.5, 0.5, 1); +} +.container .loading-container .loading-item div:nth-child(1) { + background: #f47e60; + -webkit-transform: translate(113.96px, 61.6px) scale(1); + -moz-transform: translate(113.96px, 61.6px) scale(1); + -o-transform: translate(113.96px, 61.6px) scale(1); + -ms-transform: translate(113.96px, 61.6px) scale(1); + transform: translate(113.96px, 61.6px) scale(1); + -webkit-animation: loading-ball-r 0.48s infinite cubic-bezier(0, 0.5, 0.5, 1), loading-ball-c 1.92s infinite step-start; + -moz-animation: loading-ball-r 0.48s infinite cubic-bezier(0, 0.5, 0.5, 1), loading-ball-c 1.92s infinite step-start; + -o-animation: loading-ball-r 0.48s infinite cubic-bezier(0, 0.5, 0.5, 1), loading-ball-c 1.92s infinite step-start; + -ms-animation: loading-ball-r 0.48s infinite cubic-bezier(0, 0.5, 0.5, 1), loading-ball-c 1.92s infinite step-start; + animation: loading-ball-r 0.48s infinite cubic-bezier(0, 0.5, 0.5, 1), loading-ball-c 1.92s infinite step-start; +} +.container .loading-container .loading-item div:nth-child(2) { + background: #e15b64; + -webkit-animation-delay: -0.48s; + -moz-animation-delay: -0.48s; + -o-animation-delay: -0.48s; + -ms-animation-delay: -0.48s; + animation-delay: -0.48s; +} +.container .loading-container .loading-item div:nth-child(3) { + background: #f47e60; + -webkit-animation-delay: -0.96s; + -moz-animation-delay: -0.96s; + -o-animation-delay: -0.96s; + -ms-animation-delay: -0.96s; + animation-delay: -0.96s; +} +.container .loading-container .loading-item div:nth-child(4) { + background: #f8b26a; + -webkit-animation-delay: -1.44s; + -moz-animation-delay: -1.44s; + -o-animation-delay: -1.44s; + -ms-animation-delay: -1.44s; + animation-delay: -1.44s; +} +.container .loading-container .loading-item div:nth-child(5) { + background: #abbd81; + -webkit-animation-delay: -1.92s; + -moz-animation-delay: -1.92s; + -o-animation-delay: -1.92s; + -ms-animation-delay: -1.92s; + animation-delay: -1.92s; +} +@-moz-keyframes loading-ball { + 0% { + -webkit-transform: translate(9.24px, 61.6px) scale(0); + -moz-transform: translate(9.24px, 61.6px) scale(0); + -o-transform: translate(9.24px, 61.6px) scale(0); + -ms-transform: translate(9.24px, 61.6px) scale(0); + transform: translate(9.24px, 61.6px) scale(0); + } + 25% { + -webkit-transform: translate(9.24px, 61.6px) scale(0); + -moz-transform: translate(9.24px, 61.6px) scale(0); + -o-transform: translate(9.24px, 61.6px) scale(0); + -ms-transform: translate(9.24px, 61.6px) scale(0); + transform: translate(9.24px, 61.6px) scale(0); + } + 50% { + -webkit-transform: translate(9.24px, 61.6px) scale(1); + -moz-transform: translate(9.24px, 61.6px) scale(1); + -o-transform: translate(9.24px, 61.6px) scale(1); + -ms-transform: translate(9.24px, 61.6px) scale(1); + transform: translate(9.24px, 61.6px) scale(1); + } + 75% { + -webkit-transform: translate(61.6px, 61.6px) scale(1); + -moz-transform: translate(61.6px, 61.6px) scale(1); + -o-transform: translate(61.6px, 61.6px) scale(1); + -ms-transform: translate(61.6px, 61.6px) scale(1); + transform: translate(61.6px, 61.6px) scale(1); + } + 100% { + -webkit-transform: translate(113.96px, 61.6px) scale(1); + -moz-transform: translate(113.96px, 61.6px) scale(1); + -o-transform: translate(113.96px, 61.6px) scale(1); + -ms-transform: translate(113.96px, 61.6px) scale(1); + transform: translate(113.96px, 61.6px) scale(1); + } +} +@-webkit-keyframes loading-ball { + 0% { + -webkit-transform: translate(9.24px, 61.6px) scale(0); + -moz-transform: translate(9.24px, 61.6px) scale(0); + -o-transform: translate(9.24px, 61.6px) scale(0); + -ms-transform: translate(9.24px, 61.6px) scale(0); + transform: translate(9.24px, 61.6px) scale(0); + } + 25% { + -webkit-transform: translate(9.24px, 61.6px) scale(0); + -moz-transform: translate(9.24px, 61.6px) scale(0); + -o-transform: translate(9.24px, 61.6px) scale(0); + -ms-transform: translate(9.24px, 61.6px) scale(0); + transform: translate(9.24px, 61.6px) scale(0); + } + 50% { + -webkit-transform: translate(9.24px, 61.6px) scale(1); + -moz-transform: translate(9.24px, 61.6px) scale(1); + -o-transform: translate(9.24px, 61.6px) scale(1); + -ms-transform: translate(9.24px, 61.6px) scale(1); + transform: translate(9.24px, 61.6px) scale(1); + } + 75% { + -webkit-transform: translate(61.6px, 61.6px) scale(1); + -moz-transform: translate(61.6px, 61.6px) scale(1); + -o-transform: translate(61.6px, 61.6px) scale(1); + -ms-transform: translate(61.6px, 61.6px) scale(1); + transform: translate(61.6px, 61.6px) scale(1); + } + 100% { + -webkit-transform: translate(113.96px, 61.6px) scale(1); + -moz-transform: translate(113.96px, 61.6px) scale(1); + -o-transform: translate(113.96px, 61.6px) scale(1); + -ms-transform: translate(113.96px, 61.6px) scale(1); + transform: translate(113.96px, 61.6px) scale(1); + } +} +@-o-keyframes loading-ball { + 0% { + -webkit-transform: translate(9.24px, 61.6px) scale(0); + -moz-transform: translate(9.24px, 61.6px) scale(0); + -o-transform: translate(9.24px, 61.6px) scale(0); + -ms-transform: translate(9.24px, 61.6px) scale(0); + transform: translate(9.24px, 61.6px) scale(0); + } + 25% { + -webkit-transform: translate(9.24px, 61.6px) scale(0); + -moz-transform: translate(9.24px, 61.6px) scale(0); + -o-transform: translate(9.24px, 61.6px) scale(0); + -ms-transform: translate(9.24px, 61.6px) scale(0); + transform: translate(9.24px, 61.6px) scale(0); + } + 50% { + -webkit-transform: translate(9.24px, 61.6px) scale(1); + -moz-transform: translate(9.24px, 61.6px) scale(1); + -o-transform: translate(9.24px, 61.6px) scale(1); + -ms-transform: translate(9.24px, 61.6px) scale(1); + transform: translate(9.24px, 61.6px) scale(1); + } + 75% { + -webkit-transform: translate(61.6px, 61.6px) scale(1); + -moz-transform: translate(61.6px, 61.6px) scale(1); + -o-transform: translate(61.6px, 61.6px) scale(1); + -ms-transform: translate(61.6px, 61.6px) scale(1); + transform: translate(61.6px, 61.6px) scale(1); + } + 100% { + -webkit-transform: translate(113.96px, 61.6px) scale(1); + -moz-transform: translate(113.96px, 61.6px) scale(1); + -o-transform: translate(113.96px, 61.6px) scale(1); + -ms-transform: translate(113.96px, 61.6px) scale(1); + transform: translate(113.96px, 61.6px) scale(1); + } +} +@keyframes loading-ball { + 0% { + -webkit-transform: translate(9.24px, 61.6px) scale(0); + -moz-transform: translate(9.24px, 61.6px) scale(0); + -o-transform: translate(9.24px, 61.6px) scale(0); + -ms-transform: translate(9.24px, 61.6px) scale(0); + transform: translate(9.24px, 61.6px) scale(0); + } + 25% { + -webkit-transform: translate(9.24px, 61.6px) scale(0); + -moz-transform: translate(9.24px, 61.6px) scale(0); + -o-transform: translate(9.24px, 61.6px) scale(0); + -ms-transform: translate(9.24px, 61.6px) scale(0); + transform: translate(9.24px, 61.6px) scale(0); + } + 50% { + -webkit-transform: translate(9.24px, 61.6px) scale(1); + -moz-transform: translate(9.24px, 61.6px) scale(1); + -o-transform: translate(9.24px, 61.6px) scale(1); + -ms-transform: translate(9.24px, 61.6px) scale(1); + transform: translate(9.24px, 61.6px) scale(1); + } + 75% { + -webkit-transform: translate(61.6px, 61.6px) scale(1); + -moz-transform: translate(61.6px, 61.6px) scale(1); + -o-transform: translate(61.6px, 61.6px) scale(1); + -ms-transform: translate(61.6px, 61.6px) scale(1); + transform: translate(61.6px, 61.6px) scale(1); + } + 100% { + -webkit-transform: translate(113.96px, 61.6px) scale(1); + -moz-transform: translate(113.96px, 61.6px) scale(1); + -o-transform: translate(113.96px, 61.6px) scale(1); + -ms-transform: translate(113.96px, 61.6px) scale(1); + transform: translate(113.96px, 61.6px) scale(1); + } +} +@-moz-keyframes loading-ball-r { + 0% { + -webkit-transform: translate(113.96px, 61.6px) scale(1); + -moz-transform: translate(113.96px, 61.6px) scale(1); + -o-transform: translate(113.96px, 61.6px) scale(1); + -ms-transform: translate(113.96px, 61.6px) scale(1); + transform: translate(113.96px, 61.6px) scale(1); + } + 100% { + -webkit-transform: translate(113.96px, 61.6px) scale(0); + -moz-transform: translate(113.96px, 61.6px) scale(0); + -o-transform: translate(113.96px, 61.6px) scale(0); + -ms-transform: translate(113.96px, 61.6px) scale(0); + transform: translate(113.96px, 61.6px) scale(0); + } +} +@-webkit-keyframes loading-ball-r { + 0% { + -webkit-transform: translate(113.96px, 61.6px) scale(1); + -moz-transform: translate(113.96px, 61.6px) scale(1); + -o-transform: translate(113.96px, 61.6px) scale(1); + -ms-transform: translate(113.96px, 61.6px) scale(1); + transform: translate(113.96px, 61.6px) scale(1); + } + 100% { + -webkit-transform: translate(113.96px, 61.6px) scale(0); + -moz-transform: translate(113.96px, 61.6px) scale(0); + -o-transform: translate(113.96px, 61.6px) scale(0); + -ms-transform: translate(113.96px, 61.6px) scale(0); + transform: translate(113.96px, 61.6px) scale(0); + } +} +@-o-keyframes loading-ball-r { + 0% { + -webkit-transform: translate(113.96px, 61.6px) scale(1); + -moz-transform: translate(113.96px, 61.6px) scale(1); + -o-transform: translate(113.96px, 61.6px) scale(1); + -ms-transform: translate(113.96px, 61.6px) scale(1); + transform: translate(113.96px, 61.6px) scale(1); + } + 100% { + -webkit-transform: translate(113.96px, 61.6px) scale(0); + -moz-transform: translate(113.96px, 61.6px) scale(0); + -o-transform: translate(113.96px, 61.6px) scale(0); + -ms-transform: translate(113.96px, 61.6px) scale(0); + transform: translate(113.96px, 61.6px) scale(0); + } +} +@keyframes loading-ball-r { + 0% { + -webkit-transform: translate(113.96px, 61.6px) scale(1); + -moz-transform: translate(113.96px, 61.6px) scale(1); + -o-transform: translate(113.96px, 61.6px) scale(1); + -ms-transform: translate(113.96px, 61.6px) scale(1); + transform: translate(113.96px, 61.6px) scale(1); + } + 100% { + -webkit-transform: translate(113.96px, 61.6px) scale(0); + -moz-transform: translate(113.96px, 61.6px) scale(0); + -o-transform: translate(113.96px, 61.6px) scale(0); + -ms-transform: translate(113.96px, 61.6px) scale(0); + transform: translate(113.96px, 61.6px) scale(0); + } +} +@-moz-keyframes loading-ball-c { + 0% { + background: #e15b64; + } + 25% { + background: #abbd81; + } + 50% { + background: #f8b26a; + } + 75% { + background: #f47e60; + } + 100% { + background: #e15b64; + } +} +@-webkit-keyframes loading-ball-c { + 0% { + background: #e15b64; + } + 25% { + background: #abbd81; + } + 50% { + background: #f8b26a; + } + 75% { + background: #f47e60; + } + 100% { + background: #e15b64; + } +} +@-o-keyframes loading-ball-c { + 0% { + background: #e15b64; + } + 25% { + background: #abbd81; + } + 50% { + background: #f8b26a; + } + 75% { + background: #f47e60; + } + 100% { + background: #e15b64; + } +} +@keyframes loading-ball-c { + 0% { + background: #e15b64; + } + 25% { + background: #abbd81; + } + 50% { + background: #f8b26a; + } + 75% { + background: #f47e60; + } + 100% { + background: #e15b64; + } +} +blockquote.pullquote { + position: relative; + max-width: 45%; + font-size: 110%; +} +blockquote.pullquote.left { + float: left; + margin: 1em 0.5em 0 0; +} +blockquote.pullquote.right { + float: right; + margin: 1em 0 0 0.5em; +} +.video-container { + position: relative; + overflow: hidden; + margin-bottom: 16px; + padding-top: 56.25%; + height: 0; +} +.video-container iframe { + position: absolute; + top: 0; + left: 0; + margin-top: 0; + width: 100%; + height: 100%; +} +.hide-inline > .hide-button, +.hide-block > .hide-button { + display: inline-block; + padding: 5px 18px; + background: #49b1f5; + color: var(--white); + border-radius: 6px; +} +.hide-inline > .hide-button:hover, +.hide-block > .hide-button:hover { + background-color: var(--btn-hover-color); +} +.hide-inline > .hide-button.open, +.hide-block > .hide-button.open { + display: none; +} +.hide-inline > .hide-button.open + div, +.hide-block > .hide-button.open + div { + display: block; +} +.hide-inline > .hide-button.open + span, +.hide-block > .hide-button.open + span { + display: inline; +} +.hide-inline > .hide-content, +.hide-block > .hide-content { + display: none; +} +.hide-inline > .hide-button { + margin: 0 6px; +} +.hide-inline > .hide-content { + margin: 0 6px; +} +.hide-block { + margin: 0 0 16px; +} +.toggle { + margin-bottom: 20px; + border: 1px solid #f0f0f0; + border-radius: 5px; + overflow: hidden; +} +.toggle > .toggle-button { + padding: 6px 15px; + background: #f0f0f0; + color: #1f2d3d; + cursor: pointer; +} +.toggle > .toggle-content { + margin: 30px 24px; +} +.container .inline-img { + display: inline; + margin: 0 3px; + height: 1.1em; + vertical-align: text-bottom; +} +.hl-label { + padding: 2px 4px; + color: #fff; + border-radius: 3px; +} +.hl-label.default { + background-color: #777; +} +.hl-label.blue { + background-color: #428bca; +} +.hl-label.pink { + background-color: #ff69b4; +} +.hl-label.red { + background-color: #f00; +} +.hl-label.purple { + background-color: #6f42c1; +} +.hl-label.orange { + background-color: #ff8c00; +} +.hl-label.green { + background-color: #5cb85c; +} +.note { + position: relative; + margin: 0 0 20px; + padding: 15px; + border-radius: 3px; +} +.note.icon-padding { + padding-left: 3em; +} +.note > .note-icon { + position: absolute; + top: calc(50% - 0.5em); + left: 0.8em; + font-size: larger; +} +.note.blue:not(.disabled) { + border-left-color: #428bca !important; +} +.note.blue:not(.disabled).modern { + border-left-color: transparent !important; + color: #428bca; +} +.note.blue:not(.disabled):not(.simple) { + background: #e3eef7 !important; +} +.note.blue > .note-icon { + color: #428bca; +} +.note.pink:not(.disabled) { + border-left-color: #ff69b4 !important; +} +.note.pink:not(.disabled).modern { + border-left-color: transparent !important; + color: #ff69b4; +} +.note.pink:not(.disabled):not(.simple) { + background: #ffe9f4 !important; +} +.note.pink > .note-icon { + color: #ff69b4; +} +.note.red:not(.disabled) { + border-left-color: #f00 !important; +} +.note.red:not(.disabled).modern { + border-left-color: transparent !important; + color: #f00; +} +.note.red:not(.disabled):not(.simple) { + background: #ffd9d9 !important; +} +.note.red > .note-icon { + color: #f00; +} +.note.purple:not(.disabled) { + border-left-color: #6f42c1 !important; +} +.note.purple:not(.disabled).modern { + border-left-color: transparent !important; + color: #6f42c1; +} +.note.purple:not(.disabled):not(.simple) { + background: #e9e3f6 !important; +} +.note.purple > .note-icon { + color: #6f42c1; +} +.note.orange:not(.disabled) { + border-left-color: #ff8c00 !important; +} +.note.orange:not(.disabled).modern { + border-left-color: transparent !important; + color: #ff8c00; +} +.note.orange:not(.disabled):not(.simple) { + background: #ffeed9 !important; +} +.note.orange > .note-icon { + color: #ff8c00; +} +.note.green:not(.disabled) { + border-left-color: #5cb85c !important; +} +.note.green:not(.disabled).modern { + border-left-color: transparent !important; + color: #5cb85c; +} +.note.green:not(.disabled):not(.simple) { + background: #e7f4e7 !important; +} +.note.green > .note-icon { + color: #5cb85c; +} +.note.simple { + border: 1px solid #eee; + border-left-width: 5px; +} +.note.modern { + border: 1px solid transparent !important; + background-color: #f5f5f5; + color: #4c4948; +} +.note.flat { + border: initial; + border-left: 5px solid #eee; + background-color: #f9f9f9; + color: #4c4948; +} +.note h2, +.note h3, +.note h4, +.note h5, +.note h6 { + margin-top: 3px; + margin-bottom: 0; + padding-top: 0 !important; + border-bottom: initial; +} +.note p:first-child, +.note ul:first-child, +.note ol:first-child, +.note table:first-child, +.note pre:first-child, +.note blockquote:first-child, +.note img:first-child { + margin-top: 0 !important; +} +.note p:last-child, +.note ul:last-child, +.note ol:last-child, +.note table:last-child, +.note pre:last-child, +.note blockquote:last-child, +.note img:last-child { + margin-bottom: 0 !important; +} +.note .img-alt { + margin: 5px 0 10px; +} +.note:not(.no-icon) { + padding-left: 3em; +} +.note:not(.no-icon)::before { + position: absolute; + top: calc(50% - 0.95em); + left: 0.8em; + font-size: larger; +} +.note.default.flat { + background: #f7f7f7; +} +.note.default.modern { + border-color: #e1e1e1; + background: #f3f3f3; + color: #666; +} +.note.default.modern a:not(.btn) { + color: #666; +} +.note.default.modern a:not(.btn):hover { + color: #454545; +} +.note.default:not(.modern) { + border-left-color: #777; +} +.note.default:not(.modern) h2, +.note.default:not(.modern) h3, +.note.default:not(.modern) h4, +.note.default:not(.modern) h5, +.note.default:not(.modern) h6 { + color: #777; +} +.note.default:not(.no-icon)::before { + content: '\f0a9'; +} +.note.default:not(.no-icon):not(.modern)::before { + color: #777; +} +.note.primary.flat { + background: #f5f0fa; +} +.note.primary.modern { + border-color: #e1c2ff; + background: #f3daff; + color: #6f42c1; +} +.note.primary.modern a:not(.btn) { + color: #6f42c1; +} +.note.primary.modern a:not(.btn):hover { + color: #453298; +} +.note.primary:not(.modern) { + border-left-color: #6f42c1; +} +.note.primary:not(.modern) h2, +.note.primary:not(.modern) h3, +.note.primary:not(.modern) h4, +.note.primary:not(.modern) h5, +.note.primary:not(.modern) h6 { + color: #6f42c1; +} +.note.primary:not(.no-icon)::before { + content: '\f055'; +} +.note.primary:not(.no-icon):not(.modern)::before { + color: #6f42c1; +} +.note.info.flat { + background: #eef7fa; +} +.note.info.modern { + border-color: #b3e5ef; + background: #d9edf7; + color: #31708f; +} +.note.info.modern a:not(.btn) { + color: #31708f; +} +.note.info.modern a:not(.btn):hover { + color: #215761; +} +.note.info:not(.modern) { + border-left-color: #428bca; +} +.note.info:not(.modern) h2, +.note.info:not(.modern) h3, +.note.info:not(.modern) h4, +.note.info:not(.modern) h5, +.note.info:not(.modern) h6 { + color: #428bca; +} +.note.info:not(.no-icon)::before { + content: '\f05a'; +} +.note.info:not(.no-icon):not(.modern)::before { + color: #428bca; +} +.note.success.flat { + background: #eff8f0; +} +.note.success.modern { + border-color: #d0e6be; + background: #dff0d8; + color: #3c763d; +} +.note.success.modern a:not(.btn) { + color: #3c763d; +} +.note.success.modern a:not(.btn):hover { + color: #32562c; +} +.note.success:not(.modern) { + border-left-color: #5cb85c; +} +.note.success:not(.modern) h2, +.note.success:not(.modern) h3, +.note.success:not(.modern) h4, +.note.success:not(.modern) h5, +.note.success:not(.modern) h6 { + color: #5cb85c; +} +.note.success:not(.no-icon)::before { + content: '\f058'; +} +.note.success:not(.no-icon):not(.modern)::before { + color: #5cb85c; +} +.note.warning.flat { + background: #fdf8ea; +} +.note.warning.modern { + border-color: #fae4cd; + background: #fcf4e3; + color: #8a6d3b; +} +.note.warning.modern a:not(.btn) { + color: #8a6d3b; +} +.note.warning.modern a:not(.btn):hover { + color: #714f30; +} +.note.warning:not(.modern) { + border-left-color: #f0ad4e; +} +.note.warning:not(.modern) h2, +.note.warning:not(.modern) h3, +.note.warning:not(.modern) h4, +.note.warning:not(.modern) h5, +.note.warning:not(.modern) h6 { + color: #f0ad4e; +} +.note.warning:not(.no-icon)::before { + content: '\f06a'; +} +.note.warning:not(.no-icon):not(.modern)::before { + color: #f0ad4e; +} +.note.danger.flat { + background: #fcf1f2; +} +.note.danger.modern { + border-color: #ebcdd2; + background: #f2dfdf; + color: #a94442; +} +.note.danger.modern a:not(.btn) { + color: #a94442; +} +.note.danger.modern a:not(.btn):hover { + color: #84333f; +} +.note.danger:not(.modern) { + border-left-color: #d9534f; +} +.note.danger:not(.modern) h2, +.note.danger:not(.modern) h3, +.note.danger:not(.modern) h4, +.note.danger:not(.modern) h5, +.note.danger:not(.modern) h6 { + color: #d9534f; +} +.note.danger:not(.no-icon)::before { + content: '\f056'; +} +.note.danger:not(.no-icon):not(.modern)::before { + color: #d9534f; +} +.container .series-items a:hover { + color: var(--pseudo-hover); +} +.container .tabs { + position: relative; + margin: 0 0 20px; + border-right: 1px solid var(--tab-border-color); + border-bottom: 1px solid var(--tab-border-color); + border-left: 1px solid var(--tab-border-color); + border-radius: 6px; + overflow: hidden; +} +.container .tabs > .nav-tabs { + display: -webkit-box; + display: -moz-box; + display: -webkit-flex; + display: -ms-flexbox; + display: box; + display: flex; + -webkit-box-lines: multiple; + -moz-box-lines: multiple; + -o-box-lines: multiple; + -webkit-flex-wrap: wrap; + -ms-flex-wrap: wrap; + flex-wrap: wrap; + margin: 0; + padding: 0; + background: var(--tab-botton-bg); +} +.container .tabs > .nav-tabs > .tab { + -webkit-box-flex: 1; + -moz-box-flex: 1; + -o-box-flex: 1; + -ms-box-flex: 1; + box-flex: 1; + -webkit-flex-grow: 1; + flex-grow: 1; + padding: 8px 18px; + border-top: 2px solid var(--tab-border-color); + background: var(--tab-botton-bg); + color: var(--tab-botton-color); + line-height: 2; + -webkit-transition: all 0.4s; + -moz-transition: all 0.4s; + -o-transition: all 0.4s; + -ms-transition: all 0.4s; + transition: all 0.4s; +} +.container .tabs > .nav-tabs > .tab i { + width: 1.5em; +} +.container .tabs > .nav-tabs > .tab.active { + border-top: 2px solid #49b1f5; + background: var(--tab-button-active-bg); + cursor: default; +} +.container .tabs > .nav-tabs > .tab:not(.active):hover { + border-top: 2px solid var(--tab-button-hover-bg); + background: var(--tab-button-hover-bg); +} +.container .tabs > .nav-tabs.no-default ~ .tab-to-top { + display: none; +} +.container .tabs > .tab-contents .tab-item-content { + position: relative; + display: none; + padding: 36px 24px 10px; +} +@media screen and (max-width: 768px) { + .container .tabs > .tab-contents .tab-item-content { + padding: 24px 14px; + } +} +.container .tabs > .tab-contents .tab-item-content.active { + display: block; + -webkit-animation: tabshow 0.5s; + -moz-animation: tabshow 0.5s; + -o-animation: tabshow 0.5s; + -ms-animation: tabshow 0.5s; + animation: tabshow 0.5s; +} +.container .tabs > .tab-contents .tab-item-content > :last-child { + margin-bottom: 0; +} +.container .tabs > .tab-to-top { + padding: 0 16px 10px 0; + width: 100%; + text-align: right; +} +.container .tabs > .tab-to-top button { + color: #99a9bf; +} +.container .tabs > .tab-to-top button:hover { + color: #49b1f5; +} +@-moz-keyframes tabshow { + 0% { + -webkit-transform: translateY(15px); + -moz-transform: translateY(15px); + -o-transform: translateY(15px); + -ms-transform: translateY(15px); + transform: translateY(15px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-webkit-keyframes tabshow { + 0% { + -webkit-transform: translateY(15px); + -moz-transform: translateY(15px); + -o-transform: translateY(15px); + -ms-transform: translateY(15px); + transform: translateY(15px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@-o-keyframes tabshow { + 0% { + -webkit-transform: translateY(15px); + -moz-transform: translateY(15px); + -o-transform: translateY(15px); + -ms-transform: translateY(15px); + transform: translateY(15px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +@keyframes tabshow { + 0% { + -webkit-transform: translateY(15px); + -moz-transform: translateY(15px); + -o-transform: translateY(15px); + -ms-transform: translateY(15px); + transform: translateY(15px); + } + 100% { + -webkit-transform: translateY(0); + -moz-transform: translateY(0); + -o-transform: translateY(0); + -ms-transform: translateY(0); + transform: translateY(0); + } +} +.container .timeline { + margin: 0 10px 20px; + padding: 14px 0 5px 20px; + border-left: 2px solid var(--timeline-color, #49b1f5); +} +.container .timeline.blue { + --timeline-color: #428bca; + --timeline-bg: rgba(66,139,202, 0.2); +} +.container .timeline.pink { + --timeline-color: #ff69b4; + --timeline-bg: rgba(255,105,180, 0.2); +} +.container .timeline.red { + --timeline-color: #f00; + --timeline-bg: rgba(255,0,0, 0.2); +} +.container .timeline.purple { + --timeline-color: #6f42c1; + --timeline-bg: rgba(111,66,193, 0.2); +} +.container .timeline.orange { + --timeline-color: #ff8c00; + --timeline-bg: rgba(255,140,0, 0.2); +} +.container .timeline.green { + --timeline-color: #5cb85c; + --timeline-bg: rgba(92,184,92, 0.2); +} +.container .timeline .timeline-item { + margin: 0 0 15px; +} +.container .timeline .timeline-item:hover .item-circle:before { + border-color: var(--timeline-color, #49b1f5); +} +.container .timeline .timeline-item.headline .timeline-item-title .item-circle > p { + font-weight: 600; + font-size: 1.2em; +} +.container .timeline .timeline-item.headline .timeline-item-title .item-circle:before { + left: -28px; + border: 4px solid var(--timeline-color, #49b1f5); +} +.container .timeline .timeline-item.headline:hover .item-circle:before { + border-color: var(--pseudo-hover); +} +.container .timeline .timeline-item .timeline-item-title { + position: relative; +} +.container .timeline .timeline-item .item-circle:before { + position: absolute; + top: 50%; + left: -27px; + width: 6px; + height: 6px; + border: 3px solid var(--pseudo-hover); + border-radius: 50%; + background: var(--card-bg); + content: ''; + -webkit-transition: all 0.3s; + -moz-transition: all 0.3s; + -o-transition: all 0.3s; + -ms-transition: all 0.3s; + transition: all 0.3s; + -webkit-transform: translate(0, -50%); + -moz-transform: translate(0, -50%); + -o-transform: translate(0, -50%); + -ms-transform: translate(0, -50%); + transform: translate(0, -50%); +} +.container .timeline .timeline-item .item-circle > p { + margin: 0 0 8px; + font-weight: 500; +} +.container .timeline .timeline-item .timeline-item-content { + position: relative; + padding: 12px 15px; + border-radius: 8px; + background: var(--timeline-bg, #e4f3fd); + font-size: 0.93em; +} +.container .timeline .timeline-item .timeline-item-content > :last-child { + margin-bottom: 0; +} +.container .timeline + .timeline { + margin-top: -20px; +} +[data-theme='dark'] { + --global-bg: #0d0d0d; + --font-color: rgba(255,255,255,0.7); + --hr-border: rgba(255,255,255,0.4); + --hr-before-color: rgba(255,255,255,0.7); + --search-bg: #121212; + --search-input-color: rgba(255,255,255,0.7); + --search-a-color: rgba(255,255,255,0.7); + --preloader-bg: #0d0d0d; + --preloader-color: rgba(255,255,255,0.7); + --tab-border-color: #2c2c2c; + --tab-botton-bg: #2c2c2c; + --tab-botton-color: rgba(255,255,255,0.7); + --tab-button-hover-bg: #383838; + --tab-button-active-bg: #121212; + --card-bg: #121212; + --sidebar-bg: #121212; + --sidebar-menu-bg: #1f1f1f; + --btn-hover-color: #787878; + --btn-color: rgba(255,255,255,0.7); + --btn-bg: #1f1f1f; + --text-bg-hover: #383838; + --light-grey: rgba(255,255,255,0.7); + --dark-grey: rgba(255,255,255,0.2); + --white: rgba(255,255,255,0.9); + --text-highlight-color: rgba(255,255,255,0.9); + --blockquote-color: rgba(255,255,255,0.7); + --blockquote-bg: #2c2c2c; + --reward-pop: #2c2c2c; + --toc-link-color: rgba(255,255,255,0.6); + --scrollbar-color: #525252; + --timeline-bg: #1f1f1f; + --zoom-bg: #121212; + --mark-bg: rgba(0,0,0,0.6); +} +[data-theme='dark'] #web_bg:before { + position: absolute; + width: 100%; + height: 100%; + background-color: rgba(0,0,0,0.7); + content: ''; +} +[data-theme='dark'] .container code { + background: #2c2c2c; +} +[data-theme='dark'] .container pre > code { + background: #171717; +} +[data-theme='dark'] .container figure.highlight { + -webkit-box-shadow: none; + box-shadow: none; +} +[data-theme='dark'] .container .note code { + background: rgba(27,31,35,0.05); +} +[data-theme='dark'] .container .aplayer { + filter: brightness(0.8); +} +[data-theme='dark'] .container kbd { + border-color: #696969; + background-color: #525252; + color: #e2f1ff; +} +[data-theme='dark'] #page-header.nav-fixed > #nav, +[data-theme='dark'] #page-header.not-top-img > #nav { + background: rgba(18,18,18,0.8); + -webkit-box-shadow: 0 5px 6px -5px rgba(133,133,133,0); + box-shadow: 0 5px 6px -5px rgba(133,133,133,0); +} +[data-theme='dark'] #post-comment .comment-switch { + background: #2c2c2c !important; +} +[data-theme='dark'] #post-comment .comment-switch #switch-btn { + filter: brightness(0.8); +} +[data-theme='dark'] .note { + filter: brightness(0.8); +} +[data-theme='dark'] .hide-button, +[data-theme='dark'] .btn-beautify, +[data-theme='dark'] .hl-label, +[data-theme='dark'] #post-outdate-notice, +[data-theme='dark'] .error-img, +[data-theme='dark'] .container iframe, +[data-theme='dark'] .gist, +[data-theme='dark'] .ads-wrap { + filter: brightness(0.8); +} +[data-theme='dark'] img { + filter: brightness(0.8); +} +[data-theme='dark'] #aside-content .aside-list > .aside-list-item:not(:last-child) { + border-bottom: 1px dashed rgba(255,255,255,0.1); +} +[data-theme='dark'] #gitalk-container { + filter: brightness(0.8); +} +[data-theme='dark'] #gitalk-container svg { + fill: rgba(255,255,255,0.9) !important; +} +[data-theme='dark'] #disqusjs #dsqjs:hover, +[data-theme='dark'] #disqusjs #dsqjs:focus, +[data-theme='dark'] #disqusjs #dsqjs .dsqjs-tab-active, +[data-theme='dark'] #disqusjs #dsqjs .dsqjs-no-comment { + color: rgba(255,255,255,0.7); +} +[data-theme='dark'] #disqusjs #dsqjs .dsqjs-order-label { + background-color: #1f1f1f; +} +[data-theme='dark'] #disqusjs #dsqjs .dsqjs-post-body { + color: rgba(255,255,255,0.7); +} +[data-theme='dark'] #disqusjs #dsqjs .dsqjs-post-body code, +[data-theme='dark'] #disqusjs #dsqjs .dsqjs-post-body pre { + background: #2c2c2c; +} +[data-theme='dark'] #disqusjs #dsqjs .dsqjs-post-body blockquote { + color: rgba(255,255,255,0.7); +} +[data-theme='dark'] #artitalk_main #lazy { + background: #121212; +} +[data-theme='dark'] #operare_artitalk .c2 { + background: #121212; +} +@media screen and (max-width: 900px) { + [data-theme='dark'] #card-toc { + background: #1f1f1f; + } +} +[data-theme='dark'] .artalk.atk-dark-mode, +[data-theme='dark'] .atk-layer-wrap.atk-dark-mode { + --at-color-font: rgba(255,255,255,0.7); + --at-color-meta: rgba(255,255,255,0.7); + --at-color-grey: rgba(255,255,255,0.7); +} +[data-theme='dark'] .atk-send-btn, +[data-theme='dark'] .atk-badge { + color: rgba(255,255,255,0.7) !important; +} +[data-theme='dark'] #waline-wrap { + --waline-color: rgba(255,255,255,0.7); + --waline-dark-grey: rgba(255,255,255,0.7); + --waline-info-color: rgba(255,255,255,0.5); +} +.read-mode { + --font-color: #4c4948; + --readmode-light-color: #fff; + --white: #4c4948; + --light-grey: #4c4948; + --gray: #d6dbdf; + --hr-border: #d6dbdf; + --hr-before-color: #b9c2c9; + --highlight-bg: #f7f7f7; + --exit-btn-bg: #c0c0c0; + --exit-btn-color: #fff; + --exit-btn-hover: #8d8d8d; + --pseudo-hover: none; +} +[data-theme='dark'] .read-mode { + --font-color: rgba(255,255,255,0.7); + --readmode-light-color: #0d0d0d; + --white: rgba(255,255,255,0.9); + --light-grey: rgba(255,255,255,0.7); + --gray: rgba(255,255,255,0.7); + --hr-border: rgba(255,255,255,0.5); + --hr-before-color: rgba(255,255,255,0.7); + --highlight-bg: #171717; + --exit-btn-bg: #1f1f1f; + --exit-btn-color: rgba(255,255,255,0.9); + --exit-btn-hover: #525252; +} +.read-mode { + background: var(--readmode-light-color); +} +.read-mode .exit-readmode { + position: fixed; + top: 30px; + right: 30px; + z-index: 100; + width: 40px; + height: 40px; + background: var(--exit-btn-bg); + color: var(--exit-btn-color); + font-size: 16px; + -webkit-transition: background 0.3s; + -moz-transition: background 0.3s; + -o-transition: background 0.3s; + -ms-transition: background 0.3s; + transition: background 0.3s; + border-radius: 8px; +} +@media screen and (max-width: 768px) { + .read-mode .exit-readmode { + top: initial; + bottom: 30px; + } +} +.read-mode .exit-readmode:hover { + background: var(--exit-btn-hover); +} +.read-mode #aside-content { + display: none; +} +.read-mode #page-header.post-bg { + background: none !important; +} +.read-mode #page-header.post-bg:before { + opacity: 0; + -ms-filter: "progid:DXImageTransform.Microsoft.Alpha(Opacity=0)"; + filter: alpha(opacity=0); +} +.read-mode #page-header.post-bg > #post-info { + text-align: center; +} +.read-mode #post { + margin: 0 auto; + background: transparent; + -webkit-box-shadow: none; + box-shadow: none; +} +.read-mode #post:hover { + -webkit-box-shadow: none; + box-shadow: none; +} +.read-mode > canvas { + display: none !important; +} +.read-mode .highlight-tools, +.read-mode #footer, +.read-mode #post > *:not(#post-info):not(.post-content), +.read-mode #nav, +.read-mode #post-outdate-notice, +.read-mode #web_bg, +.read-mode #rightside, +.read-mode .not-top-img { + display: none !important; +} +.read-mode .container a { + color: #99a9bf; +} +.read-mode .container pre, +.read-mode .container .highlight:not(.js-file-line-container) { + background: var(--highlight-bg) !important; +} +.read-mode .container pre *, +.read-mode .container .highlight:not(.js-file-line-container) * { + color: var(--font-color) !important; +} +.read-mode .container figure.highlight { + border-radius: 0 !important; + -webkit-box-shadow: none !important; + box-shadow: none !important; +} +.read-mode .container figure.highlight > :not(.highlight-tools) { + display: block !important; +} +.read-mode .container figure.highlight .line:before { + color: var(--font-color) !important; +} +.read-mode .container figure.highlight .hljs { + background: var(--highlight-bg) !important; +} +.read-mode .container h1, +.read-mode .container h2, +.read-mode .container h3, +.read-mode .container h4, +.read-mode .container h5, +.read-mode .container h6 { + padding: 0; +} +.read-mode .container h1:before, +.read-mode .container h2:before, +.read-mode .container h3:before, +.read-mode .container h4:before, +.read-mode .container h5:before, +.read-mode .container h6:before { + content: ''; +} +.read-mode .container h1:hover, +.read-mode .container h2:hover, +.read-mode .container h3:hover, +.read-mode .container h4:hover, +.read-mode .container h5:hover, +.read-mode .container h6:hover { + padding: 0; +} +.read-mode .container ul:hover:before, +.read-mode .container li:hover:before, +.read-mode .container ol:hover:before { + -webkit-transform: none !important; + -moz-transform: none !important; + -o-transform: none !important; + -ms-transform: none !important; + transform: none !important; +} +.read-mode .container ol:before, +.read-mode .container li:before { + background: transparent !important; + color: var(--font-color) !important; +} +.read-mode .container ul >li:before { + border-color: var(--gray) !important; +} +.read-mode .container .tabs { + border: 2px solid var(--tab-border-color); +} +.read-mode .container .tabs > .nav-tabs { + background: transparent; +} +.read-mode .container .tabs > .nav-tabs > .tab { + border-top: none !important; +} +.read-mode .container .tabs > .tab-contents .tab-item-content.active { + -webkit-animation: none; + -moz-animation: none; + -o-animation: none; + -ms-animation: none; + animation: none; +} +.read-mode .container code { + color: var(--font-color); +} +.read-mode .container blockquote { + border-color: var(--gray); + background-color: var(--readmode-light-color); +} +.read-mode .container kbd { + border: 1px solid var(--gray); + background-color: transparent; + -webkit-box-shadow: none; + box-shadow: none; + color: var(--font-color); +} +.read-mode .container .hide-toggle { + border: 1px solid var(--gray) !important; +} +.read-mode .container .hide-button, +.read-mode .container .btn-beautify, +.read-mode .container .hl-label { + border: 1px solid var(--gray) !important; + background: var(--readmode-light-color) !important; + color: var(--font-color) !important; +} +.read-mode .container .note { + border: 2px solid var(--gray); + border-left-color: var(--gray) !important; + filter: none; + background-color: var(--readmode-light-color) !important; + color: var(--font-color); +} +.read-mode .container .note:before, +.read-mode .container .note .note-icon { + color: var(--font-color); +} +.search-dialog { + position: fixed; + top: 10%; + left: 50%; + z-index: 1001; + display: none; + margin-left: -300px; + padding: 20px; + width: 600px; + background: var(--search-bg); + --search-height: 100vh; + border-radius: 8px; +} +@media screen and (max-width: 768px) { + .search-dialog { + top: 0; + left: 0; + margin: 0; + width: 100%; + height: 100%; + border-radius: 0; + } +} +.search-dialog .search-nav { + margin: 0 0 14px; + color: #49b1f5; + font-size: 1.4em; + line-height: 1; +} +.search-dialog .search-nav .search-dialog-title { + margin-right: 10px; +} +.search-dialog .search-nav .search-close-button { + float: right; + color: #858585; + -webkit-transition: color 0.2s ease-in-out; + -moz-transition: color 0.2s ease-in-out; + -o-transition: color 0.2s ease-in-out; + -ms-transition: color 0.2s ease-in-out; + transition: color 0.2s ease-in-out; +} +.search-dialog .search-nav .search-close-button:hover { + color: #49b1f5; +} +.search-dialog hr { + margin: 15px auto; +} +#search-mask { + position: fixed; + top: 0; + right: 0; + bottom: 0; + left: 0; + z-index: 1000; + display: none; + background: rgba(0,0,0,0.6); +} diff --git a/css/loading.css b/css/loading.css new file mode 100644 index 0000000..4294978 --- /dev/null +++ b/css/loading.css @@ -0,0 +1,72 @@ +.pace { + -webkit-pointer-events: none; + pointer-events: none; + + -webkit-user-select: none; + -moz-user-select: none; + user-select: none; +} + +.pace .pace-activity { + display: block; + position: fixed; + z-index: 2000; + top: 0; + right: 0; + width: 300px; + height: 300px; + background: #005a8f; + -webkit-transition: -webkit-transform 0.3s; + transition: transform 0.3s; + -webkit-transform: translateX(100%) translateY(-100%) rotate(45deg); + transform: translateX(100%) translateY(-100%) rotate(45deg); + pointer-events: none; +} + +.pace.pace-active .pace-activity { + -webkit-transform: translateX(50%) translateY(-50%) rotate(45deg); + transform: translateX(50%) translateY(-50%) rotate(45deg); +} + +.pace .pace-activity::before, +.pace .pace-activity::after { + -moz-box-sizing: border-box; + box-sizing: border-box; + position: absolute; + bottom: 30px; + left: 50%; + display: block; + border: 5px solid #fff; + border-radius: 50%; + content: ''; +} + +.pace .pace-activity::before { + margin-left: -40px; + width: 80px; + height: 80px; + border-right-color: rgba(0, 0, 0, .2); + border-left-color: rgba(0, 0, 0, .2); + -webkit-animation: pace-theme-corner-indicator-spin 3s linear infinite; + animation: pace-theme-corner-indicator-spin 3s linear infinite; +} + +.pace .pace-activity::after { + bottom: 50px; + margin-left: -20px; + width: 40px; + height: 40px; + border-top-color: rgba(0, 0, 0, .2); + border-bottom-color: rgba(0, 0, 0, .2); + -webkit-animation: pace-theme-corner-indicator-spin 1s linear infinite; + animation: pace-theme-corner-indicator-spin 1s linear infinite; +} + +@-webkit-keyframes pace-theme-corner-indicator-spin { + 0% { -webkit-transform: rotate(0deg); } + 100% { -webkit-transform: rotate(359deg); } +} +@keyframes pace-theme-corner-indicator-spin { + 0% { transform: rotate(0deg); } + 100% { transform: rotate(359deg); } +} \ No newline at end of file diff --git a/placeholder b/css/var.css similarity index 100% rename from placeholder rename to css/var.css diff --git a/img/404.jpg b/img/404.jpg new file mode 100644 index 0000000..4bab3c3 Binary files /dev/null and b/img/404.jpg differ diff --git a/img/avatar.png b/img/avatar.png new file mode 100644 index 0000000..eb1f9b1 Binary files /dev/null and b/img/avatar.png differ diff --git a/img/butterfly-icon.png b/img/butterfly-icon.png new file mode 100644 index 0000000..3992d77 Binary files /dev/null and b/img/butterfly-icon.png differ diff --git a/img/error-page.png b/img/error-page.png new file mode 100644 index 0000000..9d1de96 Binary files /dev/null and b/img/error-page.png differ diff --git a/img/favicon.ico b/img/favicon.ico new file mode 100644 index 0000000..56d07f5 Binary files /dev/null and b/img/favicon.ico differ diff --git a/img/friend_404.gif b/img/friend_404.gif new file mode 100644 index 0000000..91dd56a Binary files /dev/null and b/img/friend_404.gif differ diff --git a/img/link-avatar/ajssad.png b/img/link-avatar/ajssad.png new file mode 100644 index 0000000..986ab41 Binary files /dev/null and b/img/link-avatar/ajssad.png differ diff --git a/img/link-avatar/murasaki.jpg b/img/link-avatar/murasaki.jpg new file mode 100644 index 0000000..f28042c Binary files /dev/null and b/img/link-avatar/murasaki.jpg differ diff --git a/img/link-avatar/rosist.jpg b/img/link-avatar/rosist.jpg new file mode 100644 index 0000000..a98039f Binary files /dev/null and b/img/link-avatar/rosist.jpg differ diff --git a/img/link-avatar/swl.png b/img/link-avatar/swl.png new file mode 100644 index 0000000..fb0a0c1 Binary files /dev/null and b/img/link-avatar/swl.png differ diff --git a/img/link-avatar/yangty.jpg b/img/link-avatar/yangty.jpg new file mode 100644 index 0000000..78ce0ea Binary files /dev/null and b/img/link-avatar/yangty.jpg differ diff --git a/img/swl.png b/img/swl.png new file mode 100644 index 0000000..fb0a0c1 Binary files /dev/null and b/img/swl.png differ diff --git a/img/top.jpg b/img/top.jpg new file mode 100644 index 0000000..9e0ae18 Binary files /dev/null and b/img/top.jpg differ diff --git a/index.html b/index.html new file mode 100644 index 0000000..93f15ec --- /dev/null +++ b/index.html @@ -0,0 +1,238 @@ +正在施工中 - 而那未曾谋面的故事还在继续 + + + + + + + +

正在施工中

电子电路与系统基础（2）：（四）正反馈和负阻
Created
运放正反馈 这个实验做了很多，理解应该是比较深刻了的 正反馈存在解可能非唯一的问题。 在蓝色虚线区工作是不稳定的，物理上无法测出该区域，所以测量得到的是滞回曲线 正反馈和负反馈同时添加（通过负反馈让电路呆在线性区） 显然有1>F，负反馈占优，虚短虚断得到vOUT=0。 在线性区的时候，用加流求压求端口电阻得到负电阻（不能用加压求流） 有一定的约束 在饱和区的时候 同样加流求压，能够得到限制条件，以及电路抽象为戴维南源 看输入输出电压关系，每个电流都有唯一对应电压，认为是流控器件，测量的时候只能加测试电流。这里负反馈大于正反馈 加压的时候正反馈大于负反馈，运放呆不在线性区， 电子系你妈死了
数理方程（4）：位势方程和Green函数法
Created
方程形式 位势方程主要是说 −Δu=f-\Delta u=f −Δu=f 其中Δ=∑i=1d∂2∂xi2\Delta = \sum^{d}_{i=1} \frac{\partial^2}{\partial x_{i}^2}Δ=∑i=1d​∂xi2​∂2​是Laplace算子，d为空间维数，f是源项，当f=0的时候方程又被称为Laplace方程或者调和方程。 Green公式和基本解 Green公式是说： 证明：由于 uΔv=u(∇⋅∇v)=∇⋅(u∇v)−∇u⋅∇vu \Delta v = u(\nabla \cdot \nabla v) = \nabla \cdot(u \nabla v) - \nabla u \cdot \nabla v uΔv=u(∇⋅∇v)=∇⋅(u∇v)−∇u⋅∇v （直接拆开就能得到） 所以有 uΔv−vΔu=∇⋅(u∇v−v∇u)u \Delta v - v \Delta u = \nabla \cdot(u \nabla v - v \nabla...
数理方程（五）分离变量法
Created
终于讲到大杀器了，为什么不早点讲啊
电子电路与系统基础（2）：（三）负反馈网络
Created
...
数理方程（3）：热传导方程和积分变换初步
Created
一维初值问题 解方程 考虑一维热传导方程初值问题 ∂tu−a2∂xxu=f(x,t)u(x,0)=φ(x)\partial_{t} u - a^2\partial_{x x}u = f(x,t)\\ u(x,0) = \varphi (x) ∂t​u−a2∂xx​u=f(x,t)u(x,0)=φ(x) 对u，在x上做傅立叶变换 u(x,t)→Fu^(x,t),∂xxu^=(iω)2u^u(x,t) \stackrel{\mathcal{F}}{\rightarrow} \hat{u}(x,t), \partial_{x x}\hat{u} = (i \omega)^2\hat{u} u(x,t)→Fu^(x,t),∂xx​u^=(iω)2u^ 那么偏微分方程被我们转换成为了 ∂tu^+a2ω2u^=f^(ω,t)u^(x,0)=φ^(x)\partial_{t} \hat{u} + a^2 \omega^2 \hat{u} = \hat{f}(\omega,t)\\ \hat{u}(x,0) =...
数理方程（二）波动方程的延续
Created
D’Alembert公式的解释 先复习一下D’Alembert公式 u(x,t)=12(φ(x+at)+φ(x−at))+12a∫x−atx+atψ(ξ)dξu(x,t) = \frac{1}{2}(\varphi(x+at)+\varphi(x-at))+\frac{1}{2a}\int^{x+at}_{x-at}\psi(\xi)\rm d...
电子电路与系统基础（2）：频率特性
Created
...
电子电路与系统基础（2）：（二）大信号放大器
Created
高增益放大器 最初步的肯定是我们之前学过的小信号放大器。 将晶体管反相器偏置在工作电压处，提供极大的交流电阻，以获得高电压增益。能够实现Av0=−gm(rds1∥rds2)A_{v_0}= -g_m(r_{ds1}\parallel...
数理方程学习笔记（一）：波动方程初步
Created
特征线法 常系数运输方程初值问题 对于方程 ∂tρ+a∂xρ=0,x∈R,t>0\partial_t \rho + a \partial_x \rho = 0, x \in \mathbb{R}, t > 0 ∂t​ρ+a∂x​ρ=0,x∈R,t>0 给定初值条件 ρ(x,0)=ρ0(x)\rho(x,0) = \rho_0(x) ρ(x,0)=ρ0​(x) 我们发现在特征线上，ρ\rhoρ 保持不变，然后通过特征线反推每一点ρ\rhoρ的值 具体而言是这样的，特征线是下面的常微分方程初值问题的解 dxdt=a,x(0)=x0\frac{\rm{d}x}{\rm{d}t} = a, x(0) = x_0 dtdx​=a,x(0)=x0​ 其实这条线就是x(t,x0)=at+x0x(t,x_0) = at + x_0x(t,x0​)=at+x0​，但是写成微分形式其实是为了下面的推导 根据全微分公式 df=∂f∂xdx+∂f∂tdt\rm{d}f = \frac{\partial f}{\partial x} \rm{d}x + \frac{\partial...
电子电路与系统基础复习（1）二端口网络参量：一切故事的开始
Created
网络参量的引入 对于一个电路系统来说，最朴素的认知是认为系统分别有输入输出两个端口，因此对二端口网络的描述是最为重要并且基础的。 我们所能直接测量的无非网络的电流和电压，两个端口也就是两组电流和电压，对于线性网络来说，我们很容易能够列出来四个变量组成的二元一次方程组 比如对如图所示的二端口网络，我们可以列出如下的方程组 v1=(R1+R2)i1+R2i2v2=R2i1+R2i2v_1 = (R_1+R_2)i_1 + R_2i_2 \\\\ v_2 = R_2i_1 + R_2i_2 v1​=(R1​+R2​)i1​+R2​i2​v2​=R2​i1​+R2​i2​ 矩阵形式也就是 [v1v2]=[R1+R2R2R2R2][i1i2]\begin{gathered} \begin{bmatrix} v_1 \\\\ v_2 \end{bmatrix} = \begin{bmatrix} R_1+R_2 & R_2 \\\\ R_2 & R_2 \end{bmatrix} \begin{bmatrix} i_1 \\\\ i_2...
avatar
zirno81
Articles
12
Tags
0
Categories
0
Follow Me
Announcement
This is my Blog
Recent Posts
电子电路与系统基础（2）：（四）正反馈和负阻
数理方程（4）：位势方程和Green函数法
数理方程（五）分离变量法
电子电路与系统基础（2）：（三）负反馈网络
数理方程（3）：热传导方程和积分变换初步
+
+ + Archives + +
+
Website Info
Article Count :
12
Last Update :
\ No newline at end of file diff --git a/js/main.js b/js/main.js new file mode 100644 index 0000000..42cfd97 --- /dev/null +++ b/js/main.js @@ -0,0 +1,923 @@ +document.addEventListener('DOMContentLoaded', () => { + let headerContentWidth, $nav + let mobileSidebarOpen = false + + const adjustMenu = init => { + const getAllWidth = ele => Array.from(ele).reduce((width, i) => width + i.offsetWidth, 0) + + if (init) { + const blogInfoWidth = getAllWidth(document.querySelector('#blog-info > a').children) + const menusWidth = getAllWidth(document.getElementById('menus').children) + headerContentWidth = blogInfoWidth + menusWidth + $nav = document.getElementById('nav') + } + + const hideMenuIndex = window.innerWidth <= 768 || headerContentWidth > $nav.offsetWidth - 120 + $nav.classList.toggle('hide-menu', hideMenuIndex) + } + + // 初始化header + const initAdjust = () => { + adjustMenu(true) + $nav.classList.add('show') + } + + // sidebar menus + const sidebarFn = { + open: () => { + btf.overflowPaddingR.add() + btf.animateIn(document.getElementById('menu-mask'), 'to_show 0.5s') + document.getElementById('sidebar-menus').classList.add('open') + mobileSidebarOpen = true + }, + close: () => { + btf.overflowPaddingR.remove() + btf.animateOut(document.getElementById('menu-mask'), 'to_hide 0.5s') + document.getElementById('sidebar-menus').classList.remove('open') + mobileSidebarOpen = false + } + } + + /** + * 首頁top_img底下的箭頭 + */ + const scrollDownInIndex = () => { + const handleScrollToDest = () => { + btf.scrollToDest(document.getElementById('content-inner').offsetTop, 300) + } + + const $scrollDownEle = document.getElementById('scroll-down') + $scrollDownEle && btf.addEventListenerPjax($scrollDownEle, 'click', handleScrollToDest) + } + + /** + * 代碼 + * 只適用於Hexo默認的代碼渲染 + */ + const addHighlightTool = () => { + const highLight = GLOBAL_CONFIG.highlight + if (!highLight) return + + const { highlightCopy, highlightLang, highlightHeightLimit, highlightFullpage, highlightMacStyle, plugin } = highLight + const isHighlightShrink = GLOBAL_CONFIG_SITE.isHighlightShrink + const isShowTool = highlightCopy || highlightLang || isHighlightShrink !== undefined || highlightFullpage || highlightMacStyle + const $figureHighlight = plugin === 'highlight.js' ? document.querySelectorAll('figure.highlight') : document.querySelectorAll('pre[class*="language-"]') + + if (!((isShowTool || highlightHeightLimit) && $figureHighlight.length)) return + + const isPrismjs = plugin === 'prismjs' + const highlightShrinkClass = isHighlightShrink === true ? 'closed' : '' + const highlightShrinkEle = isHighlightShrink !== undefined ? '' : '' + const highlightCopyEle = highlightCopy ? '
' : '' + const highlightMacStyleEle = '
' + const highlightFullpageEle = highlightFullpage ? '' : '' + + const alertInfo = (ele, text) => { + if (GLOBAL_CONFIG.Snackbar !== undefined) { + btf.snackbarShow(text) + } else { + ele.textContent = text + ele.style.opacity = 1 + setTimeout(() => { ele.style.opacity = 0 }, 800) + } + } + + const copy = async (text, ctx) => { + try { + await navigator.clipboard.writeText(text) + alertInfo(ctx, GLOBAL_CONFIG.copy.success) + } catch (err) { + console.error('Failed to copy: ', err) + alertInfo(ctx, GLOBAL_CONFIG.copy.noSupport) + } + } + + // click events + const highlightCopyFn = (ele, clickEle) => { + const $buttonParent = ele.parentNode + $buttonParent.classList.add('copy-true') + const preCodeSelector = isPrismjs ? 'pre code' : 'table .code pre' + const codeElement = $buttonParent.querySelector(preCodeSelector) + if (!codeElement) return + copy(codeElement.innerText, clickEle.previousElementSibling) + $buttonParent.classList.remove('copy-true') + } + + const highlightShrinkFn = ele => ele.classList.toggle('closed') + + const codeFullpage = (item, clickEle) => { + const wrapEle = item.closest('figure.highlight') + const isFullpage = wrapEle.classList.toggle('code-fullpage') + + document.body.style.overflow = isFullpage ? 'hidden' : '' + clickEle.classList.toggle('fa-down-left-and-up-right-to-center', isFullpage) + clickEle.classList.toggle('fa-up-right-and-down-left-from-center', !isFullpage) + } + + const highlightToolsFn = e => { + const $target = e.target.classList + const currentElement = e.currentTarget + if ($target.contains('expand')) highlightShrinkFn(currentElement) + else if ($target.contains('copy-button')) highlightCopyFn(currentElement, e.target) + else if ($target.contains('fullpage-button')) codeFullpage(currentElement, e.target) + } + + const expandCode = e => e.currentTarget.classList.toggle('expand-done') + + // 獲取隱藏狀態下元素的真實高度 + const getActualHeight = item => { + const hiddenElements = new Map() + + const fix = () => { + let current = item + while (current !== document.body && current != null) { + if (window.getComputedStyle(current).display === 'none') { + hiddenElements.set(current, current.getAttribute('style') || '') + } + current = current.parentNode + } + + const style = 'visibility: hidden !important; display: block !important;' + hiddenElements.forEach((originalStyle, elem) => { + elem.setAttribute('style', originalStyle ? originalStyle + ';' + style : style) + }) + } + + const restore = () => { + hiddenElements.forEach((originalStyle, elem) => { + if (originalStyle === '') elem.removeAttribute('style') + else elem.setAttribute('style', originalStyle) + }) + } + + fix() + const height = item.offsetHeight + restore() + return height + } + + const createEle = (lang, item) => { + const fragment = document.createDocumentFragment() + + if (isShowTool) { + const hlTools = document.createElement('div') + hlTools.className = `highlight-tools ${highlightShrinkClass}` + hlTools.innerHTML = highlightMacStyleEle + highlightShrinkEle + lang + highlightCopyEle + highlightFullpageEle + btf.addEventListenerPjax(hlTools, 'click', highlightToolsFn) + fragment.appendChild(hlTools) + } + + if (highlightHeightLimit && getActualHeight(item) > highlightHeightLimit + 30) { + const ele = document.createElement('div') + ele.className = 'code-expand-btn' + ele.innerHTML = '' + btf.addEventListenerPjax(ele, 'click', expandCode) + fragment.appendChild(ele) + } + + isPrismjs ? item.parentNode.insertBefore(fragment, item) : item.insertBefore(fragment, item.firstChild) + } + + $figureHighlight.forEach(item => { + let langName = '' + if (isPrismjs) btf.wrap(item, 'figure', { class: 'highlight' }) + + if (!highlightLang) { + createEle('', item) + return + } + + if (isPrismjs) { + langName = item.getAttribute('data-language') || 'Code' + } else { + langName = item.getAttribute('class').split(' ')[1] + if (langName === 'plain' || langName === undefined) langName = 'Code' + } + createEle(`
${langName}
`, item) + }) + } + + /** + * PhotoFigcaption + */ + const addPhotoFigcaption = () => { + if (!GLOBAL_CONFIG.isPhotoFigcaption) return + document.querySelectorAll('#article-container img').forEach(item => { + const altValue = item.title || item.alt + if (!altValue) return + const ele = document.createElement('div') + ele.className = 'img-alt text-center' + ele.textContent = altValue + item.insertAdjacentElement('afterend', ele) + }) + } + + /** + * Lightbox + */ + const runLightbox = () => { + btf.loadLightbox(document.querySelectorAll('#article-container img:not(.no-lightbox)')) + } + + /** + * justified-gallery 圖庫排版 + */ + + const fetchUrl = async url => { + const response = await fetch(url) + return await response.json() + } + + const runJustifiedGallery = (item, data, isButton = false, tabs) => { + const dataLength = data.length + + const ig = new InfiniteGrid.JustifiedInfiniteGrid(item, { + gap: 5, + isConstantSize: true, + sizeRange: [150, 600], + // useResizeObserver: true, + // observeChildren: true, + useTransform: true + // useRecycle: false + }) + + const replaceDq = str => str.replace(/"/g, '"') // replace double quotes to " + + const getItems = (nextGroupKey, count) => { + const nextItems = [] + const startCount = (nextGroupKey - 1) * count + + for (let i = 0; i < count; ++i) { + const num = startCount + i + if (num >= dataLength) { + break + } + + const item = data[num] + const alt = item.alt ? `alt="${replaceDq(item.alt)}"` : '' + const title = item.title ? `title="${replaceDq(item.title)}"` : '' + + nextItems.push(`
+ +
`) + } + return nextItems + } + + const buttonText = GLOBAL_CONFIG.infinitegrid.buttonText + const addButton = item => { + const button = document.createElement('button') + button.innerHTML = buttonText + '' + + button.addEventListener('click', e => { + e.target.closest('button').remove() + btf.setLoading.add(item) + appendItem(ig.getGroups().length + 1, 10) + }, { once: true }) + + item.insertAdjacentElement('afterend', button) + } + + const appendItem = (nextGroupKey, count) => { + ig.append(getItems(nextGroupKey, count), nextGroupKey) + } + + const maxGroupKey = Math.ceil(dataLength / 10) + let isLayoutHidden = false + + const completeFn = e => { + if (tabs) { + const parentNode = item.parentNode + + if (isLayoutHidden) { + parentNode.style.visibility = 'visible' + } + + if (item.offsetHeight === 0) { + parentNode.style.visibility = 'hidden' + isLayoutHidden = true + } + } + + const { updated, isResize, mounted } = e + if (!updated.length || !mounted.length || isResize) { + return + } + + btf.loadLightbox(item.querySelectorAll('img:not(.medium-zoom-image)')) + + if (ig.getGroups().length === maxGroupKey) { + btf.setLoading.remove(item) + !tabs && ig.off('renderComplete', completeFn) + return + } + + if (isButton) { + btf.setLoading.remove(item) + addButton(item) + } + } + + const requestAppendFn = btf.debounce(e => { + const nextGroupKey = (+e.groupKey || 0) + 1 + appendItem(nextGroupKey, 10) + + if (nextGroupKey === maxGroupKey) { + ig.off('requestAppend', requestAppendFn) + } + }, 300) + + btf.setLoading.add(item) + ig.on('renderComplete', completeFn) + + if (isButton) { + appendItem(1, 10) + } else { + ig.on('requestAppend', requestAppendFn) + ig.renderItems() + } + + btf.addGlobalFn('pjaxSendOnce', () => { ig.destroy() }) + } + + const addJustifiedGallery = async (ele, tabs = false) => { + if (!ele.length) return + const init = async () => { + for (const item of ele) { + if (btf.isHidden(item) || item.classList.contains('loaded')) continue + + const isButton = item.getAttribute('data-button') === 'true' + const children = item.firstElementChild + const text = children.textContent + children.textContent = '' + item.classList.add('loaded') + try { + const content = item.getAttribute('data-type') === 'url' ? await fetchUrl(text) : JSON.parse(text) + runJustifiedGallery(children, content, isButton, tabs) + } catch (e) { + console.error('Gallery data parsing failed:', e) + } + } + } + + if (typeof InfiniteGrid === 'function') { + init() + } else { + await btf.getScript(`${GLOBAL_CONFIG.infinitegrid.js}`) + init() + } + } + + /** + * rightside scroll percent + */ + const rightsideScrollPercent = currentTop => { + const scrollPercent = btf.getScrollPercent(currentTop, document.body) + const goUpElement = document.getElementById('go-up') + + if (scrollPercent < 95) { + goUpElement.classList.add('show-percent') + goUpElement.querySelector('.scroll-percent').textContent = scrollPercent + } else { + goUpElement.classList.remove('show-percent') + } + } + + /** + * 滾動處理 + */ + const scrollFn = () => { + const $rightside = document.getElementById('rightside') + const innerHeight = window.innerHeight + 56 + let initTop = 0 + const $header = document.getElementById('page-header') + const isChatBtn = typeof chatBtn !== 'undefined' + const isShowPercent = GLOBAL_CONFIG.percent.rightside + + // 檢查文檔高度是否小於視窗高度 + const checkDocumentHeight = () => { + if (document.body.scrollHeight <= innerHeight) { + $rightside.classList.add('rightside-show') + return true + } + return false + } + + // 如果文檔高度小於視窗高度,直接返回 + if (checkDocumentHeight()) return + + // find the scroll direction + const scrollDirection = currentTop => { + const result = currentTop > initTop // true is down & false is up + initTop = currentTop + return result + } + + let flag = '' + const scrollTask = btf.throttle(() => { + const currentTop = window.scrollY || document.documentElement.scrollTop + const isDown = scrollDirection(currentTop) + if (currentTop > 56) { + if (flag === '') { + $header.classList.add('nav-fixed') + $rightside.classList.add('rightside-show') + } + + if (isDown) { + if (flag !== 'down') { + $header.classList.remove('nav-visible') + isChatBtn && window.chatBtn.hide() + flag = 'down' + } + } else { + if (flag !== 'up') { + $header.classList.add('nav-visible') + isChatBtn && window.chatBtn.show() + flag = 'up' + } + } + } else { + flag = '' + if (currentTop === 0) { + $header.classList.remove('nav-fixed', 'nav-visible') + } + $rightside.classList.remove('rightside-show') + } + + isShowPercent && rightsideScrollPercent(currentTop) + checkDocumentHeight() + }, 300) + + btf.addEventListenerPjax(window, 'scroll', scrollTask, { passive: true }) + } + + /** + * toc,anchor + */ + const scrollFnToDo = () => { + const isToc = GLOBAL_CONFIG_SITE.isToc + const isAnchor = GLOBAL_CONFIG.isAnchor + const $article = document.getElementById('article-container') + + if (!($article && (isToc || isAnchor))) return + + let $tocLink, $cardToc, autoScrollToc, $tocPercentage, isExpand + + if (isToc) { + const $cardTocLayout = document.getElementById('card-toc') + $cardToc = $cardTocLayout.querySelector('.toc-content') + $tocLink = $cardToc.querySelectorAll('.toc-link') + $tocPercentage = $cardTocLayout.querySelector('.toc-percentage') + isExpand = $cardToc.classList.contains('is-expand') + + // toc元素點擊 + const tocItemClickFn = e => { + const target = e.target.closest('.toc-link') + if (!target) return + + e.preventDefault() + btf.scrollToDest(btf.getEleTop(document.getElementById(decodeURI(target.getAttribute('href')).replace('#', ''))), 300) + if (window.innerWidth < 900) { + $cardTocLayout.classList.remove('open') + } + } + + btf.addEventListenerPjax($cardToc, 'click', tocItemClickFn) + + autoScrollToc = item => { + const sidebarHeight = $cardToc.clientHeight + const itemOffsetTop = item.offsetTop + const itemHeight = item.clientHeight + const scrollTop = $cardToc.scrollTop + const offset = itemOffsetTop - scrollTop + const middlePosition = (sidebarHeight - itemHeight) / 2 + + if (offset !== middlePosition) { + $cardToc.scrollTop = scrollTop + (offset - middlePosition) + } + } + + // 處理 hexo-blog-encrypt 事件 + $cardToc.style.display = 'block' + } + + // find head position & add active class + const $articleList = $article.querySelectorAll('h1,h2,h3,h4,h5,h6') + let detectItem = '' + + const findHeadPosition = top => { + if (top === 0) return false + + let currentId = '' + let currentIndex = '' + + for (let i = 0; i < $articleList.length; i++) { + const ele = $articleList[i] + if (top > btf.getEleTop(ele) - 80) { + const id = ele.id + currentId = id ? '#' + encodeURI(id) : '' + currentIndex = i + } else { + break + } + } + + if (detectItem === currentIndex) return + + if (isAnchor) btf.updateAnchor(currentId) + + detectItem = currentIndex + + if (isToc) { + $cardToc.querySelectorAll('.active').forEach(i => i.classList.remove('active')) + + if (currentId) { + const currentActive = $tocLink[currentIndex] + currentActive.classList.add('active') + + setTimeout(() => autoScrollToc(currentActive), 0) + + if (!isExpand) { + let parent = currentActive.parentNode + while (!parent.matches('.toc')) { + if (parent.matches('li')) parent.classList.add('active') + parent = parent.parentNode + } + } + } + } + } + + // main of scroll + const tocScrollFn = btf.throttle(() => { + const currentTop = window.scrollY || document.documentElement.scrollTop + if (isToc && GLOBAL_CONFIG.percent.toc) { + $tocPercentage.textContent = btf.getScrollPercent(currentTop, $article) + } + findHeadPosition(currentTop) + }, 100) + + btf.addEventListenerPjax(window, 'scroll', tocScrollFn, { passive: true }) + } + + const handleThemeChange = mode => { + const globalFn = window.globalFn || {} + const themeChange = globalFn.themeChange || {} + if (!themeChange) { + return + } + + Object.keys(themeChange).forEach(key => { + const themeChangeFn = themeChange[key] + if (['disqus', 'disqusjs'].includes(key)) { + setTimeout(() => themeChangeFn(mode), 300) + } else { + themeChangeFn(mode) + } + }) + } + + /** + * Rightside + */ + const rightSideFn = { + readmode: () => { // read mode + const $body = document.body + const newEle = document.createElement('button') + + const exitReadMode = () => { + $body.classList.remove('read-mode') + newEle.remove() + newEle.removeEventListener('click', exitReadMode) + } + + $body.classList.add('read-mode') + newEle.type = 'button' + newEle.className = 'fas fa-sign-out-alt exit-readmode' + newEle.addEventListener('click', exitReadMode) + $body.appendChild(newEle) + }, + darkmode: () => { // switch between light and dark mode + const willChangeMode = document.documentElement.getAttribute('data-theme') === 'dark' ? 'light' : 'dark' + if (willChangeMode === 'dark') { + btf.activateDarkMode() + GLOBAL_CONFIG.Snackbar !== undefined && btf.snackbarShow(GLOBAL_CONFIG.Snackbar.day_to_night) + } else { + btf.activateLightMode() + GLOBAL_CONFIG.Snackbar !== undefined && btf.snackbarShow(GLOBAL_CONFIG.Snackbar.night_to_day) + } + btf.saveToLocal.set('theme', willChangeMode, 2) + handleThemeChange(willChangeMode) + }, + 'rightside-config': item => { // Show or hide rightside-hide-btn + const hideLayout = item.firstElementChild + if (hideLayout.classList.contains('show')) { + hideLayout.classList.add('status') + setTimeout(() => { + hideLayout.classList.remove('status') + }, 300) + } + + hideLayout.classList.toggle('show') + }, + 'go-up': () => { // Back to top + btf.scrollToDest(0, 500) + }, + 'hide-aside-btn': () => { // Hide aside + const $htmlDom = document.documentElement.classList + const saveStatus = $htmlDom.contains('hide-aside') ? 'show' : 'hide' + btf.saveToLocal.set('aside-status', saveStatus, 2) + $htmlDom.toggle('hide-aside') + }, + 'mobile-toc-button': (p, item) => { // Show mobile toc + const tocEle = document.getElementById('card-toc') + tocEle.style.transition = 'transform 0.3s ease-in-out' + + const tocEleHeight = tocEle.clientHeight + const btData = item.getBoundingClientRect() + + const tocEleBottom = window.innerHeight - btData.bottom - 30 + if (tocEleHeight > tocEleBottom) { + tocEle.style.transformOrigin = `right ${tocEleHeight - tocEleBottom - btData.height / 2}px` + } + + tocEle.classList.toggle('open') + tocEle.addEventListener('transitionend', () => { + tocEle.style.cssText = '' + }, { once: true }) + }, + 'chat-btn': () => { // Show chat + window.chatBtnFn() + }, + translateLink: () => { // switch between traditional and simplified chinese + window.translateFn.translatePage() + } + } + + document.getElementById('rightside').addEventListener('click', e => { + const $target = e.target.closest('[id]') + if ($target && rightSideFn[$target.id]) { + rightSideFn[$target.id](e.currentTarget, $target) + } + }) + + /** + * menu + * 側邊欄sub-menu 展開/收縮 + */ + const clickFnOfSubMenu = () => { + const handleClickOfSubMenu = e => { + const target = e.target.closest('.site-page.group') + if (!target) return + target.classList.toggle('hide') + } + + const menusItems = document.querySelector('#sidebar-menus .menus_items') + menusItems && menusItems.addEventListener('click', handleClickOfSubMenu) + } + + /** + * 手机端目录点击 + */ + const openMobileMenu = () => { + const toggleMenu = document.getElementById('toggle-menu') + if (!toggleMenu) return + btf.addEventListenerPjax(toggleMenu, 'click', () => { sidebarFn.open() }) + } + + /** + * 複製時加上版權信息 + */ + const addCopyright = () => { + const { limitCount, languages } = GLOBAL_CONFIG.copyright + + const handleCopy = (e) => { + e.preventDefault() + const copyFont = window.getSelection(0).toString() + let textFont = copyFont + if (copyFont.length > limitCount) { + textFont = `${copyFont}\n\n\n${languages.author}\n${languages.link}${window.location.href}\n${languages.source}\n${languages.info}` + } + if (e.clipboardData) { + return e.clipboardData.setData('text', textFont) + } else { + return window.clipboardData.setData('text', textFont) + } + } + + document.body.addEventListener('copy', handleCopy) + } + + /** + * 網頁運行時間 + */ + const addRuntime = () => { + const $runtimeCount = document.getElementById('runtimeshow') + if ($runtimeCount) { + const publishDate = $runtimeCount.getAttribute('data-publishDate') + $runtimeCount.textContent = `${btf.diffDate(publishDate)} ${GLOBAL_CONFIG.runtime}` + } + } + + /** + * 最後一次更新時間 + */ + const addLastPushDate = () => { + const $lastPushDateItem = document.getElementById('last-push-date') + if ($lastPushDateItem) { + const lastPushDate = $lastPushDateItem.getAttribute('data-lastPushDate') + $lastPushDateItem.textContent = btf.diffDate(lastPushDate, true) + } + } + + /** + * table overflow + */ + const addTableWrap = () => { + const $table = document.querySelectorAll('#article-container table') + if (!$table.length) return + + $table.forEach(item => { + if (!item.closest('.highlight')) { + btf.wrap(item, 'div', { class: 'table-wrap' }) + } + }) + } + + /** + * tag-hide + */ + const clickFnOfTagHide = () => { + const hideButtons = document.querySelectorAll('#article-container .hide-button') + if (!hideButtons.length) return + hideButtons.forEach(item => item.addEventListener('click', e => { + const currentTarget = e.currentTarget + currentTarget.classList.add('open') + addJustifiedGallery(currentTarget.nextElementSibling.querySelectorAll('.gallery-container')) + }, { once: true })) + } + + const tabsFn = () => { + const navTabsElements = document.querySelectorAll('#article-container .tabs') + if (!navTabsElements.length) return + + const setActiveClass = (elements, activeIndex) => { + elements.forEach((el, index) => { + el.classList.toggle('active', index === activeIndex) + }) + } + + const handleNavClick = e => { + const target = e.target.closest('button') + if (!target || target.classList.contains('active')) return + + const navItems = [...e.currentTarget.children] + const tabContents = [...e.currentTarget.nextElementSibling.children] + const indexOfButton = navItems.indexOf(target) + setActiveClass(navItems, indexOfButton) + e.currentTarget.classList.remove('no-default') + setActiveClass(tabContents, indexOfButton) + addJustifiedGallery(tabContents[indexOfButton].querySelectorAll('.gallery-container'), true) + } + + const handleToTopClick = tabElement => e => { + if (e.target.closest('button')) { + btf.scrollToDest(btf.getEleTop(tabElement), 300) + } + } + + navTabsElements.forEach(tabElement => { + btf.addEventListenerPjax(tabElement.firstElementChild, 'click', handleNavClick) + btf.addEventListenerPjax(tabElement.lastElementChild, 'click', handleToTopClick(tabElement)) + }) + } + + const toggleCardCategory = () => { + const cardCategory = document.querySelector('#aside-cat-list.expandBtn') + if (!cardCategory) return + + const handleToggleBtn = e => { + const target = e.target + if (target.nodeName === 'I') { + e.preventDefault() + target.parentNode.classList.toggle('expand') + } + } + btf.addEventListenerPjax(cardCategory, 'click', handleToggleBtn, true) + } + + const addPostOutdateNotice = () => { + const ele = document.getElementById('post-outdate-notice') + if (!ele) return + + const { limitDay, messagePrev, messageNext, postUpdate } = JSON.parse(ele.getAttribute('data')) + const diffDay = btf.diffDate(postUpdate) + if (diffDay >= limitDay) { + ele.textContent = `${messagePrev} ${diffDay} ${messageNext}` + ele.hidden = false + } + } + + const lazyloadImg = () => { + window.lazyLoadInstance = new LazyLoad({ + elements_selector: 'img', + threshold: 0, + data_src: 'lazy-src' + }) + + btf.addGlobalFn('pjaxComplete', () => { + window.lazyLoadInstance.update() + }, 'lazyload') + } + + const relativeDate = selector => { + selector.forEach(item => { + item.textContent = btf.diffDate(item.getAttribute('datetime'), true) + item.style.display = 'inline' + }) + } + + const justifiedIndexPostUI = () => { + const recentPostsElement = document.getElementById('recent-posts') + if (!(recentPostsElement && recentPostsElement.classList.contains('masonry'))) return + + const init = () => { + const masonryItem = new InfiniteGrid.MasonryInfiniteGrid('.recent-post-items', { + gap: { horizontal: 10, vertical: 20 }, + useTransform: true, + useResizeObserver: true + }) + masonryItem.renderItems() + btf.addGlobalFn('pjaxCompleteOnce', () => { masonryItem.destroy() }, 'removeJustifiedIndexPostUI') + } + + typeof InfiniteGrid === 'function' ? init() : btf.getScript(`${GLOBAL_CONFIG.infinitegrid.js}`).then(init) + } + + const unRefreshFn = () => { + window.addEventListener('resize', () => { + adjustMenu(false) + mobileSidebarOpen && btf.isHidden(document.getElementById('toggle-menu')) && sidebarFn.close() + }) + + const menuMask = document.getElementById('menu-mask') + menuMask && menuMask.addEventListener('click', () => { sidebarFn.close() }) + + clickFnOfSubMenu() + GLOBAL_CONFIG.islazyload && lazyloadImg() + GLOBAL_CONFIG.copyright !== undefined && addCopyright() + + if (GLOBAL_CONFIG.autoDarkmode) { + window.matchMedia('(prefers-color-scheme: dark)').addEventListener('change', e => { + if (btf.saveToLocal.get('theme') !== undefined) return + e.matches ? handleThemeChange('dark') : handleThemeChange('light') + }) + } + } + + const forPostFn = () => { + addHighlightTool() + addPhotoFigcaption() + addJustifiedGallery(document.querySelectorAll('#article-container .gallery-container')) + runLightbox() + scrollFnToDo() + addTableWrap() + clickFnOfTagHide() + tabsFn() + } + + const refreshFn = () => { + initAdjust() + justifiedIndexPostUI() + + if (GLOBAL_CONFIG_SITE.isPost) { + addPostOutdateNotice() + GLOBAL_CONFIG.relativeDate.post && relativeDate(document.querySelectorAll('#post-meta time')) + } else { + GLOBAL_CONFIG.relativeDate.homepage && relativeDate(document.querySelectorAll('#recent-posts time')) + GLOBAL_CONFIG.runtime && addRuntime() + addLastPushDate() + toggleCardCategory() + } + + GLOBAL_CONFIG_SITE.isHome && scrollDownInIndex() + scrollFn() + + forPostFn() + !GLOBAL_CONFIG_SITE.isShuoshuo && btf.switchComments(document) + openMobileMenu() + } + + btf.addGlobalFn('pjaxComplete', refreshFn, 'refreshFn') + refreshFn() + unRefreshFn() + + // 處理 hexo-blog-encrypt 事件 + window.addEventListener('hexo-blog-decrypt', e => { + forPostFn() + window.translateFn.translateInitialization() + Object.values(window.globalFn.encrypt).forEach(fn => { + fn() + }) + }) +}) diff --git a/js/search/algolia.js b/js/search/algolia.js new file mode 100644 index 0000000..8624f52 --- /dev/null +++ b/js/search/algolia.js @@ -0,0 +1,174 @@ +window.addEventListener('load', () => { + const { algolia } = GLOBAL_CONFIG + const { appId, apiKey, indexName, hitsPerPage = 5, languages } = algolia + + if (!appId || !apiKey || !indexName) { + return console.error('Algolia setting is invalid!') + } + + const $searchMask = document.getElementById('search-mask') + const $searchDialog = document.querySelector('#algolia-search .search-dialog') + + const animateElements = show => { + const action = show ? 'animateIn' : 'animateOut' + const maskAnimation = show ? 'to_show 0.5s' : 'to_hide 0.5s' + const dialogAnimation = show ? 'titleScale 0.5s' : 'search_close .5s' + btf[action]($searchMask, maskAnimation) + btf[action]($searchDialog, dialogAnimation) + } + + const fixSafariHeight = () => { + if (window.innerWidth < 768) { + $searchDialog.style.setProperty('--search-height', `${window.innerHeight}px`) + } + } + + const openSearch = () => { + btf.overflowPaddingR.add() + animateElements(true) + setTimeout(() => { document.querySelector('#algolia-search .ais-SearchBox-input').focus() }, 100) + + const handleEscape = event => { + if (event.code === 'Escape') { + closeSearch() + document.removeEventListener('keydown', handleEscape) + } + } + + document.addEventListener('keydown', handleEscape) + fixSafariHeight() + window.addEventListener('resize', fixSafariHeight) + } + + const closeSearch = () => { + btf.overflowPaddingR.remove() + animateElements(false) + window.removeEventListener('resize', fixSafariHeight) + } + + const searchClickFn = () => { + btf.addEventListenerPjax(document.querySelector('#search-button > .search'), 'click', openSearch) + } + + const searchFnOnce = () => { + $searchMask.addEventListener('click', closeSearch) + document.querySelector('#algolia-search .search-close-button').addEventListener('click', closeSearch) + } + + const cutContent = (content) => { + if (!content) return '' + const firstOccur = content.indexOf('') + let start = firstOccur - 30 + let end = firstOccur + 120 + let pre = '' + let post = '' + + if (start <= 0) { + start = 0 + end = 140 + } else { + pre = '...' + } + + if (end > content.length) { + end = content.length + } else { + post = '...' + } + + return `${pre}${content.substring(start, end)}${post}` + } + + const disableDiv = [ + document.getElementById('algolia-hits'), + document.getElementById('algolia-pagination'), + document.querySelector('#algolia-info .algolia-stats') + ] + + const searchClient = typeof algoliasearch === 'function' ? algoliasearch : window['algoliasearch/lite'].liteClient + const search = instantsearch({ + indexName, + searchClient: searchClient(appId, apiKey), + searchFunction (helper) { + disableDiv.forEach(item => { + item.style.display = helper.state.query ? '' : 'none' + }) + if (helper.state.query) helper.search() + } + }) + + const widgets = [ + instantsearch.widgets.configure({ hitsPerPage }), + instantsearch.widgets.searchBox({ + container: '#algolia-search-input', + showReset: false, + showSubmit: false, + placeholder: languages.input_placeholder, + showLoadingIndicator: true + }), + instantsearch.widgets.hits({ + container: '#algolia-hits', + templates: { + item (data) { + const link = data.permalink || (GLOBAL_CONFIG.root + data.path) + const result = data._highlightResult + const content = result.contentStripTruncate + ? cutContent(result.contentStripTruncate.value) + : result.contentStrip + ? cutContent(result.contentStrip.value) + : result.content + ? cutContent(result.content.value) + : '' + return ` + + ${result.title.value || 'no-title'} + ${content ? `
${content}
` : ''} + ` + }, + empty (data) { + return `
${languages.hits_empty.replace(/\$\{query}/, data.query)}
` + } + } + }), + instantsearch.widgets.stats({ + container: '#algolia-info > .algolia-stats', + templates: { + text (data) { + const stats = languages.hits_stats + .replace(/\$\{hits}/, data.nbHits) + .replace(/\$\{time}/, data.processingTimeMS) + return `
${stats}` + } + } + }), + instantsearch.widgets.poweredBy({ + container: '#algolia-info > .algolia-poweredBy' + }), + instantsearch.widgets.pagination({ + container: '#algolia-pagination', + totalPages: 5, + templates: { + first: '', + last: '', + previous: '', + next: '' + } + }) + ] + + search.addWidgets(widgets) + search.start() + searchClickFn() + searchFnOnce() + + window.addEventListener('pjax:complete', () => { + if (!btf.isHidden($searchMask)) closeSearch() + searchClickFn() + }) + + if (window.pjax) { + search.on('render', () => { + window.pjax.refresh(document.getElementById('algolia-hits')) + }) + } +}) diff --git a/js/search/local-search.js b/js/search/local-search.js new file mode 100644 index 0000000..1d3f268 --- /dev/null +++ b/js/search/local-search.js @@ -0,0 +1,360 @@ +/** + * Refer to hexo-generator-searchdb + * https://github.com/next-theme/hexo-generator-searchdb/blob/main/dist/search.js + * Modified by hexo-theme-butterfly + */ + +class LocalSearch { + constructor ({ + path = '', + unescape = false, + top_n_per_article = 1 + }) { + this.path = path + this.unescape = unescape + this.top_n_per_article = top_n_per_article + this.isfetched = false + this.datas = null + } + + getIndexByWord (words, text, caseSensitive = false) { + const index = [] + const included = new Set() + + if (!caseSensitive) { + text = text.toLowerCase() + } + words.forEach(word => { + if (this.unescape) { + const div = document.createElement('div') + div.innerText = word + word = div.innerHTML + } + const wordLen = word.length + if (wordLen === 0) return + let startPosition = 0 + let position = -1 + if (!caseSensitive) { + word = word.toLowerCase() + } + while ((position = text.indexOf(word, startPosition)) > -1) { + index.push({ position, word }) + included.add(word) + startPosition = position + wordLen + } + }) + // Sort index by position of keyword + index.sort((left, right) => { + if (left.position !== right.position) { + return left.position - right.position + } + return right.word.length - left.word.length + }) + return [index, included] + } + + // Merge hits into slices + mergeIntoSlice (start, end, index) { + let item = index[0] + let { position, word } = item + const hits = [] + const count = new Set() + while (position + word.length <= end && index.length !== 0) { + count.add(word) + hits.push({ + position, + length: word.length + }) + const wordEnd = position + word.length + + // Move to next position of hit + index.shift() + while (index.length !== 0) { + item = index[0] + position = item.position + word = item.word + if (wordEnd > position) { + index.shift() + } else { + break + } + } + } + return { + hits, + start, + end, + count: count.size + } + } + + // Highlight title and content + highlightKeyword (val, slice) { + let result = '' + let index = slice.start + for (const { position, length } of slice.hits) { + result += val.substring(index, position) + index = position + length + result += `${val.substr(position, length)}` + } + result += val.substring(index, slice.end) + return result + } + + getResultItems (keywords) { + const resultItems = [] + this.datas.forEach(({ title, content, url }) => { + // The number of different keywords included in the article. + const [indexOfTitle, keysOfTitle] = this.getIndexByWord(keywords, title) + const [indexOfContent, keysOfContent] = this.getIndexByWord(keywords, content) + const includedCount = new Set([...keysOfTitle, ...keysOfContent]).size + + // Show search results + const hitCount = indexOfTitle.length + indexOfContent.length + if (hitCount === 0) return + + const slicesOfTitle = [] + if (indexOfTitle.length !== 0) { + slicesOfTitle.push(this.mergeIntoSlice(0, title.length, indexOfTitle)) + } + + let slicesOfContent = [] + while (indexOfContent.length !== 0) { + const item = indexOfContent[0] + const { position } = item + // Cut out 120 characters. The maxlength of .search-input is 80. + const start = Math.max(0, position - 20) + const end = Math.min(content.length, position + 100) + slicesOfContent.push(this.mergeIntoSlice(start, end, indexOfContent)) + } + + // Sort slices in content by included keywords' count and hits' count + slicesOfContent.sort((left, right) => { + if (left.count !== right.count) { + return right.count - left.count + } else if (left.hits.length !== right.hits.length) { + return right.hits.length - left.hits.length + } + return left.start - right.start + }) + + // Select top N slices in content + const upperBound = parseInt(this.top_n_per_article, 10) + if (upperBound >= 0) { + slicesOfContent = slicesOfContent.slice(0, upperBound) + } + + let resultItem = '' + + url = new URL(url, location.origin) + url.searchParams.append('highlight', keywords.join(' ')) + + if (slicesOfTitle.length !== 0) { + resultItem += `
  • ${this.highlightKeyword(title, slicesOfTitle[0])}` + } else { + resultItem += `
  • ${title}` + } + + slicesOfContent.forEach(slice => { + resultItem += `

    ${this.highlightKeyword(content, slice)}...

    ` + }) + + resultItem += '
    • ' + resultItems.push({ + item: resultItem, + id: resultItems.length, + hitCount, + includedCount + }) + }) + return resultItems + } + + fetchData () { + const isXml = !this.path.endsWith('json') + fetch(this.path) + .then(response => response.text()) + .then(res => { + // Get the contents from search data + this.isfetched = true + this.datas = isXml + ? [...new DOMParser().parseFromString(res, 'text/xml').querySelectorAll('entry')].map(element => ({ + title: element.querySelector('title').textContent, + content: element.querySelector('content').textContent, + url: element.querySelector('url').textContent + })) + : JSON.parse(res) + // Only match articles with non-empty titles + this.datas = this.datas.filter(data => data.title).map(data => { + data.title = data.title.trim() + data.content = data.content ? data.content.trim().replace(/<[^>]+>/g, '') : '' + data.url = decodeURIComponent(data.url).replace(/\/{2,}/g, '/') + return data + }) + // Remove loading animation + window.dispatchEvent(new Event('search:loaded')) + }) + } + + // Highlight by wrapping node in mark elements with the given class name + highlightText (node, slice, className) { + const val = node.nodeValue + let index = slice.start + const children = [] + for (const { position, length } of slice.hits) { + const text = document.createTextNode(val.substring(index, position)) + index = position + length + const mark = document.createElement('mark') + mark.className = className + mark.appendChild(document.createTextNode(val.substr(position, length))) + children.push(text, mark) + } + node.nodeValue = val.substring(index, slice.end) + children.forEach(element => { + node.parentNode.insertBefore(element, node) + }) + } + + // Highlight the search words provided in the url in the text + highlightSearchWords (body) { + const params = new URL(location.href).searchParams.get('highlight') + const keywords = params ? params.split(' ') : [] + if (!keywords.length || !body) return + const walk = document.createTreeWalker(body, NodeFilter.SHOW_TEXT, null) + const allNodes = [] + while (walk.nextNode()) { + if (!walk.currentNode.parentNode.matches('button, select, textarea, .mermaid')) allNodes.push(walk.currentNode) + } + allNodes.forEach(node => { + const [indexOfNode] = this.getIndexByWord(keywords, node.nodeValue) + if (!indexOfNode.length) return + const slice = this.mergeIntoSlice(0, node.nodeValue.length, indexOfNode) + this.highlightText(node, slice, 'search-keyword') + }) + } +} + +window.addEventListener('load', () => { +// Search + const { path, top_n_per_article, unescape, languages } = GLOBAL_CONFIG.localSearch + const localSearch = new LocalSearch({ + path, + top_n_per_article, + unescape + }) + + const input = document.querySelector('#local-search-input input') + const statsItem = document.getElementById('local-search-stats-wrap') + const $loadingStatus = document.getElementById('loading-status') + const isXml = !path.endsWith('json') + + const inputEventFunction = () => { + if (!localSearch.isfetched) return + let searchText = input.value.trim().toLowerCase() + isXml && (searchText = searchText.replace(//g, '>')) + if (searchText !== '') $loadingStatus.innerHTML = '' + const keywords = searchText.split(/[-\s]+/) + const container = document.getElementById('local-search-results') + let resultItems = [] + if (searchText.length > 0) { + // Perform local searching + resultItems = localSearch.getResultItems(keywords) + } + if (keywords.length === 1 && keywords[0] === '') { + container.textContent = '' + statsItem.textContent = '' + } else if (resultItems.length === 0) { + container.textContent = '' + const statsDiv = document.createElement('div') + statsDiv.className = 'search-result-stats' + statsDiv.textContent = languages.hits_empty.replace(/\$\{query}/, searchText) + statsItem.innerHTML = statsDiv.outerHTML + } else { + resultItems.sort((left, right) => { + if (left.includedCount !== right.includedCount) { + return right.includedCount - left.includedCount + } else if (left.hitCount !== right.hitCount) { + return right.hitCount - left.hitCount + } + return right.id - left.id + }) + + const stats = languages.hits_stats.replace(/\$\{hits}/, resultItems.length) + + container.innerHTML = `
      ${resultItems.map(result => result.item).join('')}
    ` + statsItem.innerHTML = `
    ${stats}
    ` + window.pjax && window.pjax.refresh(container) + } + + $loadingStatus.textContent = '' + } + + let loadFlag = false + const $searchMask = document.getElementById('search-mask') + const $searchDialog = document.querySelector('#local-search .search-dialog') + + // fix safari + const fixSafariHeight = () => { + if (window.innerWidth < 768) { + $searchDialog.style.setProperty('--search-height', window.innerHeight + 'px') + } + } + + const openSearch = () => { + btf.overflowPaddingR.add() + btf.animateIn($searchMask, 'to_show 0.5s') + btf.animateIn($searchDialog, 'titleScale 0.5s') + setTimeout(() => { input.focus() }, 300) + if (!loadFlag) { + !localSearch.isfetched && localSearch.fetchData() + input.addEventListener('input', inputEventFunction) + loadFlag = true + } + // shortcut: ESC + document.addEventListener('keydown', function f (event) { + if (event.code === 'Escape') { + closeSearch() + document.removeEventListener('keydown', f) + } + }) + + fixSafariHeight() + window.addEventListener('resize', fixSafariHeight) + } + + const closeSearch = () => { + btf.overflowPaddingR.remove() + btf.animateOut($searchDialog, 'search_close .5s') + btf.animateOut($searchMask, 'to_hide 0.5s') + window.removeEventListener('resize', fixSafariHeight) + } + + const searchClickFn = () => { + btf.addEventListenerPjax(document.querySelector('#search-button > .search'), 'click', openSearch) + } + + const searchFnOnce = () => { + document.querySelector('#local-search .search-close-button').addEventListener('click', closeSearch) + $searchMask.addEventListener('click', closeSearch) + if (GLOBAL_CONFIG.localSearch.preload) { + localSearch.fetchData() + } + localSearch.highlightSearchWords(document.getElementById('article-container')) + } + + window.addEventListener('search:loaded', () => { + const $loadDataItem = document.getElementById('loading-database') + $loadDataItem.nextElementSibling.style.display = 'block' + $loadDataItem.remove() + }) + + searchClickFn() + searchFnOnce() + + // pjax + window.addEventListener('pjax:complete', () => { + !btf.isHidden($searchMask) && closeSearch() + localSearch.highlightSearchWords(document.getElementById('article-container')) + searchClickFn() + }) +}) diff --git a/js/tw_cn.js b/js/tw_cn.js new file mode 100644 index 0000000..c19d69c --- /dev/null +++ b/js/tw_cn.js @@ -0,0 +1,117 @@ +document.addEventListener('DOMContentLoaded', () => { + const { defaultEncoding, translateDelay, msgToTraditionalChinese, msgToSimplifiedChinese } = GLOBAL_CONFIG.translate + const snackbarData = GLOBAL_CONFIG.Snackbar + const targetEncodingCookie = 'translate-chn-cht' + + let currentEncoding = defaultEncoding + let targetEncoding = Number(btf.saveToLocal.get(targetEncodingCookie)) || defaultEncoding + const translateButtonObject = document.getElementById('translateLink') + const isSnackbar = snackbarData !== undefined + + const setLang = () => { + document.documentElement.lang = targetEncoding === 1 ? 'zh-TW' : 'zh-CN' + } + + const translateText = (txt) => { + if (!txt) return '' + if (currentEncoding === 1 && targetEncoding === 2) return Simplized(txt) + if (currentEncoding === 2 && targetEncoding === 1) return Traditionalized(txt) + return txt + } + + const translateBody = (fobj) => { + const nodes = typeof fobj === 'object' ? fobj.childNodes : document.body.childNodes + + for (const node of nodes) { + // Skip BR, HR tags, or the translate button object + if (['BR', 'HR'].includes(node.tagName) || node === translateButtonObject) continue + + if (node.nodeType === Node.ELEMENT_NODE) { + const { tagName, title, alt, placeholder, value, type } = node + + // Translate title, alt, placeholder + if (title) node.title = translateText(title) + if (alt) node.alt = translateText(alt) + if (placeholder) node.placeholder = translateText(placeholder) + + // Translate input value except text and hidden types + if (tagName === 'INPUT' && value && type !== 'text' && type !== 'hidden') { + node.value = translateText(value) + } + + // Recursively translate child nodes + translateBody(node) + } else if (node.nodeType === Node.TEXT_NODE) { + // Translate text node data + node.data = translateText(node.data) + } + } + } + + const translatePage = () => { + if (targetEncoding === 1) { + currentEncoding = 1 + targetEncoding = 2 + translateButtonObject.textContent = msgToTraditionalChinese + isSnackbar && btf.snackbarShow(snackbarData.cht_to_chs) + } else if (targetEncoding === 2) { + currentEncoding = 2 + targetEncoding = 1 + translateButtonObject.textContent = msgToSimplifiedChinese + isSnackbar && btf.snackbarShow(snackbarData.chs_to_cht) + } + btf.saveToLocal.set(targetEncodingCookie, targetEncoding, 2) + setLang() + translateBody() + } + + const JTPYStr = () => '万与丑专业丛东丝丢两严丧个丬丰临为丽举么义乌乐乔习乡书买乱争于亏云亘亚产亩亲亵亸亿仅从仑仓仪们价众优伙会伛伞伟传伤伥伦伧伪伫体余佣佥侠侣侥侦侧侨侩侪侬俣俦俨俩俪俭债倾偬偻偾偿傥傧储傩儿兑兖党兰关兴兹养兽冁内冈册写军农冢冯冲决况冻净凄凉凌减凑凛几凤凫凭凯击凼凿刍划刘则刚创删别刬刭刽刿剀剂剐剑剥剧劝办务劢动励劲劳势勋勐勚匀匦匮区医华协单卖卢卤卧卫却卺厂厅历厉压厌厍厕厢厣厦厨厩厮县参叆叇双发变叙叠叶号叹叽吁后吓吕吗吣吨听启吴呒呓呕呖呗员呙呛呜咏咔咙咛咝咤咴咸哌响哑哒哓哔哕哗哙哜哝哟唛唝唠唡唢唣唤唿啧啬啭啮啰啴啸喷喽喾嗫呵嗳嘘嘤嘱噜噼嚣嚯团园囱围囵国图圆圣圹场坂坏块坚坛坜坝坞坟坠垄垅垆垒垦垧垩垫垭垯垱垲垴埘埙埚埝埯堑堕塆墙壮声壳壶壸处备复够头夸夹夺奁奂奋奖奥妆妇妈妩妪妫姗姜娄娅娆娇娈娱娲娴婳婴婵婶媪嫒嫔嫱嬷孙学孪宁宝实宠审宪宫宽宾寝对寻导寿将尔尘尧尴尸尽层屃屉届属屡屦屿岁岂岖岗岘岙岚岛岭岳岽岿峃峄峡峣峤峥峦崂崃崄崭嵘嵚嵛嵝嵴巅巩巯币帅师帏帐帘帜带帧帮帱帻帼幂幞干并广庄庆庐庑库应庙庞废庼廪开异弃张弥弪弯弹强归当录彟彦彻径徕御忆忏忧忾怀态怂怃怄怅怆怜总怼怿恋恳恶恸恹恺恻恼恽悦悫悬悭悯惊惧惨惩惫惬惭惮惯愍愠愤愦愿慑慭憷懑懒懔戆戋戏戗战戬户扎扑扦执扩扪扫扬扰抚抛抟抠抡抢护报担拟拢拣拥拦拧拨择挂挚挛挜挝挞挟挠挡挢挣挤挥挦捞损捡换捣据捻掳掴掷掸掺掼揸揽揿搀搁搂搅携摄摅摆摇摈摊撄撑撵撷撸撺擞攒敌敛数斋斓斗斩断无旧时旷旸昙昼昽显晋晒晓晔晕晖暂暧札术朴机杀杂权条来杨杩杰极构枞枢枣枥枧枨枪枫枭柜柠柽栀栅标栈栉栊栋栌栎栏树栖样栾桊桠桡桢档桤桥桦桧桨桩梦梼梾检棂椁椟椠椤椭楼榄榇榈榉槚槛槟槠横樯樱橥橱橹橼檐檩欢欤欧歼殁殇残殒殓殚殡殴毁毂毕毙毡毵氇气氢氩氲汇汉污汤汹沓沟没沣沤沥沦沧沨沩沪沵泞泪泶泷泸泺泻泼泽泾洁洒洼浃浅浆浇浈浉浊测浍济浏浐浑浒浓浔浕涂涌涛涝涞涟涠涡涢涣涤润涧涨涩淀渊渌渍渎渐渑渔渖渗温游湾湿溃溅溆溇滗滚滞滟滠满滢滤滥滦滨滩滪漤潆潇潋潍潜潴澜濑濒灏灭灯灵灾灿炀炉炖炜炝点炼炽烁烂烃烛烟烦烧烨烩烫烬热焕焖焘煅煳熘爱爷牍牦牵牺犊犟状犷犸犹狈狍狝狞独狭狮狯狰狱狲猃猎猕猡猪猫猬献獭玑玙玚玛玮环现玱玺珉珏珐珑珰珲琎琏琐琼瑶瑷璇璎瓒瓮瓯电画畅畲畴疖疗疟疠疡疬疮疯疱疴痈痉痒痖痨痪痫痴瘅瘆瘗瘘瘪瘫瘾瘿癞癣癫癯皑皱皲盏盐监盖盗盘眍眦眬着睁睐睑瞒瞩矫矶矾矿砀码砖砗砚砜砺砻砾础硁硅硕硖硗硙硚确硷碍碛碜碱碹磙礼祎祢祯祷祸禀禄禅离秃秆种积称秽秾稆税稣稳穑穷窃窍窑窜窝窥窦窭竖竞笃笋笔笕笺笼笾筑筚筛筜筝筹签简箓箦箧箨箩箪箫篑篓篮篱簖籁籴类籼粜粝粤粪粮糁糇紧絷纟纠纡红纣纤纥约级纨纩纪纫纬纭纮纯纰纱纲纳纴纵纶纷纸纹纺纻纼纽纾线绀绁绂练组绅细织终绉绊绋绌绍绎经绐绑绒结绔绕绖绗绘给绚绛络绝绞统绠绡绢绣绤绥绦继绨绩绪绫绬续绮绯绰绱绲绳维绵绶绷绸绹绺绻综绽绾绿缀缁缂缃缄缅缆缇缈缉缊缋缌缍缎缏缐缑缒缓缔缕编缗缘缙缚缛缜缝缞缟缠缡缢缣缤缥缦缧缨缩缪缫缬缭缮缯缰缱缲缳缴缵罂网罗罚罢罴羁羟羡翘翙翚耢耧耸耻聂聋职聍联聩聪肃肠肤肷肾肿胀胁胆胜胧胨胪胫胶脉脍脏脐脑脓脔脚脱脶脸腊腌腘腭腻腼腽腾膑臜舆舣舰舱舻艰艳艹艺节芈芗芜芦苁苇苈苋苌苍苎苏苘苹茎茏茑茔茕茧荆荐荙荚荛荜荞荟荠荡荣荤荥荦荧荨荩荪荫荬荭荮药莅莜莱莲莳莴莶获莸莹莺莼萚萝萤营萦萧萨葱蒇蒉蒋蒌蓝蓟蓠蓣蓥蓦蔷蔹蔺蔼蕲蕴薮藁藓虏虑虚虫虬虮虽虾虿蚀蚁蚂蚕蚝蚬蛊蛎蛏蛮蛰蛱蛲蛳蛴蜕蜗蜡蝇蝈蝉蝎蝼蝾螀螨蟏衅衔补衬衮袄袅袆袜袭袯装裆裈裢裣裤裥褛褴襁襕见观觃规觅视觇览觉觊觋觌觍觎觏觐觑觞触觯詟誉誊讠计订讣认讥讦讧讨让讪讫训议讯记讱讲讳讴讵讶讷许讹论讻讼讽设访诀证诂诃评诅识诇诈诉诊诋诌词诎诏诐译诒诓诔试诖诗诘诙诚诛诜话诞诟诠诡询诣诤该详诧诨诩诪诫诬语诮误诰诱诲诳说诵诶请诸诹诺读诼诽课诿谀谁谂调谄谅谆谇谈谊谋谌谍谎谏谐谑谒谓谔谕谖谗谘谙谚谛谜谝谞谟谠谡谢谣谤谥谦谧谨谩谪谫谬谭谮谯谰谱谲谳谴谵谶谷豮贝贞负贠贡财责贤败账货质贩贪贫贬购贮贯贰贱贲贳贴贵贶贷贸费贺贻贼贽贾贿赀赁赂赃资赅赆赇赈赉赊赋赌赍赎赏赐赑赒赓赔赕赖赗赘赙赚赛赜赝赞赟赠赡赢赣赪赵赶趋趱趸跃跄跖跞践跶跷跸跹跻踊踌踪踬踯蹑蹒蹰蹿躏躜躯车轧轨轩轪轫转轭轮软轰轱轲轳轴轵轶轷轸轹轺轻轼载轾轿辀辁辂较辄辅辆辇辈辉辊辋辌辍辎辏辐辑辒输辔辕辖辗辘辙辚辞辩辫边辽达迁过迈运还这进远违连迟迩迳迹适选逊递逦逻遗遥邓邝邬邮邹邺邻郁郄郏郐郑郓郦郧郸酝酦酱酽酾酿释里鉅鉴銮錾钆钇针钉钊钋钌钍钎钏钐钑钒钓钔钕钖钗钘钙钚钛钝钞钟钠钡钢钣钤钥钦钧钨钩钪钫钬钭钮钯钰钱钲钳钴钵钶钷钸钹钺钻钼钽钾钿铀铁铂铃铄铅铆铈铉铊铋铍铎铏铐铑铒铕铗铘铙铚铛铜铝铞铟铠铡铢铣铤铥铦铧铨铪铫铬铭铮铯铰铱铲铳铴铵银铷铸铹铺铻铼铽链铿销锁锂锃锄锅锆锇锈锉锊锋锌锍锎锏锐锑锒锓锔锕锖锗错锚锜锞锟锠锡锢锣锤锥锦锨锩锫锬锭键锯锰锱锲锳锴锵锶锷锸锹锺锻锼锽锾锿镀镁镂镃镆镇镈镉镊镌镍镎镏镐镑镒镕镖镗镙镚镛镜镝镞镟镠镡镢镣镤镥镦镧镨镩镪镫镬镭镮镯镰镱镲镳镴镶长门闩闪闫闬闭问闯闰闱闲闳间闵闶闷闸闹闺闻闼闽闾闿阀阁阂阃阄阅阆阇阈阉阊阋阌阍阎阏阐阑阒阓阔阕阖阗阘阙阚阛队阳阴阵阶际陆陇陈陉陕陧陨险随隐隶隽难雏雠雳雾霁霉霭靓静靥鞑鞒鞯鞴韦韧韨韩韪韫韬韵页顶顷顸项顺须顼顽顾顿颀颁颂颃预颅领颇颈颉颊颋颌颍颎颏颐频颒颓颔颕颖颗题颙颚颛颜额颞颟颠颡颢颣颤颥颦颧风飏飐飑飒飓飔飕飖飗飘飙飚飞飨餍饤饥饦饧饨饩饪饫饬饭饮饯饰饱饲饳饴饵饶饷饸饹饺饻饼饽饾饿馀馁馂馃馄馅馆馇馈馉馊馋馌馍馎馏馐馑馒馓馔馕马驭驮驯驰驱驲驳驴驵驶驷驸驹驺驻驼驽驾驿骀骁骂骃骄骅骆骇骈骉骊骋验骍骎骏骐骑骒骓骔骕骖骗骘骙骚骛骜骝骞骟骠骡骢骣骤骥骦骧髅髋髌鬓魇魉鱼鱽鱾鱿鲀鲁鲂鲄鲅鲆鲇鲈鲉鲊鲋鲌鲍鲎鲏鲐鲑鲒鲓鲔鲕鲖鲗鲘鲙鲚鲛鲜鲝鲞鲟鲠鲡鲢鲣鲤鲥鲦鲧鲨鲩鲪鲫鲬鲭鲮鲯鲰鲱鲲鲳鲴鲵鲶鲷鲸鲹鲺鲻鲼鲽鲾鲿鳀鳁鳂鳃鳄鳅鳆鳇鳈鳉鳊鳋鳌鳍鳎鳏鳐鳑鳒鳓鳔鳕鳖鳗鳘鳙鳛鳜鳝鳞鳟鳠鳡鳢鳣鸟鸠鸡鸢鸣鸤鸥鸦鸧鸨鸩鸪鸫鸬鸭鸮鸯鸰鸱鸲鸳鸴鸵鸶鸷鸸鸹鸺鸻鸼鸽鸾鸿鹀鹁鹂鹃鹄鹅鹆鹇鹈鹉鹊鹋鹌鹍鹎鹏鹐鹑鹒鹓鹔鹕鹖鹗鹘鹚鹛鹜鹝鹞鹟鹠鹡鹢鹣鹤鹥鹦鹧鹨鹩鹪鹫鹬鹭鹯鹰鹱鹲鹳鹴鹾麦麸黄黉黡黩黪黾龙历志制一台皋准复猛钟注范签' + const FTPYStr = () => '萬與醜專業叢東絲丟兩嚴喪個爿豐臨為麗舉麼義烏樂喬習鄉書買亂爭於虧雲亙亞產畝親褻嚲億僅從侖倉儀們價眾優夥會傴傘偉傳傷倀倫傖偽佇體餘傭僉俠侶僥偵側僑儈儕儂俁儔儼倆儷儉債傾傯僂僨償儻儐儲儺兒兌兗黨蘭關興茲養獸囅內岡冊寫軍農塚馮衝決況凍淨淒涼淩減湊凜幾鳳鳧憑凱擊氹鑿芻劃劉則剛創刪別剗剄劊劌剴劑剮劍剝劇勸辦務勱動勵勁勞勢勳猛勩勻匭匱區醫華協單賣盧鹵臥衛卻巹廠廳曆厲壓厭厙廁廂厴廈廚廄廝縣參靉靆雙發變敘疊葉號歎嘰籲後嚇呂嗎唚噸聽啟吳嘸囈嘔嚦唄員咼嗆嗚詠哢嚨嚀噝吒噅鹹呱響啞噠嘵嗶噦嘩噲嚌噥喲嘜嗊嘮啢嗩唕喚呼嘖嗇囀齧囉嘽嘯噴嘍嚳囁嗬噯噓嚶囑嚕劈囂謔團園囪圍圇國圖圓聖壙場阪壞塊堅壇壢壩塢墳墜壟壟壚壘墾坰堊墊埡墶壋塏堖塒塤堝墊垵塹墮壪牆壯聲殼壺壼處備複夠頭誇夾奪奩奐奮獎奧妝婦媽嫵嫗媯姍薑婁婭嬈嬌孌娛媧嫻嫿嬰嬋嬸媼嬡嬪嬙嬤孫學孿寧寶實寵審憲宮寬賓寢對尋導壽將爾塵堯尷屍盡層屭屜屆屬屢屨嶼歲豈嶇崗峴嶴嵐島嶺嶽崠巋嶨嶧峽嶢嶠崢巒嶗崍嶮嶄嶸嶔崳嶁脊巔鞏巰幣帥師幃帳簾幟帶幀幫幬幘幗冪襆幹並廣莊慶廬廡庫應廟龐廢廎廩開異棄張彌弳彎彈強歸當錄彠彥徹徑徠禦憶懺憂愾懷態慫憮慪悵愴憐總懟懌戀懇惡慟懨愷惻惱惲悅愨懸慳憫驚懼慘懲憊愜慚憚慣湣慍憤憒願懾憖怵懣懶懍戇戔戲戧戰戩戶紮撲扡執擴捫掃揚擾撫拋摶摳掄搶護報擔擬攏揀擁攔擰撥擇掛摯攣掗撾撻挾撓擋撟掙擠揮撏撈損撿換搗據撚擄摑擲撣摻摜摣攬撳攙擱摟攪攜攝攄擺搖擯攤攖撐攆擷擼攛擻攢敵斂數齋斕鬥斬斷無舊時曠暘曇晝曨顯晉曬曉曄暈暉暫曖劄術樸機殺雜權條來楊榪傑極構樅樞棗櫪梘棖槍楓梟櫃檸檉梔柵標棧櫛櫳棟櫨櫟欄樹棲樣欒棬椏橈楨檔榿橋樺檜槳樁夢檮棶檢欞槨櫝槧欏橢樓欖櫬櫚櫸檟檻檳櫧橫檣櫻櫫櫥櫓櫞簷檁歡歟歐殲歿殤殘殞殮殫殯毆毀轂畢斃氈毿氌氣氫氬氳彙漢汙湯洶遝溝沒灃漚瀝淪滄渢溈滬濔濘淚澩瀧瀘濼瀉潑澤涇潔灑窪浹淺漿澆湞溮濁測澮濟瀏滻渾滸濃潯濜塗湧濤澇淶漣潿渦溳渙滌潤澗漲澀澱淵淥漬瀆漸澠漁瀋滲溫遊灣濕潰濺漵漊潷滾滯灩灄滿瀅濾濫灤濱灘澦濫瀠瀟瀲濰潛瀦瀾瀨瀕灝滅燈靈災燦煬爐燉煒熗點煉熾爍爛烴燭煙煩燒燁燴燙燼熱煥燜燾煆糊溜愛爺牘犛牽犧犢強狀獷獁猶狽麅獮獰獨狹獅獪猙獄猻獫獵獼玀豬貓蝟獻獺璣璵瑒瑪瑋環現瑲璽瑉玨琺瓏璫琿璡璉瑣瓊瑤璦璿瓔瓚甕甌電畫暢佘疇癤療瘧癘瘍鬁瘡瘋皰屙癰痙癢瘂癆瘓癇癡癉瘮瘞瘺癟癱癮癭癩癬癲臒皚皺皸盞鹽監蓋盜盤瞘眥矓著睜睞瞼瞞矚矯磯礬礦碭碼磚硨硯碸礪礱礫礎硜矽碩硤磽磑礄確鹼礙磧磣堿镟滾禮禕禰禎禱禍稟祿禪離禿稈種積稱穢穠穭稅穌穩穡窮竊竅窯竄窩窺竇窶豎競篤筍筆筧箋籠籩築篳篩簹箏籌簽簡籙簀篋籜籮簞簫簣簍籃籬籪籟糴類秈糶糲粵糞糧糝餱緊縶糸糾紆紅紂纖紇約級紈纊紀紉緯紜紘純紕紗綱納紝縱綸紛紙紋紡紵紖紐紓線紺絏紱練組紳細織終縐絆紼絀紹繹經紿綁絨結絝繞絰絎繪給絢絳絡絕絞統綆綃絹繡綌綏絛繼綈績緒綾緓續綺緋綽緔緄繩維綿綬繃綢綯綹綣綜綻綰綠綴緇緙緗緘緬纜緹緲緝縕繢緦綞緞緶線緱縋緩締縷編緡緣縉縛縟縝縫縗縞纏縭縊縑繽縹縵縲纓縮繆繅纈繚繕繒韁繾繰繯繳纘罌網羅罰罷羆羈羥羨翹翽翬耮耬聳恥聶聾職聹聯聵聰肅腸膚膁腎腫脹脅膽勝朧腖臚脛膠脈膾髒臍腦膿臠腳脫腡臉臘醃膕齶膩靦膃騰臏臢輿艤艦艙艫艱豔艸藝節羋薌蕪蘆蓯葦藶莧萇蒼苧蘇檾蘋莖蘢蔦塋煢繭荊薦薘莢蕘蓽蕎薈薺蕩榮葷滎犖熒蕁藎蓀蔭蕒葒葤藥蒞蓧萊蓮蒔萵薟獲蕕瑩鶯蓴蘀蘿螢營縈蕭薩蔥蕆蕢蔣蔞藍薊蘺蕷鎣驀薔蘞藺藹蘄蘊藪槁蘚虜慮虛蟲虯蟣雖蝦蠆蝕蟻螞蠶蠔蜆蠱蠣蟶蠻蟄蛺蟯螄蠐蛻蝸蠟蠅蟈蟬蠍螻蠑螿蟎蠨釁銜補襯袞襖嫋褘襪襲襏裝襠褌褳襝褲襇褸襤繈襴見觀覎規覓視覘覽覺覬覡覿覥覦覯覲覷觴觸觶讋譽謄訁計訂訃認譏訐訌討讓訕訖訓議訊記訒講諱謳詎訝訥許訛論訩訟諷設訪訣證詁訶評詛識詗詐訴診詆謅詞詘詔詖譯詒誆誄試詿詩詰詼誠誅詵話誕詬詮詭詢詣諍該詳詫諢詡譸誡誣語誚誤誥誘誨誑說誦誒請諸諏諾讀諑誹課諉諛誰諗調諂諒諄誶談誼謀諶諜謊諫諧謔謁謂諤諭諼讒諮諳諺諦謎諞諝謨讜謖謝謠謗諡謙謐謹謾謫譾謬譚譖譙讕譜譎讞譴譫讖穀豶貝貞負貟貢財責賢敗賬貨質販貪貧貶購貯貫貳賤賁貰貼貴貺貸貿費賀貽賊贄賈賄貲賃賂贓資賅贐賕賑賚賒賦賭齎贖賞賜贔賙賡賠賧賴賵贅賻賺賽賾贗讚贇贈贍贏贛赬趙趕趨趲躉躍蹌蹠躒踐躂蹺蹕躚躋踴躊蹤躓躑躡蹣躕躥躪躦軀車軋軌軒軑軔轉軛輪軟轟軲軻轤軸軹軼軤軫轢軺輕軾載輊轎輈輇輅較輒輔輛輦輩輝輥輞輬輟輜輳輻輯轀輸轡轅轄輾轆轍轔辭辯辮邊遼達遷過邁運還這進遠違連遲邇逕跡適選遜遞邐邏遺遙鄧鄺鄔郵鄒鄴鄰鬱郤郟鄶鄭鄆酈鄖鄲醞醱醬釅釃釀釋裏钜鑒鑾鏨釓釔針釘釗釙釕釷釺釧釤鈒釩釣鍆釹鍚釵鈃鈣鈈鈦鈍鈔鍾鈉鋇鋼鈑鈐鑰欽鈞鎢鉤鈧鈁鈥鈄鈕鈀鈺錢鉦鉗鈷缽鈳鉕鈽鈸鉞鑽鉬鉭鉀鈿鈾鐵鉑鈴鑠鉛鉚鈰鉉鉈鉍鈹鐸鉶銬銠鉺銪鋏鋣鐃銍鐺銅鋁銱銦鎧鍘銖銑鋌銩銛鏵銓鉿銚鉻銘錚銫鉸銥鏟銃鐋銨銀銣鑄鐒鋪鋙錸鋱鏈鏗銷鎖鋰鋥鋤鍋鋯鋨鏽銼鋝鋒鋅鋶鐦鐧銳銻鋃鋟鋦錒錆鍺錯錨錡錁錕錩錫錮鑼錘錐錦鍁錈錇錟錠鍵鋸錳錙鍥鍈鍇鏘鍶鍔鍤鍬鍾鍛鎪鍠鍰鎄鍍鎂鏤鎡鏌鎮鎛鎘鑷鐫鎳鎿鎦鎬鎊鎰鎔鏢鏜鏍鏰鏞鏡鏑鏃鏇鏐鐔钁鐐鏷鑥鐓鑭鐠鑹鏹鐙鑊鐳鐶鐲鐮鐿鑔鑣鑞鑲長門閂閃閆閈閉問闖閏闈閑閎間閔閌悶閘鬧閨聞闥閩閭闓閥閣閡閫鬮閱閬闍閾閹閶鬩閿閽閻閼闡闌闃闠闊闋闔闐闒闕闞闤隊陽陰陣階際陸隴陳陘陝隉隕險隨隱隸雋難雛讎靂霧霽黴靄靚靜靨韃鞽韉韝韋韌韍韓韙韞韜韻頁頂頃頇項順須頊頑顧頓頎頒頌頏預顱領頗頸頡頰頲頜潁熲頦頤頻頮頹頷頴穎顆題顒顎顓顏額顳顢顛顙顥纇顫顬顰顴風颺颭颮颯颶颸颼颻飀飄飆飆飛饗饜飣饑飥餳飩餼飪飫飭飯飲餞飾飽飼飿飴餌饒餉餄餎餃餏餅餑餖餓餘餒餕餜餛餡館餷饋餶餿饞饁饃餺餾饈饉饅饊饌饢馬馭馱馴馳驅馹駁驢駔駛駟駙駒騶駐駝駑駕驛駘驍罵駰驕驊駱駭駢驫驪騁驗騂駸駿騏騎騍騅騌驌驂騙騭騤騷騖驁騮騫騸驃騾驄驏驟驥驦驤髏髖髕鬢魘魎魚魛魢魷魨魯魴魺鮁鮃鯰鱸鮋鮓鮒鮊鮑鱟鮍鮐鮭鮚鮳鮪鮞鮦鰂鮜鱠鱭鮫鮮鮺鯗鱘鯁鱺鰱鰹鯉鰣鰷鯀鯊鯇鮶鯽鯒鯖鯪鯕鯫鯡鯤鯧鯝鯢鯰鯛鯨鯵鯴鯔鱝鰈鰏鱨鯷鰮鰃鰓鱷鰍鰒鰉鰁鱂鯿鰠鼇鰭鰨鰥鰩鰟鰜鰳鰾鱈鱉鰻鰵鱅鰼鱖鱔鱗鱒鱯鱤鱧鱣鳥鳩雞鳶鳴鳲鷗鴉鶬鴇鴆鴣鶇鸕鴨鴞鴦鴒鴟鴝鴛鴬鴕鷥鷙鴯鴰鵂鴴鵃鴿鸞鴻鵐鵓鸝鵑鵠鵝鵒鷳鵜鵡鵲鶓鵪鶤鵯鵬鵮鶉鶊鵷鷫鶘鶡鶚鶻鶿鶥鶩鷊鷂鶲鶹鶺鷁鶼鶴鷖鸚鷓鷚鷯鷦鷲鷸鷺鸇鷹鸌鸏鸛鸘鹺麥麩黃黌黶黷黲黽龍歷誌製壹臺臯準復勐鐘註範籤' + + const Traditionalized = (cc) => { + let str = '' + const ss = JTPYStr() + const tt = FTPYStr() + for (let i = 0; i < cc.length; i++) { + if (cc.charCodeAt(i) > 10000 && ss.indexOf(cc.charAt(i)) !== -1) { + str += tt.charAt(ss.indexOf(cc.charAt(i))) + } else str += cc.charAt(i) + } + return str + } + + const Simplized = (cc) => { + let str = '' + const ss = JTPYStr() + const tt = FTPYStr() + for (let i = 0; i < cc.length; i++) { + if (cc.charCodeAt(i) > 10000 && tt.indexOf(cc.charAt(i)) !== -1) { + str += ss.charAt(tt.indexOf(cc.charAt(i))) + } else str += cc.charAt(i) + } + return str + } + + const translateInitialization = () => { + if (translateButtonObject) { + if (currentEncoding !== targetEncoding) { + translateButtonObject.textContent = + targetEncoding === 1 + ? msgToSimplifiedChinese + : msgToTraditionalChinese + setLang() + setTimeout(translateBody, translateDelay) + } + } + } + + window.translateFn = { + translatePage, + Traditionalized, + Simplized, + translateInitialization + } + + translateInitialization() + btf.addGlobalFn('pjaxComplete', translateInitialization, 'translateInitialization') +}) diff --git a/js/utils.js b/js/utils.js new file mode 100644 index 0000000..48d8306 --- /dev/null +++ b/js/utils.js @@ -0,0 +1,313 @@ +(() => { + const btfFn = { + debounce: (func, wait = 0, immediate = false) => { + let timeout + return (...args) => { + const later = () => { + timeout = null + if (!immediate) func(...args) + } + const callNow = immediate && !timeout + clearTimeout(timeout) + timeout = setTimeout(later, wait) + if (callNow) func(...args) + } + }, + + throttle: function (func, wait, options = {}) { + let timeout, context, args + let previous = 0 + + const later = () => { + previous = options.leading === false ? 0 : new Date().getTime() + timeout = null + func.apply(context, args) + if (!timeout) context = args = null + } + + const throttled = (...params) => { + const now = new Date().getTime() + if (!previous && options.leading === false) previous = now + const remaining = wait - (now - previous) + context = this + args = params + if (remaining <= 0 || remaining > wait) { + if (timeout) { + clearTimeout(timeout) + timeout = null + } + previous = now + func.apply(context, args) + if (!timeout) context = args = null + } else if (!timeout && options.trailing !== false) { + timeout = setTimeout(later, remaining) + } + } + + return throttled + }, + + overflowPaddingR: { + add: () => { + const paddingRight = window.innerWidth - document.body.clientWidth + + if (paddingRight > 0) { + document.body.style.paddingRight = `${paddingRight}px` + document.body.style.overflow = 'hidden' + const menuElement = document.querySelector('#page-header.nav-fixed #menus') + if (menuElement) { + menuElement.style.paddingRight = `${paddingRight}px` + } + } + }, + remove: () => { + document.body.style.paddingRight = '' + document.body.style.overflow = '' + const menuElement = document.querySelector('#page-header.nav-fixed #menus') + if (menuElement) { + menuElement.style.paddingRight = '' + } + } + }, + + snackbarShow: (text, showAction = false, duration = 2000) => { + const { position, bgLight, bgDark } = GLOBAL_CONFIG.Snackbar + const bg = document.documentElement.getAttribute('data-theme') === 'light' ? bgLight : bgDark + Snackbar.show({ + text, + backgroundColor: bg, + showAction, + duration, + pos: position, + customClass: 'snackbar-css' + }) + }, + + diffDate: (inputDate, more = false) => { + const dateNow = new Date() + const datePost = new Date(inputDate) + const diffMs = dateNow - datePost + const diffSec = diffMs / 1000 + const diffMin = diffSec / 60 + const diffHour = diffMin / 60 + const diffDay = diffHour / 24 + const diffMonth = diffDay / 30 + const { dateSuffix } = GLOBAL_CONFIG + + if (!more) return Math.floor(diffDay) + + if (diffMonth > 12) return datePost.toISOString().slice(0, 10) + if (diffMonth >= 1) return `${Math.floor(diffMonth)} ${dateSuffix.month}` + if (diffDay >= 1) return `${Math.floor(diffDay)} ${dateSuffix.day}` + if (diffHour >= 1) return `${Math.floor(diffHour)} ${dateSuffix.hour}` + if (diffMin >= 1) return `${Math.floor(diffMin)} ${dateSuffix.min}` + return dateSuffix.just + }, + + loadComment: (dom, callback) => { + if ('IntersectionObserver' in window) { + const observerItem = new IntersectionObserver((entries) => { + if (entries[0].isIntersecting) { + callback() + observerItem.disconnect() + } + }, { threshold: [0] }) + observerItem.observe(dom) + } else { + callback() + } + }, + + scrollToDest: (pos, time = 500) => { + const currentPos = window.scrollY + const isNavFixed = document.getElementById('page-header').classList.contains('fixed') + if (currentPos > pos || isNavFixed) pos = pos - 70 + + if ('scrollBehavior' in document.documentElement.style) { + window.scrollTo({ + top: pos, + behavior: 'smooth' + }) + return + } + + const startTime = performance.now() + const animate = currentTime => { + const timeElapsed = currentTime - startTime + const progress = Math.min(timeElapsed / time, 1) + window.scrollTo(0, currentPos + (pos - currentPos) * progress) + if (progress < 1) { + requestAnimationFrame(animate) + } + } + requestAnimationFrame(animate) + }, + + animateIn: (ele, animation) => { + ele.style.display = 'block' + ele.style.animation = animation + }, + + animateOut: (ele, animation) => { + const handleAnimationEnd = () => { + ele.style.display = '' + ele.style.animation = '' + ele.removeEventListener('animationend', handleAnimationEnd) + } + ele.addEventListener('animationend', handleAnimationEnd) + ele.style.animation = animation + }, + + wrap: (selector, eleType, options) => { + const createEle = document.createElement(eleType) + for (const [key, value] of Object.entries(options)) { + createEle.setAttribute(key, value) + } + selector.parentNode.insertBefore(createEle, selector) + createEle.appendChild(selector) + }, + + isHidden: ele => ele.offsetHeight === 0 && ele.offsetWidth === 0, + + getEleTop: ele => { + let actualTop = ele.offsetTop + let current = ele.offsetParent + + while (current !== null) { + actualTop += current.offsetTop + current = current.offsetParent + } + + return actualTop + }, + + loadLightbox: ele => { + const service = GLOBAL_CONFIG.lightbox + + if (service === 'medium_zoom') { + mediumZoom(ele, { background: 'var(--zoom-bg)' }) + } + + if (service === 'fancybox') { + Array.from(ele).forEach(i => { + if (i.parentNode.tagName !== 'A') { + const dataSrc = i.dataset.lazySrc || i.src + const dataCaption = i.title || i.alt || '' + btf.wrap(i, 'a', { href: dataSrc, 'data-fancybox': 'gallery', 'data-caption': dataCaption, 'data-thumb': dataSrc }) + } + }) + + if (!window.fancyboxRun) { + Fancybox.bind('[data-fancybox]', { + Hash: false, + Thumbs: { + showOnStart: false + }, + Images: { + Panzoom: { + maxScale: 4 + } + }, + Carousel: { + transition: 'slide' + }, + Toolbar: { + display: { + left: ['infobar'], + middle: [ + 'zoomIn', + 'zoomOut', + 'toggle1to1', + 'rotateCCW', + 'rotateCW', + 'flipX', + 'flipY' + ], + right: ['slideshow', 'thumbs', 'close'] + } + } + }) + window.fancyboxRun = true + } + } + }, + + setLoading: { + add: ele => { + const html = ` +
    +
    +
    +
    +
    + ` + ele.insertAdjacentHTML('afterend', html) + }, + remove: ele => { + ele.nextElementSibling.remove() + } + }, + + updateAnchor: anchor => { + if (anchor !== window.location.hash) { + if (!anchor) anchor = location.pathname + const title = GLOBAL_CONFIG_SITE.title + window.history.replaceState({ + url: location.href, + title + }, title, anchor) + } + }, + + getScrollPercent: (() => { + let docHeight, winHeight, headerHeight, contentMath + + return (currentTop, ele) => { + if (!docHeight || ele.clientHeight !== docHeight) { + docHeight = ele.clientHeight + winHeight = window.innerHeight + headerHeight = ele.offsetTop + contentMath = Math.max(docHeight - winHeight, document.documentElement.scrollHeight - winHeight) + } + + const scrollPercent = (currentTop - headerHeight) / contentMath + return Math.max(0, Math.min(100, Math.round(scrollPercent * 100))) + } + })(), + + addEventListenerPjax: (ele, event, fn, option = false) => { + ele.addEventListener(event, fn, option) + btf.addGlobalFn('pjaxSendOnce', () => { + ele.removeEventListener(event, fn, option) + }) + }, + + removeGlobalFnEvent: (key, parent = window) => { + const globalFn = parent.globalFn || {} + const keyObj = globalFn[key] + if (!keyObj) return + + Object.keys(keyObj).forEach(i => keyObj[i]()) + + delete globalFn[key] + }, + + switchComments: (el = document, path) => { + const switchBtn = el.querySelector('#switch-btn') + if (!switchBtn) return + + let switchDone = false + const postComment = el.querySelector('#post-comment') + const handleSwitchBtn = () => { + postComment.classList.toggle('move') + if (!switchDone && typeof loadOtherComment === 'function') { + switchDone = true + loadOtherComment(el, path) + } + } + btf.addEventListenerPjax(switchBtn, 'click', handleSwitchBtn) + } + } + + window.btf = { ...window.btf, ...btfFn } +})() diff --git a/lib/hbe.js b/lib/hbe.js new file mode 100644 index 0000000..71205dd --- /dev/null +++ b/lib/hbe.js @@ -0,0 +1,297 @@ +(() => { + 'use strict'; + + const cryptoObj = window.crypto || window.msCrypto; + const storage = window.localStorage; + + const storageName = 'hexo-blog-encrypt:#' + window.location.pathname; + const keySalt = textToArray('hexo-blog-encrypt的作者们都是大帅比!'); + const ivSalt = textToArray('hexo-blog-encrypt是地表最强Hexo加密插件!'); + +// As we can't detect the wrong password with AES-CBC, +// so adding an empty div and check it when decrption. +const knownPrefix = ""; + + const mainElement = document.getElementById('hexo-blog-encrypt'); + const wrongPassMessage = mainElement.dataset['wpm']; + const wrongHashMessage = mainElement.dataset['whm']; + const dataElement = mainElement.getElementsByTagName('script')['hbeData']; + const encryptedData = dataElement.innerText; + const HmacDigist = dataElement.dataset['hmacdigest']; + + function hexToArray(s) { + return new Uint8Array(s.match(/[\da-f]{2}/gi).map((h => { + return parseInt(h, 16); + }))); + } + + function textToArray(s) { + var i = s.length; + var n = 0; + var ba = new Array() + + for (var j = 0; j < i;) { + var c = s.codePointAt(j); + if (c < 128) { + ba[n++] = c; + j++; + } else if ((c > 127) && (c < 2048)) { + ba[n++] = (c >> 6) | 192; + ba[n++] = (c & 63) | 128; + j++; + } else if ((c > 2047) && (c < 65536)) { + ba[n++] = (c >> 12) | 224; + ba[n++] = ((c >> 6) & 63) | 128; + ba[n++] = (c & 63) | 128; + j++; + } else { + ba[n++] = (c >> 18) | 240; + ba[n++] = ((c >> 12) & 63) | 128; + ba[n++] = ((c >> 6) & 63) | 128; + ba[n++] = (c & 63) | 128; + j += 2; + } + } + return new Uint8Array(ba); + } + + function arrayBufferToHex(arrayBuffer) { + if (typeof arrayBuffer !== 'object' || arrayBuffer === null || typeof arrayBuffer.byteLength !== 'number') { + throw new TypeError('Expected input to be an ArrayBuffer') + } + + var view = new Uint8Array(arrayBuffer) + var result = '' + var value + + for (var i = 0; i < view.length; i++) { + value = view[i].toString(16) + result += (value.length === 1 ? '0' + value : value) + } + + return result + } + + async function getExecutableScript(oldElem) { + let out = document.createElement('script'); + const attList = ['type', 'text', 'src', 'crossorigin', 'defer', 'referrerpolicy']; + attList.forEach((att) => { + if (oldElem[att]) + out[att] = oldElem[att]; + }) + + return out; + } + + async function convertHTMLToElement(content) { + let out = document.createElement('div'); + out.innerHTML = content; + out.querySelectorAll('script').forEach(async (elem) => { + elem.replaceWith(await getExecutableScript(elem)); + }); + + return out; + } + + function getKeyMaterial(password) { + let encoder = new TextEncoder(); + return cryptoObj.subtle.importKey( + 'raw', + encoder.encode(password), + { + 'name': 'PBKDF2', + }, + false, + [ + 'deriveKey', + 'deriveBits', + ] + ); + } + + function getHmacKey(keyMaterial) { + return cryptoObj.subtle.deriveKey({ + 'name': 'PBKDF2', + 'hash': 'SHA-256', + 'salt': keySalt.buffer, + 'iterations': 1024 + }, keyMaterial, { + 'name': 'HMAC', + 'hash': 'SHA-256', + 'length': 256, + }, true, [ + 'verify', + ]); + } + + function getDecryptKey(keyMaterial) { + return cryptoObj.subtle.deriveKey({ + 'name': 'PBKDF2', + 'hash': 'SHA-256', + 'salt': keySalt.buffer, + 'iterations': 1024, + }, keyMaterial, { + 'name': 'AES-CBC', + 'length': 256, + }, true, [ + 'decrypt', + ]); + } + + function getIv(keyMaterial) { + return cryptoObj.subtle.deriveBits({ + 'name': 'PBKDF2', + 'hash': 'SHA-256', + 'salt': ivSalt.buffer, + 'iterations': 512, + }, keyMaterial, 16 * 8); + } + + async function verifyContent(key, content) { + const encoder = new TextEncoder(); + const encoded = encoder.encode(content); + + let signature = hexToArray(HmacDigist); + + const result = await cryptoObj.subtle.verify({ + 'name': 'HMAC', + 'hash': 'SHA-256', + }, key, signature, encoded); + console.log(`Verification result: ${result}`); + if (!result) { + alert(wrongHashMessage); + console.log(`${wrongHashMessage}, got `, signature, ` but proved wrong.`); + } + return result; + } + + async function decrypt(decryptKey, iv, hmacKey) { + let typedArray = hexToArray(encryptedData); + + const result = await cryptoObj.subtle.decrypt({ + 'name': 'AES-CBC', + 'iv': iv, + }, decryptKey, typedArray.buffer).then(async (result) => { + const decoder = new TextDecoder(); + const decoded = decoder.decode(result); + + // check the prefix, if not then we can sure here is wrong password. + if (!decoded.startsWith(knownPrefix)) { + throw "Decode successfully but not start with KnownPrefix."; + } + + const hideButton = document.createElement('button'); + hideButton.textContent = 'Encrypt again'; + hideButton.type = 'button'; + hideButton.classList.add("hbe-button"); + hideButton.addEventListener('click', () => { + window.localStorage.removeItem(storageName); + window.location.reload(); + }); + + document.getElementById('hexo-blog-encrypt').style.display = 'inline'; + document.getElementById('hexo-blog-encrypt').innerHTML = ''; + document.getElementById('hexo-blog-encrypt').appendChild(await convertHTMLToElement(decoded)); + document.getElementById('hexo-blog-encrypt').appendChild(hideButton); + + // support html5 lazyload functionality. + document.querySelectorAll('img').forEach((elem) => { + if (elem.getAttribute("data-src") && !elem.src) { + elem.src = elem.getAttribute('data-src'); + } + }); + + // support theme-next refresh + window.NexT && NexT.boot && typeof NexT.boot.refresh === 'function' && NexT.boot.refresh(); + + // TOC part + var tocDiv = document.getElementById("toc-div"); + if (tocDiv) { + tocDiv.style.display = 'inline'; + } + + var tocDivs = document.getElementsByClassName('toc-div-class'); + if (tocDivs && tocDivs.length > 0) { + for (var idx = 0; idx < tocDivs.length; idx++) { + tocDivs[idx].style.display = 'inline'; + } + } + + // trigger event + var event = new Event('hexo-blog-decrypt'); + window.dispatchEvent(event); + + return await verifyContent(hmacKey, decoded); + }).catch((e) => { + alert(wrongPassMessage); + console.log(e); + return false; + }); + + return result; + + } + + function hbeLoader() { + + const oldStorageData = JSON.parse(storage.getItem(storageName)); + + if (oldStorageData) { + console.log(`Password got from localStorage(${storageName}): `, oldStorageData); + + const sIv = hexToArray(oldStorageData.iv).buffer; + const sDk = oldStorageData.dk; + const sHmk = oldStorageData.hmk; + + cryptoObj.subtle.importKey('jwk', sDk, { + 'name': 'AES-CBC', + 'length': 256, + }, true, [ + 'decrypt', + ]).then((dkCK) => { + cryptoObj.subtle.importKey('jwk', sHmk, { + 'name': 'HMAC', + 'hash': 'SHA-256', + 'length': 256, + }, true, [ + 'verify', + ]).then((hmkCK) => { + decrypt(dkCK, sIv, hmkCK).then((result) => { + if (!result) { + storage.removeItem(storageName); + } + }); + }); + }); + } + + mainElement.addEventListener('keydown', async (event) => { + if (event.isComposing || event.keyCode === 13) { + const password = document.getElementById('hbePass').value; + const keyMaterial = await getKeyMaterial(password); + const hmacKey = await getHmacKey(keyMaterial); + const decryptKey = await getDecryptKey(keyMaterial); + const iv = await getIv(keyMaterial); + + decrypt(decryptKey, iv, hmacKey).then((result) => { + console.log(`Decrypt result: ${result}`); + if (result) { + cryptoObj.subtle.exportKey('jwk', decryptKey).then((dk) => { + cryptoObj.subtle.exportKey('jwk', hmacKey).then((hmk) => { + const newStorageData = { + 'dk': dk, + 'iv': arrayBufferToHex(iv), + 'hmk': hmk, + }; + storage.setItem(storageName, JSON.stringify(newStorageData)); + }); + }); + } + }); + } + }); + } + + hbeLoader(); + +})(); diff --git a/link/index.html b/link/index.html new file mode 100644 index 0000000..53218de --- /dev/null +++ b/link/index.html @@ -0,0 +1,270 @@ +友链 | 正在施工中 + + + + + + + + + +

    友链

    友链

    +
    闲着没事干也做了博客的无聊人们
    +
    + +
    + Yangty +
    +
    Yangty
    +
    大神
    +     +
    +
    + +
    + swl +
    +
    swl
    +
    大神
    +     +
    +
    + +
    + Murasaki +
    +
    Murasaki
    +
    学数学学的
    +     +
    +
    + +
    + rosist-sallina +
    +
    rosist-sallina
    +
    于是批准马匹一周跑两天
    +     +
    +
    + +
    + ajssad +
    +
    ajssad
    +
    望着那象征命运的红绿灯
    +     +
    avatar
    zirno81
    Articles
    12
    Tags
    0
    Categories
    0
    Follow Me
    Announcement
    This is my Blog
    Recent Posts
    电子电路与系统基础（2）：（四）正反馈和负阻
    数理方程（4）：位势方程和Green函数法
    数理方程（五）分离变量法
    电子电路与系统基础（2）：（三）负反馈网络
    数理方程（3）：热传导方程和积分变换初步
    +
    + + Archives + +
    +
    Website Info
    Article Count :
    12
    Last Update :
    \ No newline at end of file diff --git a/page/2/index.html b/page/2/index.html new file mode 100644 index 0000000..2e6c13f --- /dev/null +++ b/page/2/index.html @@ -0,0 +1,238 @@ +正在施工中 - 而那未曾谋面的故事还在继续 + + + + + + + +

    正在施工中

    清华电子系数算 OJ 通关指北
    Created
    写在基石前面 下面这段话来自于 NJU 计算机系统概论 PA 文档，值得一读。 基础设施 - 提高项目开发的效率 在PA中, 基础设施是指支撑项目开发的各种工具和手段. 原则上基础设施并不属于课本知识的范畴, 但是作为一个有一定规模的项目, 基础设施的好坏会影响到项目的推进, 甚至决定项目的成败, 这是你在程序设计课上体会不到的. 事实上, 你已经体会过基础设施给你带来的便利了. 我们的框架代码已经提供了Makefile来对NEMU进行一键编译. 假设我们并没有提供一键编译的功能, 你需要通过手动键入gcc命令的方式来编译源文件: 假设你手动输入一条gcc命令需要10秒的时间(你还需要输入很多编译选项, 能用10秒输入完已经是非常快的了), 而NEMU工程下有30个源文件, 为了编译出NEMU的可执行文件, 你需要花费多少时间? 然而你还需要在开发NEMU的过程中不断进行编译, 假设你需要编译500次NEMU才能完成PA, 一学期下来, 你仅仅花在键入编译命令上的时间有多少? 有的项目即使使用工具也需要花费较多时间来构建....
    THUCTF 2023 部分 Writeup
    Created
    THUCTF 2023 Writeup Zirno_81 也许有 copyright 一道难题 base64 一眼顶针，下一个 easymaze 用 16 进制读取发现 IEND 数据块后面还有数据，Google 文件尾得知是倒着的 zip 头，于是乎提取出来做倒置得到压缩包（但是得到的压缩包有点损坏直接 WINRAR 修复了）。解压得到一个 linux 可执行文件，先拖进 16 进制读取器里面，得到了 flag1 的明文。 然后才学会用 IDA 逆向，于是乎 shift+F12 找到了奇怪的字符串，结合反编译伪代码猜测是一个迷宫，手动换行得到迷宫图 flag2 is THUCTF{wwdwwdddsssssd} 麦恩·库拉夫特 - 1 实际上可以 /gamemode spectator 然后发现正确路径直接冲就完事了 关注 THUCTF 谢谢喵 关注紫荆园食堂红色圆圈炒宫爆八十一谢谢喵 KFC 旁边那家店卖 taco，结合一下店名搜到疑似全世界唯一的这家店，于是直接结束 怎么这都要给图啊 简单的基本功 出题组是不是第一次给的压缩包有问题，我第一次获得的是一个 1kb...
    avatar
    zirno81
    Articles
    12
    Tags
    0
    Categories
    0
    Follow Me
    Announcement
    This is my Blog
    Recent Posts
    电子电路与系统基础（2）：（四）正反馈和负阻
    数理方程（4）：位势方程和Green函数法
    数理方程（五）分离变量法
    电子电路与系统基础（2）：（三）负反馈网络
    数理方程（3）：热传导方程和积分变换初步
    +
    + + Archives + +
    +
    Website Info
    Article Count :
    12
    Last Update :
    \ No newline at end of file diff --git a/pics/EEEC1/image-1.png b/pics/EEEC1/image-1.png new file mode 100644 index 0000000..00916f2 Binary files /dev/null and b/pics/EEEC1/image-1.png differ diff --git a/pics/EEEC1/image-2.png b/pics/EEEC1/image-2.png new file mode 100644 index 0000000..9062f2d Binary files /dev/null and b/pics/EEEC1/image-2.png differ diff --git a/pics/EEEC1/image-3.png b/pics/EEEC1/image-3.png new file mode 100644 index 0000000..98cac0e Binary files /dev/null and b/pics/EEEC1/image-3.png differ diff --git a/pics/EEEC1/image-4.png b/pics/EEEC1/image-4.png new file mode 100644 index 0000000..c1e361a Binary files /dev/null and b/pics/EEEC1/image-4.png differ diff --git a/pics/EEEC1/image.png b/pics/EEEC1/image.png new file mode 100644 index 0000000..667649b Binary files /dev/null and b/pics/EEEC1/image.png differ diff --git a/pics/EEEC2-2/image-20241123112317947.png b/pics/EEEC2-2/image-20241123112317947.png new file mode 100644 index 0000000..a44f363 Binary files /dev/null and b/pics/EEEC2-2/image-20241123112317947.png differ diff --git a/pics/EEEC2-2/image-20241123113105966.png b/pics/EEEC2-2/image-20241123113105966.png new file mode 100644 index 0000000..7d0a604 Binary files /dev/null and b/pics/EEEC2-2/image-20241123113105966.png differ diff --git a/pics/EEEC2-2/image-20241123131459676.png b/pics/EEEC2-2/image-20241123131459676.png new file mode 100644 index 0000000..ac92f5a Binary files /dev/null and b/pics/EEEC2-2/image-20241123131459676.png differ diff --git a/pics/EEEC2-2/image-20241123131712618.png b/pics/EEEC2-2/image-20241123131712618.png new file mode 100644 index 0000000..0fcbb8c Binary files /dev/null and b/pics/EEEC2-2/image-20241123131712618.png differ diff --git a/pics/EEEC2-2/image-20241123132201744.png b/pics/EEEC2-2/image-20241123132201744.png new file mode 100644 index 0000000..c770204 Binary files /dev/null and b/pics/EEEC2-2/image-20241123132201744.png differ diff --git a/pics/EEEC2-2/image-20241123132329135.png b/pics/EEEC2-2/image-20241123132329135.png new file mode 100644 index 0000000..3236c24 Binary files /dev/null and b/pics/EEEC2-2/image-20241123132329135.png differ diff --git a/pics/EEEC2-2/image-20241123133340548.png b/pics/EEEC2-2/image-20241123133340548.png new file mode 100644 index 0000000..20f2a16 Binary files /dev/null and b/pics/EEEC2-2/image-20241123133340548.png differ diff --git a/pics/EEEC2-2/image-20241123135932987.png b/pics/EEEC2-2/image-20241123135932987.png new file mode 100644 index 0000000..67b8040 Binary files /dev/null and b/pics/EEEC2-2/image-20241123135932987.png differ diff --git a/pics/EEEC2-2/image-20241123141947596.png b/pics/EEEC2-2/image-20241123141947596.png new file mode 100644 index 0000000..7bf2ac4 Binary files /dev/null and b/pics/EEEC2-2/image-20241123141947596.png differ diff --git a/pics/EEEC2-2/image-20241123150937701.png b/pics/EEEC2-2/image-20241123150937701.png new file mode 100644 index 0000000..ada40dc Binary files /dev/null and b/pics/EEEC2-2/image-20241123150937701.png differ diff --git a/pics/EEEC2-2/image-20241123152402925.png b/pics/EEEC2-2/image-20241123152402925.png new file mode 100644 index 0000000..86cc98f Binary files /dev/null and b/pics/EEEC2-2/image-20241123152402925.png differ diff --git a/pics/EEEC2-2/image-20241123155257856.png b/pics/EEEC2-2/image-20241123155257856.png new file mode 100644 index 0000000..f24e5d6 Binary files /dev/null and b/pics/EEEC2-2/image-20241123155257856.png differ diff --git a/pics/EEEC2-2/image-20241123160814100.png b/pics/EEEC2-2/image-20241123160814100.png new file mode 100644 index 0000000..39a1e35 Binary files /dev/null and b/pics/EEEC2-2/image-20241123160814100.png differ diff --git a/pics/EEEC2-2/image-20241123162808250.png b/pics/EEEC2-2/image-20241123162808250.png new file mode 100644 index 0000000..4d47147 Binary files /dev/null and b/pics/EEEC2-2/image-20241123162808250.png differ diff --git a/pics/EEEC2-2/image-20241123164451810.png b/pics/EEEC2-2/image-20241123164451810.png new file mode 100644 index 0000000..8fa7536 Binary files /dev/null and b/pics/EEEC2-2/image-20241123164451810.png differ diff --git a/pics/EEEC2-2/image-20241123165000343.png b/pics/EEEC2-2/image-20241123165000343.png new file mode 100644 index 0000000..2656479 Binary files /dev/null and b/pics/EEEC2-2/image-20241123165000343.png differ diff --git a/pics/EEEC2-2/image-20241123165034431.png b/pics/EEEC2-2/image-20241123165034431.png new file mode 100644 index 0000000..b5a8480 Binary files /dev/null and b/pics/EEEC2-2/image-20241123165034431.png differ diff --git a/pics/EEEC2-2/image-20241123165707052.png b/pics/EEEC2-2/image-20241123165707052.png new file mode 100644 index 0000000..82c31b4 Binary files /dev/null and b/pics/EEEC2-2/image-20241123165707052.png differ diff --git a/pics/EEEC2-2/image-20241123170048704.png b/pics/EEEC2-2/image-20241123170048704.png new file mode 100644 index 0000000..8a706b7 Binary files /dev/null and b/pics/EEEC2-2/image-20241123170048704.png differ diff --git "a/pics/EEEC2-2/\350\256\276\350\256\2411.ms14" "b/pics/EEEC2-2/\350\256\276\350\256\2411.ms14" new file mode 100644 index 0000000..d201882 Binary files /dev/null and "b/pics/EEEC2-2/\350\256\276\350\256\2411.ms14" differ diff --git "a/pics/EEEC2-2/\350\256\276\350\256\2412.ms14" "b/pics/EEEC2-2/\350\256\276\350\256\2412.ms14" new file mode 100644 index 0000000..39915c2 Binary files /dev/null and "b/pics/EEEC2-2/\350\256\276\350\256\2412.ms14" differ diff --git "a/pics/EEEC2-2/\350\256\276\350\256\2413.ms14" "b/pics/EEEC2-2/\350\256\276\350\256\2413.ms14" new file mode 100644 index 0000000..fc30f10 Binary files /dev/null and "b/pics/EEEC2-2/\350\256\276\350\256\2413.ms14" differ diff --git a/pics/EEECx/image-20241120201524763.png b/pics/EEECx/image-20241120201524763.png new file mode 100644 index 0000000..99e11d8 Binary files /dev/null and b/pics/EEECx/image-20241120201524763.png differ diff --git a/pics/EEECx/image-20241120201700281.png b/pics/EEECx/image-20241120201700281.png new file mode 100644 index 0000000..d1aa4d2 Binary files /dev/null and b/pics/EEECx/image-20241120201700281.png differ diff --git a/pics/EEECx/image-20241120202223224.png b/pics/EEECx/image-20241120202223224.png new file mode 100644 index 0000000..1183bc0 Binary files /dev/null and b/pics/EEECx/image-20241120202223224.png differ diff --git a/pics/EEECx/image-20241120202419032.png b/pics/EEECx/image-20241120202419032.png new file mode 100644 index 0000000..6b1acca Binary files /dev/null and b/pics/EEECx/image-20241120202419032.png differ diff --git a/pics/EEECx/image1.png b/pics/EEECx/image1.png new file mode 100644 index 0000000..1fcea55 Binary files /dev/null and b/pics/EEECx/image1.png differ diff --git a/pics/EEECx/image2.png b/pics/EEECx/image2.png new file mode 100644 index 0000000..e401837 Binary files /dev/null and b/pics/EEECx/image2.png differ diff --git a/pics/EEECx/image3.png b/pics/EEECx/image3.png new file mode 100644 index 0000000..31cf69c Binary files /dev/null and b/pics/EEECx/image3.png differ diff --git a/pics/EEECx/image4.png b/pics/EEECx/image4.png new file mode 100644 index 0000000..446b9d0 Binary files /dev/null and b/pics/EEECx/image4.png differ