Given a binary tree root. Split the binary tree into two subtrees by removing 1 edge such that the product of the sums of the subtrees are maximized.
Since the answer may be too large, return it modulo 10^9 + 7.
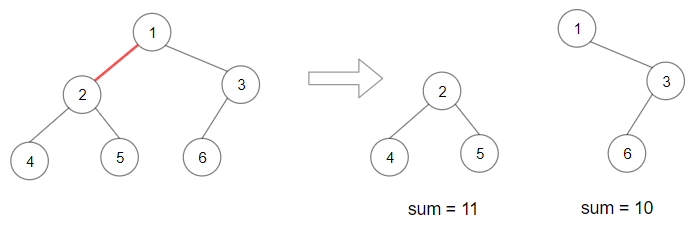
Example 1:
Input: root = [1,2,3,4,5,6] Output: 110 Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)
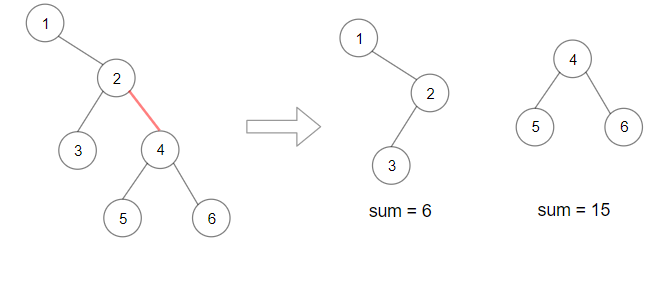
Example 2:
Input: root = [1,null,2,3,4,null,null,5,6] Output: 90 Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)
Example 3:
Input: root = [2,3,9,10,7,8,6,5,4,11,1] Output: 1025
Example 4:
Input: root = [1,1] Output: 1
Constraints:
- Each tree has at most
50000nodes and at least2nodes. - Each node's value is between
[1, 10000].