web

Quicksort

Resources:

1. visualgo - quicksort
2. Khan Academy - Quick Sort
3. Quicksort in JavaScript
4. Wikipedia Quicksort

Quadratic Sorts

So far, we've looked at sorts that take O(n²) time. Those were:

• Insertion Sort
• Bubble Sort

Both of the algorithms are helpful for learning how sorting works, but aren't actually used because they are too slow.

In this lesson, we will look a recursive sorting algorithm and understand why it is faster.

Quicksort

Simple Algorithms Practice

Write a function called partition that takes in an array and partitions it in three parts. Let the middle element of the array be called pivot. Partition the array around the pivot in three subarrays lessThanPivot, equalToPivot and greaterThanPivot. Return the subarrays in an object with properties lessThanPivot, equalToPivot, greaterThanPivot

Example

// pivot, middle element arr[3] = 10
partition([11,8,15,10,4,14,2])// => {
//                                    lessThanPivot: [8, 4, 2],
//                                    equalToPivot: [10],
//                                    greaterThanPivot: [11, 15, 14]
//                                  }

• What does it return for arr = [27, 38, 12, 39, 27, 16]?

Visualization

1)

Picking as pivot the middle element. Everything less than the pivot goes to the left and everything that is greater to the right

2)

Here's how it works:

1. If the array has only one element, return it. This is our base case.
2. Find the middle element of the array and name it pivot
3. Move all the elements smaller than the pivot into an array called lessThanPivot.
4. Move all the elements equal to the pivot into an array called equalToPivot.
5. Move all the elements greater than the pivot into an array called greaterThanPivot
6. Concatenate and recurse. Concatenate the recursive call of quickSort passing in lessThanPivot with equalToPivot and with the recursive call of quickSort passing in greaterThanPivot.

Let's go through some examples:

Example One:

Lets walk over the steps mentioned above for arr1 = [8,4,2]

• Step 1. Skip this step as arr1 has 3 elements.
• Step 2. pivot = 4
• Step 3. lessThanPivot = [2]
• Step 4. equalToPivot = [4]
• Step 5. greater = [8]
• Step 6. return concatenating quickSort([2]) + [4] + quickSort([8])

The recursive calls quickSort([2]) and quickSort([4]) hit the basecase in step one and return the input. Therefore, the function returns [2,4,8]

Example Two:

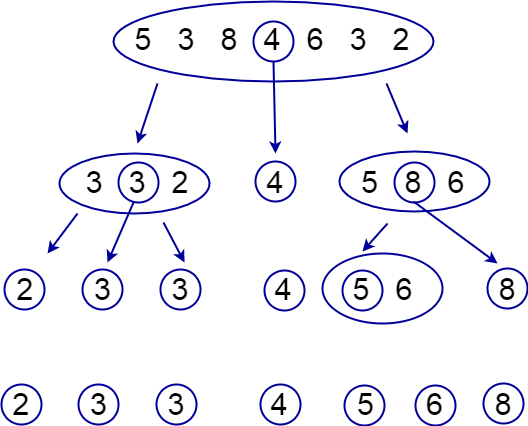
arr2 = [11,8,15,10,4,14,2]

Steps

• 1st. Skip this step as arr2 has 7 elements.
• 2nd. pivot = 10
• 3rd. lessThanPivot = [8,4,2]
• 4th. equalToPivot = [10]
• 5th. greaterThanPivot = [11,15,14]
• 6th. return concatenated quickSort([8,4,2]) + [10] + quickSort([11,15,14])

quickSort([8,4,2]) yields [2,4,8] as we saw in example one

recursive quickSort([11,15,14]) :

1. Skip this step as the array has 3 elements
2. pivot = 15
3. lessThanPivot = [11,14]
4. equalToPivot = [15]
5. greaterThanPivot = []
6. return concatenated quickSort([11,14]) + [15] + quickSort([])

recursive quickSort(11,14) :

1. Skip this step as the array has 2 elements
2. pivot = 11
3. lessThanPivot = []
4. equalToPivot = [11]
5. greaterThanPivot = [14]
6. return concatenated quickSort([]) + [11] + quickSort([14]) which yields [11,14]

Therefore, quickSort([11,15,14]) = [11,14,15]

And so quickSort([8,4,2]) + [10] + quickSort([11,15,14]) = [2,4,8,10,11,14,15]

In Code:

const quickSort = (arr) => {
  if (arr.length < 2) return arr //base case

  let middle = Math.floor(arr.length / 2)
  let pivot = arr[middle]
  let lessThanPivot = []
  let equalToPivot = []
  let greaterThanPivot = []

  for (let num of arr) {
    if (num < pivot) {
      lessThanPivot.push(num)
    } else if (num > pivot) {
      greaterThanPivot.push(num)
    } else {
      equalToPivot.push(num)
    }
  }
  console.log(arr, "with pivot:", pivot)
  console.log(`sort(${lessThanPivot}) + ${equalToPivot} + sort(${greaterThanPivot})`)

  // Concatenate the result of quick sorting lessThanPivot with equalToPivot with the result of quick sorting greaterThanPivot
  const result = quickSort(lessThanPivot).concat(equalToPivot).concat(quickSort(greaterThanPivot)) //recursive call

  console.log('result ->', result)
  console.log()
  return result
}

Time Complexity: O(n log n)

Exercises

1. Quicksort 1 - Hackerrank
2. Quicksort 2 - Hackerrank
3. Quicksort 3 - Hackerrank
4. Sort a Linked List
5. Sort Colors
6. Codewars - swapped3-7