So far, we have looked at the following ways of storing information:
- Array
- Linked List
- Stack
- Queue
- Hashmap
Today, we will look at a new data structure called a Tree
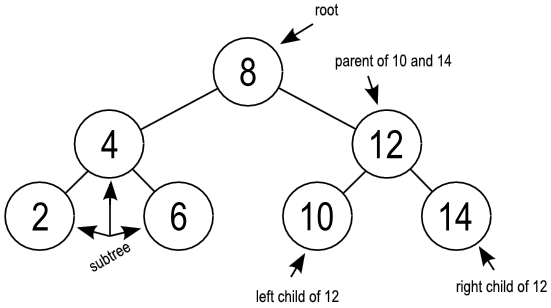
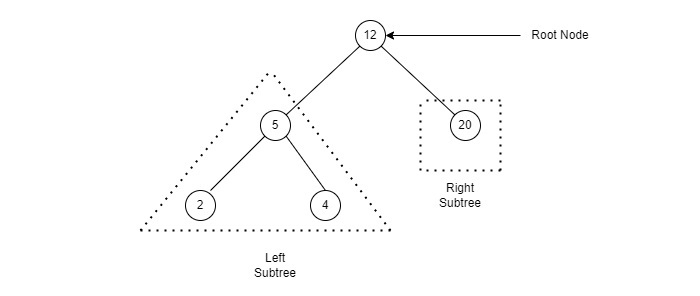
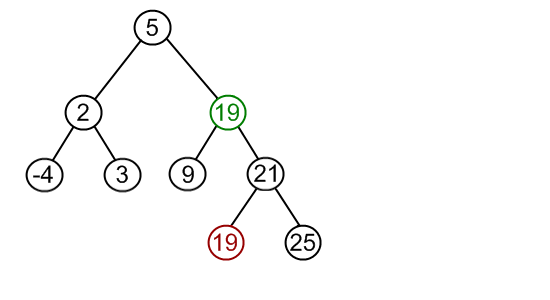
How would you model the diagram below?
This information is presented in a new way then what we have seen before. Instead of a straightforward list, there are branching possibilities. Each element is linked not only to one element, but two different possibilities. Arrays and Linked lists only operate in one dimension (a line). Hashmaps can track groupings, but don't have any order. We are looking for a structure that can represent one object being linked to multiple objects AND keeping a sequence.
Trees are comprised of nodes, and are very similar to Linked Lists. Just like a LinkedListNode, a TreeNode has a value. While a LinkedListNode has only one next Node, a TreeNode can have any number of next Nodes. The most common type of tree is called a Binary Tree where each TreeNode can have up to two next Nodes.
class TreeNode {
let val: Int
var left: TreeNode?
var right: TreeNode?
init(_ val: Int) {
self.val = val
}
}Just like a LinkedListNode might not have a next Node, a TreeNode might not have a left or a right. Before we go on to traversing a tree, let's take a look at some key terminology.
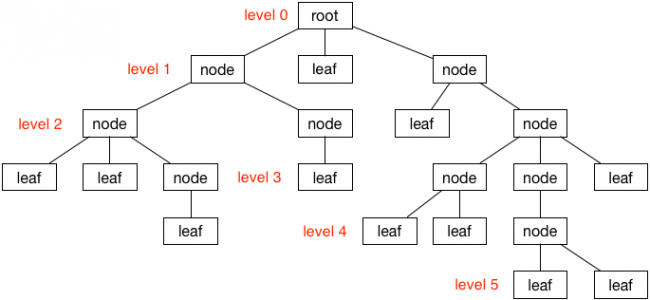
- The top of any tree is called the
root - The left and right nodes are called
children - The left and right nodes are
siblingsto each other - The node the holds the children is called the
parent - You can pick any node in a tree and call it the
rootof its own subtree. We can start to see its recursive structure. - A node at the bottom of a tree is called a
leaf - An
edgeis a line connecting two nodes - The
heightof the tree is the number of edges in the longest path from the top to the bottom - The
levelof a node is which row it is on. The root is at level 0, its children are at level 1, and so on.
With this structure, we are able to create a variety of different trees. It will be helpful to use the following terminology to define what kind of tree we are working with.
A Binary Tree is a tree where every node has 0,1 or 2 children.
Example
(source: wikipedia)
Non Example
(source: wikipedia)
A Full Binary Tree is a Binary Tree where every node has 0 or 2 children.
Example
(source: wikipedia)
Non Example
(source: wikipedia)
A Complete Binary Tree is a Binary Tree where every level except possibly the last is completely filled and each node on the last level is as far left as possible. A Complete Binary Tree is allowed to have a single Node with one child, all others must have 0 or 2.
Example
(source: wikipedia)
Non Example
(source: wikipedia)
A Balanced Binary Tree is a Binary tree where the left and right subtrees height differ by at most 1 and both the left and right tree are balanced. A balanced Binary Tree is one where the height is O(log(n)), where n is the number of elements.
Example
(source: wikipedia)
Non Example
(source: wikipedia)
A Degenerate tree is a Tree where every parent has, at most, one child. It's effectively just a Linked List.
Degenerate Tree
Source: https://secweb.cs.odu.edu/~zeil/cs361/web/website/Lectures/bst/pages/bstdegen.jpg
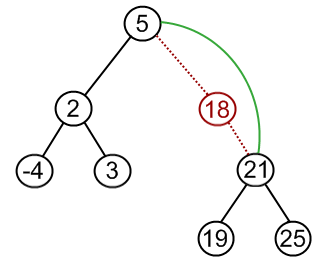
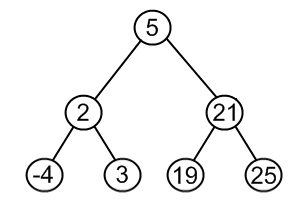
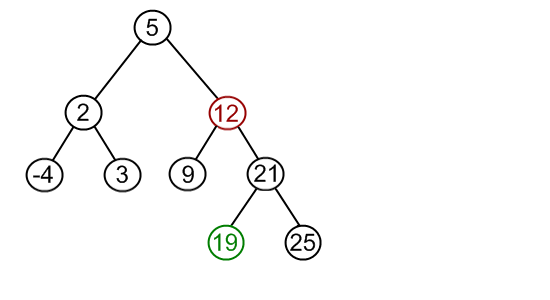
A Binary Search Tree is Binary Tree with two conditions:
- Every node in the
leftchild's subtree its parent - Every node in the
rightchild's subtree its parent - (Generally BSTs are defined to have unique values)
Example
(source: wikipedia)
Non Example
(source: wikipedia)
A Min Heap is a Complete Binary Tree where each parent is smaller than its children. The root is the smallest value in the tree
Example
(source: wikipedia)
Source: (https://www.cs.cmu.edu/~adamchik)
A Max Heap is a Complete Binary Tree where each parent is bigger than its children. The root is the biggest value in the tree.
Example
(source: wikipedia)
TreeNode class
class TreeNode {
var key: Int
var left: TreeNode?
var right: TreeNode?
init(key: Int) {
self.key = key
}
}Building a simple tree
let root = TreeNode(key: 1)
let nodeTwo = TreeNode(key: 2)
let nodeThree = TreeNode(key: 3)
let nodeFour = TreeNode(key: 4)
let nodeFive = TreeNode(key: 5)
root.left = nodeTwo
root.right = nodeThree
nodeTwo.left = nodeFour
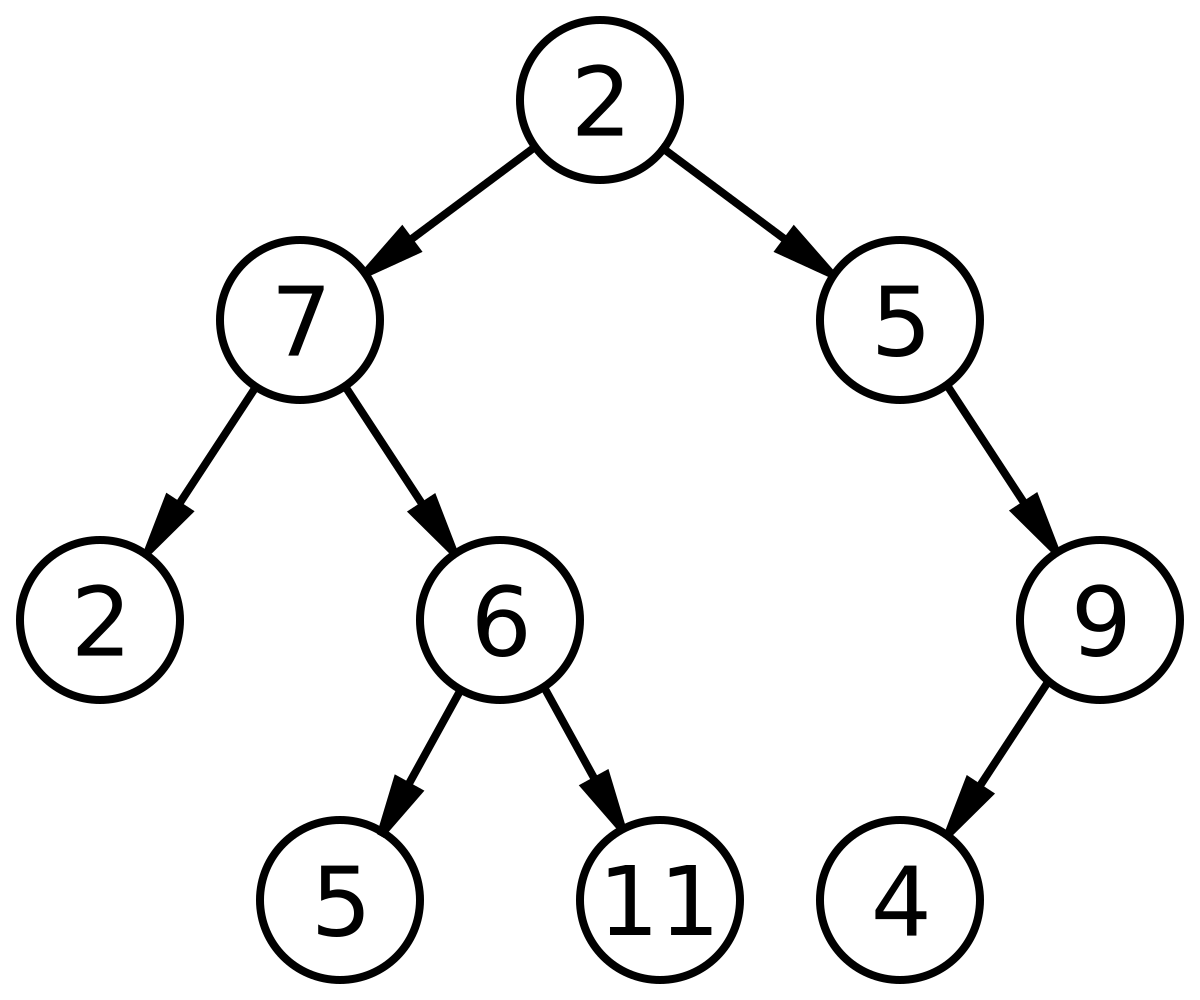
nodeTwo.right = nodeFiveWhat kind of tree is this?
A Min Heap
How can we print out all the values? Unlike an array, we can't just iterate over it. And unlike a linked list, it isn't clear which way to go next. We have two nexts and we have to go to both of them. We have two strategies for how we can look at every node.
- Look at all of the nodes on a single level before going to the next one (Breadth First Search)
- Follow a chain all the way to a leaf node before returning back to the top (Depth First Search)
We will look at each in turn.
For a Breadth First Search, we want to look at:
- All the nodes on level 0
- Then all the nodes on level 1
- Then all the nodes on level 2
Here's how we can implement this in code. First, we'll need a Queue. Here's one from a few weeks ago:
class LLNode<Key> {
let val: Key
var next: LLNode?
init(val: Key) {
self.val = val
}
}
struct Queue<T> {
private var head: LLNode<T>?
private var tail: LLNode<T>?
var isEmpty: Bool {
return head == nil
}
mutating func enQueue(_ newElement: T) {
let newNode = LLNode(val: newElement)
guard let tail = tail else {
self.head = newNode
self.tail = newNode
return
}
tail.next = newNode
self.tail = newNode
}
mutating func deQueue() -> T? {
guard let oldHead = head else {
return nil
}
self.head = oldHead.next
if oldHead.next == nil {
self.tail = nil
}
return oldHead.val
}
func peek() -> T? {
return self.head?.val
}
}Now we can implement our breadth first search
func bfs<T>(root: TreeNode<T>) {
var myQueue = Queue<TreeNode<T>>()
myQueue.enQueue(root)
while !myQueue.isEmpty {
let visitedElement = myQueue.deQueue()!
print(visitedElement.key)
if let leftChild = visitedElement.left {
myQueue.enQueue(leftChild)
}
if let rightChild = visitedElement.right {
myQueue.enQueue(rightChild)
}
}
}This algorithm visits each node on each level before proceding to the next level.
There are three ways in which we can implement a depth first search. We will see each in turn below.
func dfs<T>(root: TreeNode<T>?) {
guard let root = root else { return }
print(root.key)
dfs(root: root.left)
dfs(root: root.right)
}func dfs<T>(root: TreeNode<T>?) {
guard let root = root else { return }
dfs(root: root.left)
print(root.key)
dfs(root: root.right)
}func dfs<T>(root: TreeNode<T>?) {
guard let root = root else { return }
dfs(root: root.left)
dfs(root: root.right)
print(root.key)
}Instead of just printing each node's key, we can have a custom closure that handles it however we want:
func dfs<T>(root: TreeNode<T>?, process: (T) -> Void = {print($0)}) {
guard let root = root else { return }
process(root.key)
dfs(root: root.left, process: process)
dfs(root: root.right, process: process)
}enum BinaryTree<T> {
case empty
indirect case node(BinaryTree, T, BinaryTree)
}Further reading from raywenderlich
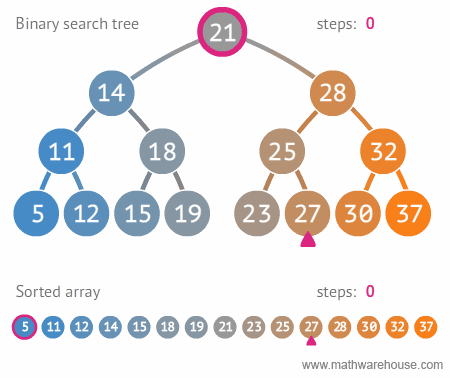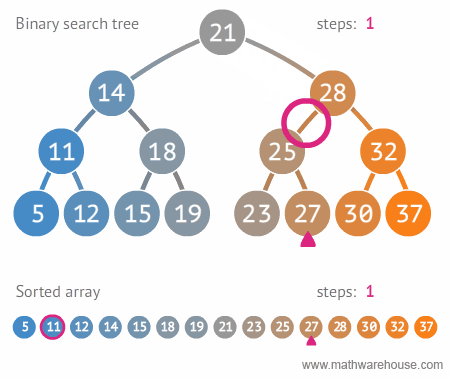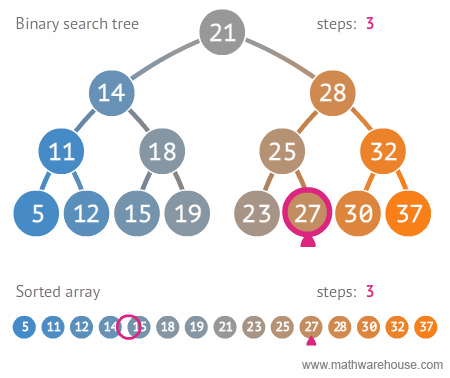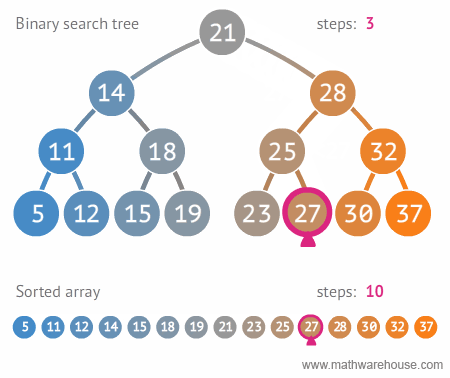
Search for 27
(Source: https://blog.penjee.com/wp-content/uploads/2015/11/binary-search-tree-sorted-array-animation.gif)
Three cases:
3. Node to be removed has two children
The worst case runtime for each of these operations is O(n). This occurs when you have a degenerate binary search tree that looks like a linked list.
Why are insertion and deletion O(1) on a linked list and O(n) for a degenerate binary search tree?
Binary Search Trees have to keep a sorted order, which means it can only insert an element in the place it belongs in the tree, which could be at the bottom.
In computer science, a tree is a widely used abstract data type (ADT)—or data structure implementing this ADT—that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.
A tree data structure can be defined recursively as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.
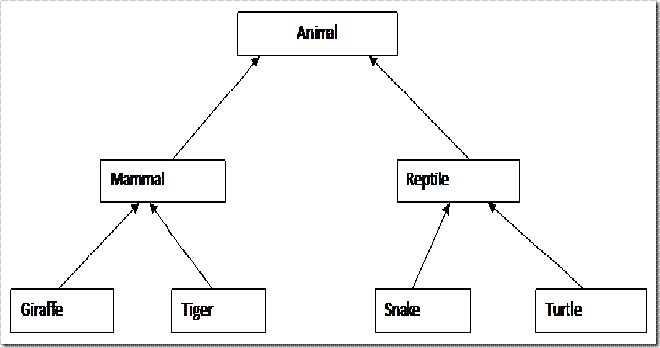
Let's implement the following hierarchical tree structure in Swift
Basic TreeNode class, doen't have the ability to add children nodes yet, let's implement this next.
class TreeNode<T> {
var value: T
var parent: TreeNode?
var children = [TreeNode]()
init(value: T) {
self.value = value
}
}Here we have added a addChild() method on the TreeNode class to have the ability to add children to the tree.
class TreeNode<T> {
var value: T
var parent: TreeNode?
var children = [TreeNode]()
init(value: T) {
self.value = value
}
public func addChild(node: TreeNode) {
children.append(node)
node.parent = self
}
}We can now add children to our animal created Tree, however when we print our animal Tree the print console does not give us a human readeable print statement as seen below. We will have to conform to CustomStringConvertible and provide implement the description variable to return a more verbose string representing our current Tree structure.
class TreeNode<T> {
var value: T
var parent: TreeNode?
var children = [TreeNode]()
init(value: T) {
self.value = value
}
public func addChild(node: TreeNode) {
children.append(node)
node.parent = self
}
}
let tree = TreeNode<String>(value: "animal")
let mammalNode = TreeNode<String>(value: "mammal")
let reptileNode = TreeNode<String>(value: "reptile")
tree.children = [mammalNode, reptileNode]
print(tree) // __lldb_expr_23.TreeNode<Swift.String>After conforming to CustomStringConvertible we can now get a more readable print statement representing the current animal Tree.
class TreeNode<T>: CustomStringConvertible {
var value: T
var parent: TreeNode?
var children = [TreeNode]()
var description: String {
guard !children.isEmpty else {
return "\(value)"
}
return "\(value)" + "{" + "\(children.map{ $0.description }.joined(separator: ", ") )" + "}"
}
init(value: T) {
self.value = value
}
public func addChild(node: TreeNode) {
children.append(node)
node.parent = self
}
}
let tree = TreeNode<String>(value: "animal")
let mammalNode = TreeNode<String>(value: "mammal")
let reptileNode = TreeNode<String>(value: "reptile")
tree.children = [mammalNode, reptileNode]
print(tree) // animal{mammal, reptile}Full Tree Implemenation including Search
class TreeNode<T: Equatable>: CustomStringConvertible {
var value: T
var parent: TreeNode?
var children = [TreeNode]()
var description: String {
guard !children.isEmpty else {
return "\(value)"
}
return "\(value)" + "{" + "\(children.map{ $0.description }.joined(separator: ", ") )" + "}"
}
init(value: T) {
self.value = value
}
public func addChild(node: TreeNode) {
children.append(node)
node.parent = self
}
public func search(value: T) -> TreeNode? {
if self.value == value {
return self
}
for child in children {
if let foundNode = child.search(value: value) {
return foundNode
}
}
return nil
}
}
let tree = TreeNode<String>(value: "animal")
let mammalNode = TreeNode<String>(value: "mammal")
let reptileNode = TreeNode<String>(value: "reptile")
let giraffeNode = TreeNode<String>(value: "giraffe")
let tigerNode = TreeNode<String>(value: "tiger")
let snakeNode = TreeNode<String>(value: "snake")
let turtleNode = TreeNode<String>(value: "turtle")
tree.children = [mammalNode, reptileNode]
mammalNode.children = [giraffeNode, tigerNode]
reptileNode.children = [snakeNode, turtleNode]
print(tree) // animal{mammal{giraffe, tiger}, reptile{snake, turtle}}The height of the Animal tree above is 2.
The depth of the reptile node is 1.
Tree - Data Structure - Wikipedia
Trees - Ray Wenderlich
Exercise - Create the following Tree, search and print the Primate Node