Skip to content

Latest commit

 

History

History
1053 lines (829 loc) · 29.1 KB

README.md

File metadata and controls

1053 lines (829 loc) · 29.1 KB
Raw

Regressão 1

Notebook

Fábio Cavaleti e Gabriela Barros

Introdução

Regressão e classificação

Regressão e classificação são tarefas de aprendizado supervisionado. A regressão é uma tarefa que tenta predizer um valor numérico e contínuo enquanto que a classificação tenta classificar o dado em uma classe que pertence a um conjunto discreto de classes.

Regressão Linear

Regressão linear é uma técnica estatística simples de regressão que tenta encontrar uma relação linear entre as variáveis explicativas e a variável resposta.

A equação a seguir descreve de maneira generalizada uma regressão linear:

$$ y = \beta_0 + \beta_1 * x_1 + \beta_2 * x_2 + ... + \beta_n * x_n + \varepsilon $$

  • $y$ é a variável resposta, ou seja, é a variável que o nosso modelo tenta prever e obter um valor.
  • $x$ são nossas variáveis explicativas que são as entradas do nosso modelo
  • Os valores de $\beta$ são os coeficientes, os quais são os parâmetros que nosso modelo procurar calcular para obter o melhor modelo possível
  • $\beta_0$ é chamado de bias e é um coeficiente que não é acompanhado de nenhuma variável explicativa. Ou melhor, podemos considerar que há uma variável $x_0 = 1$
  • Os coeficientes, junto com as variáveis explicativas, são chamados de componente sistemático do nosso modelo. Isso porque eles não são aleatórios e não variam uma vez que seus valores são determinados
  • $\varepsilon$ é o erro do nosso modelo. Nosso modelo gera um valor predito ,$\hat{y}$, que tem uma diferença do valor real da variável resposta $y$. Afinal, estamos fazendo uma aproximação e isso significa que nem sempre nosso modelo irá acertar 100% o valor correto. Podemos chamar $\varepsilon$ de componente aleatório do nosso modelo, pois, em termos estatísticos, ele se trata de uma variável aleatória
  • Como toda variável aleatória, $\varepsilon$ segue alguma distribuição de probabilidade. A regressão linear assume que o erro segue uma distribuição Normal.

Uma outra forma de representar a regressão linear é pela seguinte relação: $$ h_{\theta}(x) = \theta^Tx $$

Essa é uma representação vetorial em que $\theta$ é o vetor dos coeficientes e $x$ é o vetor das variáveis explicativas.

Gráfico Regressao Linear

Função de custo

Agora que sabemos como é a função da regressão linear, como podemos encontrar os melhores valores para os coeficientes?

  • Pensando de maneira lógica, se nós buscarmos uma maneira de minimizar o valor do erro, então a precisão de nossas predições será maximada.
  • Dessa maneira, precisamos montar uma função que nos diz o quanto nós estamos errando. Esse tipo de função é chamado de função de custo $J$.
  • Na regressão linear a maneira mais utilizada de se calcular o erro aleatório é utilizando a métrica MSE que calcula a média dos quadrados das diferenças entre os valores previstos pelo modelo e os valores reais observados.
  • Dessa forma, baseada na métrica MSE, temos a seguinte função de custo $J(\theta)$:

$$ J(\theta) = \frac{1}{2m}\sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)} )^2 $$

  • Observe, porém que nossa função $J(\theta)$ divide a fórmula do MSE por 2. Isso é opcional e pode nos ajudar nos próximos passamos como veremos adiante.

  • Agora que temos uma função de custo, minimizar essa função significa minimizar o erro e consequentemente otimizar nosso modelo.

  • Uma maneira natural de realizarmos essa minimização é calcularmos a derivada parcial para cada valor de $\theta_i$ e igualarmos todas as equações a zero e assim encontrarmos os melhores valores de cada $\theta$.

  • Esse método, entretanto, é muito custoso e tem uma complexidade de $O(N^3)$.

Gradiente Descendente

Uma maneira mais otimizada de minimizar a função de custo e obter os valores dos coeficientes é utilizando a técnica do gradiente descendente. Mas o que é isso?

O que é Gradiente ($\nabla f$)

  • A função gradiente é um conceito fundamental em cálculo vetorial e análise matemática.
  • Sem entrar em muitos detalhes matemáticos, gradiente é uma função matemática que indica a direção em que a função original cresce mais rapidamente. Ou seja ele indica o caminho em que se deve percorrer se quer maximizar uma função
  • No nosso caso, estamos interessado no negativo do gradiente ($-\nabla f$), que nos indica a direção em que a função decresce mais rapidamente. Com isso podemos resolver problemas de minimização.

Gradiente Negativo

Gradiente Descendente

  • O gradiente descendete é um método iterativo que utiliza o gradiente para minimizar uma função. Em cada interação, o gradiente descendente "caminha" uma certa quantidade na direção em que a função decresce mais rapidamente
  • Basicamente, utilizamos o valor da última iteração do algoritmo e o gradiente da função para dar um novo passo na iteração atual

$$ \theta_i = \theta_i + \alpha * \frac{\partial}{\partial\theta_i}J(\theta_i) $$

  • O passo é definido pelo hiperparâmetro chamado de taxa de aprendizado ($\alpha$). Esse hiperparâmetro é muito importante pois ele define o quanto vamos caminhar a cada interação. Se a taxa de aprendizado for muito pequena, então nosso algorítmo terá muitas iterações, várias desnecessárias, e teremos um custo computacional muito grande. Se a taxa de aprendizado for muito grande, então corremos o risco de na última iteração ultrapassarmos o ponto de mínimo da função, fazendo com que o algoritmo não consiga convergir.

taxa de aprendizado

  • O que se faz na prática é ir alterando o valor do learning rate conforme as iterações vão ocorrendo. Dessa forma, começamos com passos grandes e o tamanho dos passos vão diminuindo a cada iteração até chegarmos em um ponto de parada.

taxa de aprendizado

  • Falando um pouco sobre como calcular o gradiente... Para a métrica MSE temos que: $$ \frac{\partial MSE}{\partial\theta_i} = \frac{2}{m}\sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)} )x_i $$

  • É aqui que a divisão por 2 da nossa função $J(\theta)$ nos ajuda. Ele cancela a multiplicação por 2 e obtemos:

$$ \frac{\partial J(\theta)}{\partial\theta_i} = \frac{1}{m}\sum\limits_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)} )x_i $$

Gradiente descendente funcionando visualmente

gradiente exemplo

Observações finais

  • A técnica do gradiente descendente caminha na direção em que a função decresce mais rapidamente. Entretanto, o gradiente descendente pode estar caminhando para um ponto de mínimo local. Ou seja, ele não garante que vamos chegar até o ponto de mínimo global. Tudo depende da função e da inicialização aleatória da primeira iteração.

Interpretabilidade

  • A regressão linear é um modelo de fácil interpretabilidade. Após o treinamento do modelo podemos observar o valor dos coeficientes para verificarmos quais variáveis possuem maior impacto no cálculo da saída.

Linearidade

Como verificar linearidade?

  • Há duas formas muito comuns de testar a linearidade dos dados:
  • A primeira, e a mais simples, é basicamente fazer um plot com a variável resposta e cada uma das variáveis explicativas e verificar se há uma relação linear entre elas.
  • A segunda maneira, e a mais utilizada, é após o treinamento do modelo, observar graficamente a dispersão dos resíduos com os valores preditos pelo modelo.
  • Um resíduo é a diferença entre o valor real $y$ e o valor predito $\hat{y}$
  • O gráfico residual vs fitted é um gráfico em que no eixo $x$ temos os valores preditos pelo nosso modelo e no eixo y temos os resíduos das predições
  • Uma relação linear entre os dados indica que não deve haver relação entre os resíduos e as predições. Dessa forma, teremos linearidade se nesse gráfico os pontos estiverem uniformemente distribuídos sobre uma linha horizontal

Análise de resíduo

Linearização

  • Mas e caso não encontremos uma relação linear entre as variáveis?
  • Muitas relações são possíveis de serem linearizadas através de um transformação que pode acontecer tanto em $y$ quanto em $x$
  • Ao aplicar transformações em $y$ depois podemos apenas desfazer a transformação para obter o resultado original
  • Aplicar transformações em $x$ implica em adicionar novas features em nosso modelo com essas novas transformações e isso deve ser feito com cuidado pois acabar levando o nosso modelo ao overfitting, principalmente com features polinomiais
  • Alguns exemplos: $log(y)$, $x_2 = x_1^2$, $x_3 = x_1*x_2$

Vantagens da Regressão Linear

  • É um modelo simples e eficiente
  • Possui fácil interpretabilidade
  • Muitas coisas possuem relações lineares, e muitas outras relações podem ser linearizadas
  • Entender os fundamentos da regressão linear ajuda no entendimento de outros algortimos poderosos e complexos como o SVM e Redes Neurais.

Prática de regressão linear

# Instalando bibliotecas

# !pip install ISLP
# !pip install seaborn
#Importando bibliotecas

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from ISLP import load_data

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_diabetes
#Informações sobre o dataset em: https://islp.readthedocs.io/en/latest/datasets/Boston.html
df = load_data('Boston')
df.head()
<style scoped> .dataframe tbody tr th:only-of-type { vertical-align: middle; } 
.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}
</style>
crim zn indus chas nox rm age dis rad tax ptratio lstat medv
0 0.00632 18.0 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 4.98 24.0
1 0.02731 0.0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 9.14 21.6
2 0.02729 0.0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 4.03 34.7
3 0.03237 0.0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 2.94 33.4
4 0.06905 0.0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 5.33 36.2 
df.columns
Index(['crim', 'zn', 'indus', 'chas', 'nox', 'rm', 'age', 'dis', 'rad', 'tax',
       'ptratio', 'lstat', 'medv'],
      dtype='object')

df.shape
(506, 13)

df.describe()
<style scoped> .dataframe tbody tr th:only-of-type { vertical-align: middle; } 
.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}
</style>
crim zn indus chas nox rm age dis rad tax ptratio lstat medv
count 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000
mean 3.613524 11.363636 11.136779 0.069170 0.554695 6.284634 68.574901 3.795043 9.549407 408.237154 18.455534 12.653063 22.532806
std 8.601545 23.322453 6.860353 0.253994 0.115878 0.702617 28.148861 2.105710 8.707259 168.537116 2.164946 7.141062 9.197104
min 0.006320 0.000000 0.460000 0.000000 0.385000 3.561000 2.900000 1.129600 1.000000 187.000000 12.600000 1.730000 5.000000
25% 0.082045 0.000000 5.190000 0.000000 0.449000 5.885500 45.025000 2.100175 4.000000 279.000000 17.400000 6.950000 17.025000
50% 0.256510 0.000000 9.690000 0.000000 0.538000 6.208500 77.500000 3.207450 5.000000 330.000000 19.050000 11.360000 21.200000
75% 3.677083 12.500000 18.100000 0.000000 0.624000 6.623500 94.075000 5.188425 24.000000 666.000000 20.200000 16.955000 25.000000
max 88.976200 100.000000 27.740000 1.000000 0.871000 8.780000 100.000000 12.126500 24.000000 711.000000 22.000000 37.970000 50.000000 
# Plotting `Price` with remaining columns

plt.figure(figsize = (20, 15))
plotnumber = 1

for column in df:
    if plotnumber <= 14:
        ax = plt.subplot(3, 5, plotnumber)
        sns.scatterplot(x = df['medv'], y = df[column])
        
    plotnumber += 1

plt.tight_layout()
plt.show()

png

target = ['medv']
# features =  [x for x in df.columns if x not in target]
features = ['lstat', 'rm']
y = df[target]
X = df[features]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

model = LinearRegression()

model.fit(X_train,y_train)

y_pred = model.predict(X_test)


plt.scatter(y_test, y_pred)
plt.xlabel("Valores Reais")
plt.ylabel("Valores Previstos")
plt.title("Gráfico de Dispersão: Valores Reais vs Valores Previstos")
plt.show()

png

from sklearn import metrics

print('MAE:', metrics.mean_absolute_error(y_test, y_pred))
print('MSE:', metrics.mean_squared_error(y_test, y_pred))
print('RMSE:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
MAE: 3.898759721382358
MSE: 31.243290601783627
RMSE: 5.589569804715174

residuos = y_test - y_pred
plt.scatter(y_pred, residuos)
plt.xlabel("Valores Previstos")
plt.ylabel("Resíduos")
plt.axhline(y=0, color='r', linestyle='--')
plt.title("Gráfico de Resíduos")
plt.show()

png



# Transformar os coeficientes em uma lista unidimensional
coeficientes_unidimensional = model.coef_.flatten()

# Criar o DataFrame com os coeficientes unidimensionais
coeficientes = pd.DataFrame(coeficientes_unidimensional, columns=['Coefficients'], index=X.columns)
coeficientes



<style scoped>
    .dataframe tbody tr th:only-of-type {
        vertical-align: middle;
    }

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}


</style>


  
    

      
      Coefficients
    

  
  
    

      lstat
      -0.632499
    

    

      rm
      5.465099
    

  





model.intercept_


array([-3.84117708])



df.head()



<style scoped>
    .dataframe tbody tr th:only-of-type {
        vertical-align: middle;
    }

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}


</style>


  
    

      
      crim
      zn
      indus
      chas
      nox
      rm
      age
      dis
      rad
      tax
      ptratio
      lstat
      medv
    

  
  
    

      0
      0.00632
      18.0
      2.31
      0
      0.538
      6.575
      65.2
      4.0900
      1
      296
      15.3
      4.98
      24.0
    

    

      1
      0.02731
      0.0
      7.07
      0
      0.469
      6.421
      78.9
      4.9671
      2
      242
      17.8
      9.14
      21.6
    

    

      2
      0.02729
      0.0
      7.07
      0
      0.469
      7.185
      61.1
      4.9671
      2
      242
      17.8
      4.03
      34.7
    

    

      3
      0.03237
      0.0
      2.18
      0
      0.458
      6.998
      45.8
      6.0622
      3
      222
      18.7
      2.94
      33.4
    

    

      4
      0.06905
      0.0
      2.18
      0
      0.458
      7.147
      54.2
      6.0622
      3
      222
      18.7
      5.33
      36.2
    

  





df['medv_log'] = np.log(df['medv'])
df.drop('medv', axis = 1,inplace=True)


target = ['medv_log']
# features =  [x for x in df.columns if x not in target]
features = ['lstat', 'rm']

y = df[target]
X = df[features]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

model = LinearRegression()

model.fit(X_train,y_train)

y_pred = model.predict(X_test)


plt.scatter(y_test, y_pred)
plt.xlabel("Valores Reais")
plt.ylabel("Valores Previstos")
plt.title("Gráfico de Dispersão: Valores Reais vs Valores Previstos")
plt.show()


png


residuos = y_test - y_pred
plt.scatter(y_pred, residuos)
plt.xlabel("Valores Previstos")
plt.ylabel("Resíduos")
plt.axhline(y=0, color='r', linestyle='--')
plt.title("Gráfico de Resíduos")
plt.show()


png


results = y_test
results['y_pred'] = y_pred
results



<style scoped>
    .dataframe tbody tr th:only-of-type {
        vertical-align: middle;
    }

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}


</style>


  
    

      
      medv_log
      y_pred
    

  
  
    

      173
      3.161247
      3.188354
    

    

      274
      3.478158
      3.444702
    

    

      491
      2.610070
      2.786197
    

    

      72
      3.126761
      3.271902
    

    

      452
      2.778819
      2.860652
    

    

      ...
      ...
      ...
    

    

      412
      2.884801
      1.979498
    

    

      436
      2.261763
      2.854283
    

    

      411
      2.844909
      2.762125
    

    

      86
      3.113515
      2.987545
    

    

      75
      3.063391
      3.173820
    

  



102 rows × 2 columns




# Transformar os coeficientes em uma lista unidimensional
coeficientes_unidimensional = model.coef_.flatten()

# Criar o DataFrame com os coeficientes unidimensionais
coeficientes = pd.DataFrame(coeficientes_unidimensional, columns=['Coefficients'], index=X.columns)
coeficientes



<style scoped>
    .dataframe tbody tr th:only-of-type {
        vertical-align: middle;
    }

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}


</style>


  
    

      
      Coefficients
    

  
  
    

      lstat
      -0.037781
    

    

      rm
      0.140859
    

  





Regressão Logística


A Regressão Logística é um método estatístico que modela a probabilidade de determinado evento pertencer ou não a uma classe a partir de um conjunto de variáveis independentes. Assim, a Regressão Logística, diferente da Regressão Linear, é um algoritmo de classificação binária. A principal vantagem da regressão logística é a interpretabilidade.
Logistic Regression: Maximum Likelihood Estimation & Gradient Descent


Suposições do modelo


    

  • A variável resposta Y deve ser binária, i.e., $y_i \in {0,1}$, spam ou não spam, fraude ou não fraude;
    • 

  • Ausência de multicolineariedade: as variáveis preditoras X$ = (x_1,x_2,...,x_n)$ devem ser independentes entre si;
    • 

  • A relação entre as variáveis preditoras e a função preditora sigmóide é linear.
    • 



Comparação com a regressão linear:


Diferente da regressão linear, a regressão logística não presspõe:


    

  • homocedasticidade(variância constante);
    • 

  • normalidade dos resíduos;
    • 

  • relação linear entre variáveis preditoras e variável predita.
    • 



A função Sigmóide


A função logística ou sigmóde


A função logística é definida por:
$$f(z) = \frac{1} {1 + e^{-z}}, z \in \mathbb{R}.$$


A função Sigmóide para Regressão Logística


$$P(y = 1| \mathbf(X)) = \sigma(z) = \frac{1} {1 + e^{-z}}$$, em que $$ z =  \hat{\beta_{0}} + \hat{\beta_1}x_1 + \hat{\beta_2} x_2 + ... + \hat{\beta_n}x_n$$.


$\beta_{0},\beta_{1},...,\beta_{2}$, assim como em regressão linear, são os parâmetros, coeficiêntes ou pesos.
ou
A função sigmoide retorna um valor entre 0 e 1. Por isso, o valor retornado pode ser interpretado como a probabilidade da observação $i$ pertencer à classe de interesse(neste caso, a classe de interesse é $y=1$).


O que o algorítmo da função logística nos retorna?


Chance


A chance ($\textit{odds}$) de um evento ocorrer é definica como a probabilidade (p) do evento ocorrer divida pelo probabilidade de o evento não ocorrer (1-p):
$$odds = \frac{p}{(1-p)}.$$


Quando aplicamos a função logarítmica em ambos os lados da equação, temos o log da chance ou $\textit{log odds}$:
$$log odds = \log{\frac{p}{(1-p)}}.$$


REGRESSÃO LOGÍSTICA – ALGORITMOS DE APRENDIZADO DE MÁQUINAS


Função de custo (ou estimando os parâmetros)


Método de Máxima Verossimilhança


O Método de Máxima Verossimilhança é um método estatístico para a estimação de parâmetros de um modelo estatístico.
$$\max_{\theta} \prod_y p(y;\theta)$$


Log Verossimilhança e Log Verossimilhança Negativa


Maximizar a Máxima Verossimilhança equivale a maximizar o logarítmo da função de Máxima Verossimilhança, já que a função logarítmica é uma função monótona (ou seja, ela preserva a relação de ordem). Consequentemente, se multiplicarmos a verossimilhança por -1, obtemos a Log Verossimilhança Negativa e encontrar seu ponto de mínimo equivale a encontrar o ponto de máximo da verossimilhança.
$$NLL(y) = -{\log(p(y))}$$


$$\min_{\theta} \sum_y {-\log(p(y;\theta))}$$


A Log Verossimilhança Negativa também é chamada de $\textit{cross-entropy}$.


Log Loss


Assim, a função de custo para regressão logística é chamada de $\textit{cross-entropy} ou \texit{LogLoss}$ e é definida da forma:
$$J(\theta) = -(y \log{h_{\theta}(x)} + (1 - y) \log {(1-h_{\theta}(x)))}$$ em que $h_{\theta}(x) = \frac{1} {1 + e^{-z}}$ com $ z =  \hat{\beta_{0}} + \hat{\beta_1}x_1 + \hat{\beta_2} x_2 + ... + \hat{\beta_n}x_n = \theta^Tx$ é nossa função preditora.
Os métodos de minimizar essa função é semelhante aos utilizados para minimizar os mínimos quadrados em regressão linear- pode ser usado o algoritmo de minimização de gradiente descendente, por exemplo.


Regressão Logística Multiclasse


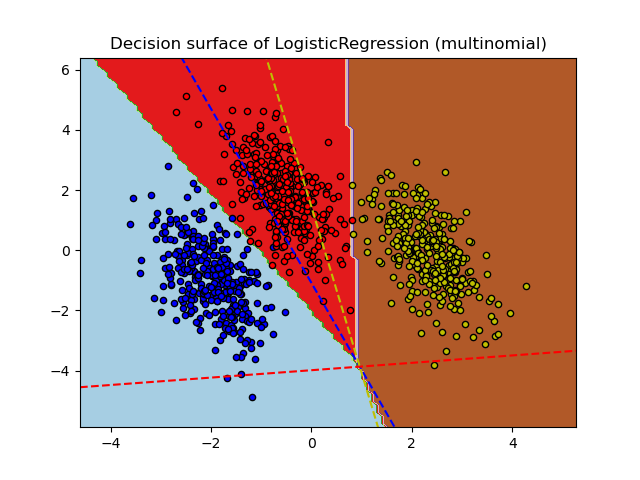
O modelo da Regressão Logística pode ser extendido para classificações de uma variável resposta em mais de duas categorias, isto é, para classificação multiclasse. Podemos usar a técnica de One-vs-All ou a Regressão Logística Multinomial:


One-vs-All (ou One-vs-Rest)


Logistic Regression: Maximum Likelihood Estimation & Gradient Descent


Regressão Logística Multinomial


Plot multinomial and One-vs-Rest Logistic Regression


Função Softmax


$$\sigma(z_i) = \frac{e^{z_{i}}}{\sum_{j=1}^K e^{z_{j}}} \ \ \ for\ i=1,2,\dots,K$$


Referências