import paradox as pd
# 定义符号,A为方程系数矩阵,x为自变量,b为常数项。
A = pd.Constant([[1, 2], [1, 3]], name='A')
x = pd.Variable([0, 0], name='x')
b = pd.Constant([3, 4], name='b')
# 使用最小二乘误差定义loss。
loss = pd.reduce_mean((A @ x - b) ** 2)
# 创建梯度下降optimizer
optimizer = pd.GradientDescentOptimizer(0.01)
# 创建loss的计算引擎,申明变量为x。
loss_engine = pd.Engine(loss, x)
# 迭代至多10000次最小化loss。
for epoch in range(10000):
optimizer.minimize(loss_engine)
loss_value = loss_engine.value()
print('loss = {:.8f}'.format(loss_value))
if loss_value < 0.0000001: # loss阈值。
break
# 输出最终结果。
print('\nx =\n{}'.format(x.value))运行结果:
...
loss = 0.00000010
loss = 0.00000010
loss = 0.00000010
x =
[ 0.99886023 1.00044064]
import numpy as np
import matplotlib.pyplot as plt
import paradox as pd
# 随机生成点的个数。
points_sum = 200
x_data = []
y_data = []
# 生成y = 2 * x + 1直线附近的随机点。
for _ in range(points_sum):
x = np.random.normal(0, 2)
y = x * 2 + 1 + np.random.normal(0, 2)
x_data.append(x)
y_data.append(y)
x_np = np.array(x_data)
y_np = np.array(y_data)
# 定义符号。
X = pd.Constant(x_np, name='x')
Y = pd.Constant(y_np, name='y')
w = pd.Variable(0, name='w')
b = pd.Variable(1, name='b')
# 使用最小二乘误差。
loss = pd.reduce_mean((w * X + b - Y) ** 2)
# 创建loss计算引擎,申明变量为w和b。
loss_engine = pd.Engine(loss, [w, b])
# 梯度下降optimizer。
optimizer = pd.GradientDescentOptimizer(0.00005)
# 迭代100次最小化loss。
for epoch in range(100):
optimizer.minimize(loss_engine)
loss_value = loss_engine.value()
print('loss = {:.8f}'.format(loss_value))
# 获取w和b的训练值。
w_value = pd.Engine(w).value()
b_value = pd.Engine(b).value()
# 绘制图像。
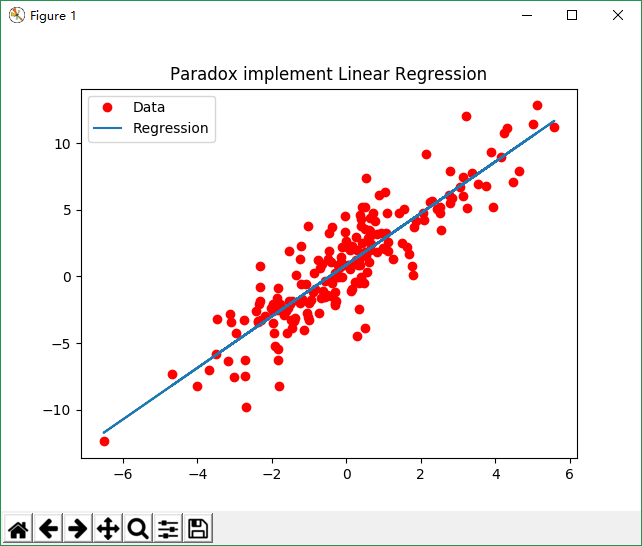
plt.title('Paradox implement Linear Regression')
plt.plot(x_data, y_data, 'ro', label='Data')
plt.plot(x_data, w_value * x_data + b_value, label='Regression')
plt.legend()
plt.show()运行结果:
import numpy as np
import matplotlib.pyplot as plt
import paradox as pd
# 每类随机生成点的个数。
points_sum = 100
c1_x = []
c1_y = []
c2_x = []
c2_y = []
# 分别在(0, 0)点附近和(8, 8)点附近生成2类随机数据。
for _ in range(points_sum):
c1_x.append(np.random.normal(0, 2))
c1_y.append(np.random.normal(0, 2))
c2_x.append(np.random.normal(8, 2))
c2_y.append(np.random.normal(8, 2))
# 定义符号。
c1 = pd.Constant([c1_x, c1_y], name='c1')
c2 = pd.Constant([c2_x, c2_y], name='c2')
W = pd.Variable([[1, 1], [1, 1]], name='w')
B = pd.Variable([[1], [1]], name='b')
# 定义SVM loss函数。
loss = pd.reduce_mean(pd.maximum(0, [[1, -1]] @ (W @ c1 + B) + 1) + pd.maximum(0, [[-1, 1]] @ (W @ c2 + B) + 1))
# 创建loss计算引擎,申明变量为W和B。
loss_engine = pd.Engine(loss, [W, B])
# 创建梯度下降optimizer。
optimizer = pd.GradientDescentOptimizer(0.01)
# 迭代至多1000次最小化loss。
for epoch in range(1000):
optimizer.minimize(loss_engine)
loss_value = loss_engine.value()
print('loss = {:.8f}'.format(loss_value))
if loss_value < 0.001: # loss阈值。
break
# 获取W和B的训练结果。
w_data = pd.Engine(W).value()
b_data = pd.Engine(B).value()
# 计算分类直线的斜率和截距。
k = (w_data[1, 0] - w_data[0, 0]) / (w_data[0, 1] - w_data[1, 1])
b = (b_data[1, 0] - b_data[0, 0]) / (w_data[0, 1] - w_data[1, 1])
# 分类面的端点。
x_range = np.array([np.min(c1_x), np.max(c2_x)])
# 绘制图像。
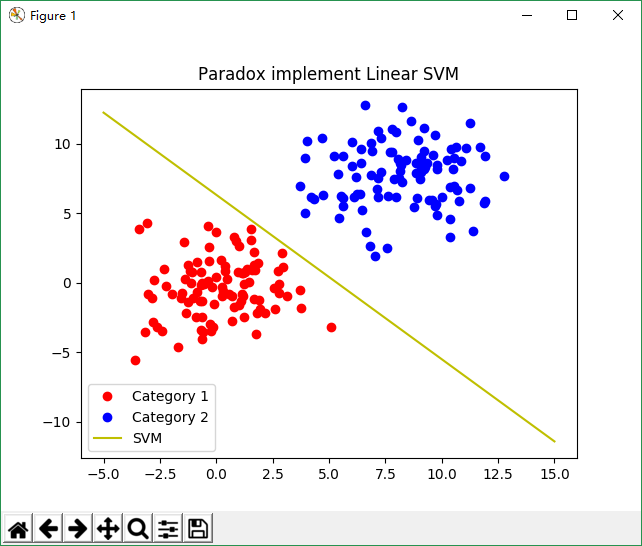
plt.title('Paradox implement Linear SVM')
plt.plot(c1_x, c1_y, 'ro', label='Category 1')
plt.plot(c2_x, c2_y, 'bo', label='Category 2')
plt.plot(x_range, k * x_range + b, 'y', label='SVM')
plt.legend()
plt.show()运行结果:
import numpy as np
import matplotlib.pyplot as plt
import paradox as pd
# 每类随机生成点的个数。
points_sum = 100
# 在(0, 0)点附近生成一堆点然后以4为半径在周围生成一堆点构成2类随机数据。
c1_x, c1_y, c2_x, c2_y = [], [], [], []
for _ in range(points_sum):
c1_x.append(np.random.normal(0, 1))
c1_y.append(np.random.normal(0, 1))
r = np.random.normal(4, 1)
theta = np.random.normal(0, 2 * np.pi)
c2_x.append(r * np.cos(theta))
c2_y.append(r * np.sin(theta))
c_x = c1_x + c2_x
c_y = c1_y + c2_y
# 定义符号。
A = pd.Variable([c_x, c_y], name='A')
W1 = pd.Variable(np.random.random((4, 2)), name='W1') # 输入层到隐含层的权重矩阵。
W2 = pd.Variable(np.random.random((2, 4)), name='W2') # 隐含层到输出层的权重矩阵。
B1 = pd.Variable(np.random.random((4, 1)), name='B1') # 隐含层的偏置。
B2 = pd.Variable(np.random.random((2, 1)), name='B2') # 输出层的偏置。
K = pd.Constant([[-1] * points_sum + [1] * points_sum, [1] * points_sum + [-1] * points_sum])
# 构建2x4x2网络,使用ReLu激活函数。
model = pd.maximum(W2 @ pd.maximum(W1 @ A + B1, 0) + B2, 0)
# 使用SVM loss。
loss = pd.reduce_mean(pd.maximum(pd.reduce_sum(K * model, axis=0) + 1, 0))
# 创建loss计算引擎,申明变量为W1,W2,B1和B2。
loss_engine = pd.Engine(loss, [W1, W2, B1, B2])
# 创建梯度下降optimizer。
optimizer = pd.GradientDescentOptimizer(0.03)
# 迭代至多10000次最小化loss。
for epoch in range(10000):
optimizer.minimize(loss_engine)
if epoch % 100 == 0: # 每100次epoch检查一次loss。
loss_value = loss_engine.value()
print('loss = {:.8f}'.format(loss_value))
if loss_value < 0.001: # loss阈值。
break
# 创建预测函数。
predict = pd.where(pd.reduce_sum([[-1], [1]] * model, axis=0) < 0, -1, 1)
# 创建预测函数计算引擎。
predict_engine = pd.Engine(predict)
# 设置网格密度为0.1。
h = 0.1
# 生成预测采样点网格。
x, y = np.meshgrid(np.arange(np.min(c_x) - 1, np.max(c_x) + 1, h), np.arange(np.min(c_y) - 1, np.max(c_y) + 1, h))
# 绑定变量值。
predict_engine.bind = {A: [x.ravel(), y.ravel()]}
# 生成采样点预测值。
z = predict_engine.value().reshape(x.shape)
# 绘制图像。
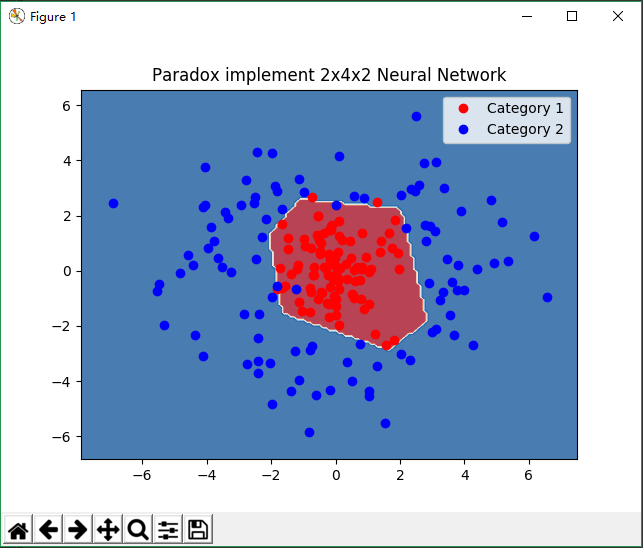
plt.title('Paradox implement 2x4x2 Neural Network')
plt.plot(c1_x, c1_y, 'ro', label='Category 1')
plt.plot(c2_x, c2_y, 'bo', label='Category 2')
plt.contourf(x, y, z, 2, cmap='RdBu', alpha=.6)
plt.legend()
plt.show()运行结果:
import numpy as np
import matplotlib.pyplot as plt
import paradox as pd
# 每类随机生成点的个数。
points_sum = 100
# 产生一个互相环绕的螺旋形数据分布。
c1_x, c1_y, c2_x, c2_y = [], [], [], []
r_step = 5 / points_sum
theta_step = 3 * np.pi / points_sum
r = 0
theta = 0
for _ in range(points_sum):
c1_x.append(r * np.cos(theta))
c1_y.append(r * np.sin(theta))
c2_x.append(-r * np.cos(theta))
c2_y.append(-r * np.sin(theta))
r += r_step
theta += theta_step
c_x = c1_x + c2_x
c_y = c1_y + c2_y
# 定义每个点的分类类别。
classification = pd.utils.generate_label_matrix([0] * points_sum + [1] * points_sum)[0]
# 定义符号。
A = pd.Variable(np.array([c_x, c_y]).transpose(), name='A')
W1 = pd.Variable(np.random.random((2, 8)), name='W1') # 输入层到隐含层的权重矩阵。
W2 = pd.Variable(np.random.random((8, 8)), name='W2') # 第1层隐含层到输出层的权重矩阵。
W3 = pd.Variable(np.random.random((8, 2)), name='W3') # 第2层隐含层到输出层的权重矩阵。
B1 = pd.Variable(np.random.random((1, 8)), name='B1') # 第1层隐含层的偏置。
B2 = pd.Variable(np.random.random((1, 8)), name='B2') # 第2层隐含层的偏置。
B3 = pd.Variable(np.random.random((1, 2)), name='B3') # 输出层的偏置。
# 构建2x8x8x2网络,使用ReLu激活函数。
model = pd.nn.relu(pd.nn.relu(pd.nn.relu(A @ W1 + B1) @ W2 + B2) @ W3 + B3)
# 使用Softmax loss。
loss = pd.nn.softmax_loss(model, pd.Constant(classification))
# 创建loss计算引擎,申明变量为W1,W2,B1和B2。
loss_engine = pd.Engine(loss, [W1, W2, W3, B1, B2, B3])
# 创建梯度下降optimizer。
optimizer = pd.GradientDescentOptimizer(0.1)
# 迭代至多10000次最小化loss。
for epoch in range(10000):
optimizer.minimize(loss_engine)
if epoch % 100 == 0: # 每100次epoch检查一次loss。
loss_value = loss_engine.value()
print('loss = {:.8f}'.format(loss_value))
if loss_value < 0.001: # loss阈值。
break
# 创建预测函数。
predict = pd.where(pd.reduce_sum([[-1, 1]] * model, axis=1) < 0, -1, 1)
# 创建预测函数计算引擎。
predict_engine = pd.Engine(predict)
# 设置网格密度为0.1。
h = 0.1
# 生成预测采样点网格。
x, y = np.meshgrid(np.arange(np.min(c_x) - 1, np.max(c_x) + 1, h), np.arange(np.min(c_y) - 1, np.max(c_y) + 1, h))
# 绑定变量值。
predict_engine.bind = {A: np.array([x.ravel(), y.ravel()]).transpose()}
# 生成采样点预测值。
z = predict_engine.value().reshape(x.shape)
# 绘制图像。
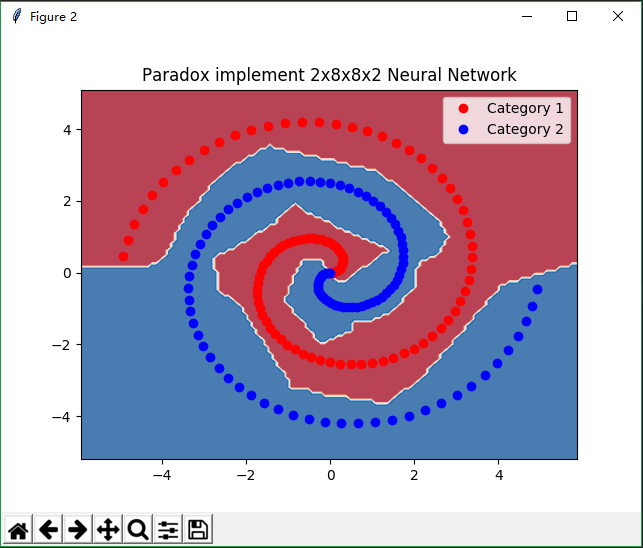
plt.title('Paradox implement 2x8x8x2 Neural Network')
plt.plot(c1_x, c1_y, 'ro', label='Category 1')
plt.plot(c2_x, c2_y, 'bo', label='Category 2')
plt.contourf(x, y, z, 2, cmap='RdBu', alpha=.6)
plt.legend()
plt.show()运行结果:
import numpy as np
import matplotlib.pyplot as plt
import paradox as pd
# 每类随机生成点的个数。
points_sum = 100
# 调用paradox的数据生成器生成三螺旋的3类数据。
data = pd.data.helical_2d(points_sum, 3, max_radius=2*np.pi)
# 组合数据。
c_x = data[0][0] + data[1][0] + data[2][0]
c_y = data[0][1] + data[1][1] + data[2][1]
# 定义每个点的分类类别。
classification = pd.utils.generate_label_matrix([0] * len(data[0][0]) + [1] * len(data[1][0]) + [2] * len(data[2][0]))[0]
# 调用高层API生成2x16x16x16x3的网络
model = pd.nn.Network()
model.add(pd.nn.Dense(16, input_dimension=2)) # 2维输入8维输出的全连接层。
model.add(pd.nn.Activation('tanh')) # 使用tanh激活函数。
model.add(pd.nn.Dense(16))
model.add(pd.nn.Activation('tanh'))
model.add(pd.nn.Dense(16))
model.add(pd.nn.Activation('tanh'))
model.add(pd.nn.Dense(3))
model.add(pd.nn.Activation('tanh'))
model.loss('softmax') # 使用softmax loss。
# 使用梯度下降优化器,使用一致性update大幅提升性能。
model.optimizer('gradient descent', rate=0.3, consistent=True)
# 执行训练。
model.train(np.array([c_x, c_y]).transpose(), classification, epochs=10000)
# 设置网格密度为0.1。
h = 0.1
# 生成预测采样点网格。
x, y = np.meshgrid(np.arange(np.min(c_x) - 1, np.max(c_x) + 1, h), np.arange(np.min(c_y) - 1, np.max(c_y) + 1, h))
# 生成采样点预测值。
z = model.predict(np.array([x.ravel(), y.ravel()]).transpose()).argmax(axis=1).reshape(x.shape)
# 绘制图像。
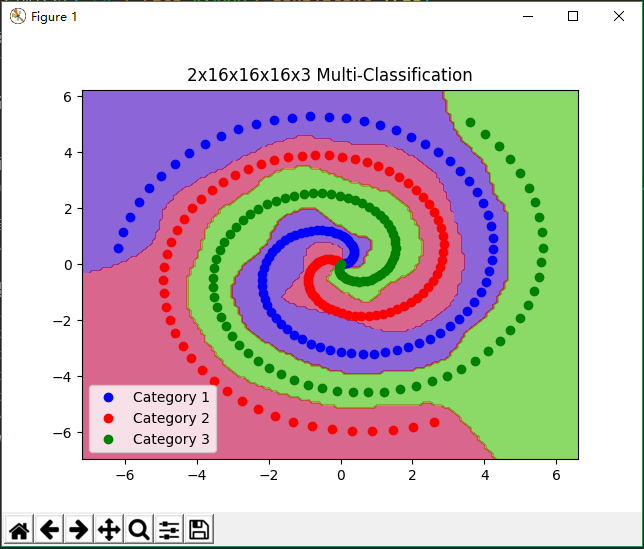
plt.title('2x16x16x16x3 Multi-Classification')
plt.plot(data[0][0], data[0][1], 'bo', label='Category 1')
plt.plot(data[1][0], data[1][1], 'ro', label='Category 2')
plt.plot(data[2][0], data[2][1], 'go', label='Category 3')
plt.contourf(x, y, z, 3, cmap='brg', alpha=.6)
plt.legend()
plt.show()运行结果:
import numpy as np
import matplotlib.pyplot as plt
import paradox as pd
# 每类随机生成点的个数。
points_sum = 50
# 调用paradox的数据生成器生成3x3网格状数据。
data = pd.data.grid_2d(points_sum, raw=3, column=3)
# 组合数据。
c_x = data[0][0] + data[1][0]
c_y = data[0][1] + data[1][1]
# 定义每个点的分类类别。
classification = pd.utils.generate_label_matrix([0] * len(data[0][0]) + [1] * len(data[1][0]))[0]
# 调用高层API生成2x8x8x8x8x2的网络,5层网络。
model = pd.nn.Network()
model.add(pd.nn.Dense(8, input_dimension=2)) # 2维输入8维输出的全连接层。
model.add(pd.nn.Activation('tanh')) # 使用tanh激活函数。
model.add(pd.nn.Dense(8))
model.add(pd.nn.Activation('tanh'))
model.add(pd.nn.Dense(8))
model.add(pd.nn.Activation('tanh'))
model.add(pd.nn.Dense(8))
model.add(pd.nn.Activation('tanh'))
model.add(pd.nn.Dense(2))
model.add(pd.nn.Activation('tanh'))
model.loss('softmax') # 使用softmax loss。
# 使用梯度下降优化器。
model.optimizer('gradient descent', rate=0.03, consistent=True)
# 执行训练。
model.train(np.array([c_x, c_y]).transpose(), classification, epochs=30000)
# 设置网格密度为0.1。
h = 0.1
# 生成预测采样点网格。
x, y = np.meshgrid(np.arange(np.min(c_x) - .1, np.max(c_x) + .1, h), np.arange(np.min(c_y) - .1, np.max(c_y) + .1, h))
# 生成采样点预测值。
z = model.predict(np.array([x.ravel(), y.ravel()]).transpose()).argmax(axis=1).reshape(x.shape)
# 绘制图像。
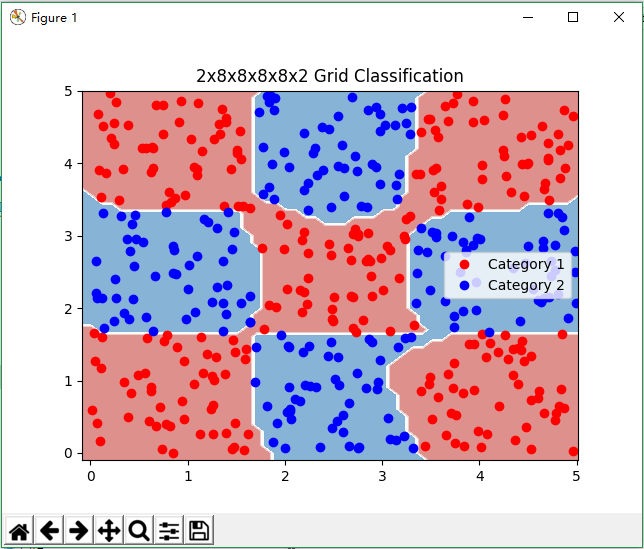
plt.title('2x8x8x8x8x2 Grid Classification')
plt.plot(data[0][0], data[0][1], 'ro', label='Category 1')
plt.plot(data[1][0], data[1][1], 'bo', label='Category 2')
plt.contourf(x, y, z, 2, cmap='RdBu', alpha=.6)
plt.legend()
plt.show()运行结果:
import os
import numpy as np
import paradox as pd
# 调用paradox的MNIST接口读取数据。
mnist_data = pd.data.MNIST('E:/mnist').read()
model_save_path = 'cnn.bin'
batch_size = 100
class AccuracyPlugin(pd.nn.Plugin): # 创建一个输出精确度和预测值的插件。
def __init__(self, data, label, index_reverse_map):
self.data = data
self.label = label
self.index_reverse_map = index_reverse_map
def end_iteration(self): # 该函数会在每次迭代完成后被调用。
predict = np.array([self.index_reverse_map[i] for i in np.array(np.argmax(self.network.predict(self.data), axis=1))])
accuracy = len(predict[predict == self.label]) / len(self.label) * 100
print('Test State [accuracy = {:.2f}%]\n{}'.format(accuracy, predict.reshape((10, 10))))
class AutoSavePlugin(pd.nn.Plugin): # 创建每个epoch结束后保存模型的插件。
def __init__(self, save_path):
self.__save_path = save_path
def end_epoch(self): # 该函数会在每个epoch结束后被调用。
pd.utils.save(model_save_path, self.network)
# 构建卷积神经网络。
if os.path.exists(model_save_path): # 如果存在保存的模型则载入,否则重新创建。
model = pd.utils.load(model_save_path)
else:
model = pd.nn.Network()
model.add(pd.cnn.Convolution2DLayer((4, 5, 5), 'valid', input_shape=(28, 28))) # 使用4个5x5的卷积核。
model.add(pd.cnn.AveragePooling2DLayer((2, 2), (2, 2))) # 2x2的均值池化。
model.add(pd.cnn.Convolution2DLayer((2, 3, 3), 'valid')) # 使用2个3x3的卷积核。
model.add(pd.cnn.MaxPooling2DLayer((2, 2), (2, 2))) # 2x2的max池化。
model.add(pd.nn.Dense(100)) # 接入100个神经元的全连接层。
model.add(pd.nn.Activation('tanh')) # tanh激活。
model.add(pd.nn.Dense(50))
model.add(pd.nn.Activation('tanh'))
model.add(pd.nn.Dense(10)) # 接入到输出0~9数字的输出层。
model.loss('softmax')
# 使用梯度下降
model.optimizer('adaptive moment estimation', rate=0.00001, decay=0.9, square_decay=0.999, consistent=True)
# 创建测试集分类数据。
lm, _, irm = pd.utils.generate_label_matrix(mnist_data['train_label'])
# 使用100张图片进行测试。
test_image = mnist_data['test_image'][:100]
test_label = mnist_data['test_label'][:100]
# 装入精度、预测值输出插件和模型保存插件。
model.add_plugin('Accuracy', AccuracyPlugin(test_image, test_label, irm))
model.add_plugin('Auto Save', AutoSavePlugin(model_save_path))
model.plugin('Training State').state_cycle = 1 # 修改Training State插件的参数为一次迭代输出一次结果。
model.regularization('l2', 0.01) # 使用L2正则化。
# 执行训练。
model.train(mnist_data['train_image'], lm, epochs=10, batch_size=batch_size)运行结果: