You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
We'll follow [1,2] and references therein (ref's to be completed) to implement the FE approximation of incompressible resistive MHD equations. As a first step we will focus on low Re & Ha numbers to avoid introducing stabilization terms. We'll follow [1] to implement mixed FE.
Following the formulation in [1], the discrete problem reads: find and such that for any and it holds
where .
Discretizing above equations with implicit Euler results in exact satisfaction of the Gauss low for every time step, this follows from [Thm 1, 1]. In [Sect. 3.4, 1] explicit Picard and Newton formulations can be found.
Tasks
Create a Julia project/driver for incompressible MHD equations.
Implement above formulation using Gridap library.
Implement Shercliff's benchmark test (See [Sec. 5.A, 2] for analytical solution).
Implement Hunt's benchmark test (See [Sec. 5.B, 2] for analytical solution).
Implement 2D island coalescence problem (a.k.a. reconnection problem?).
We'll follow [1,2] and references therein (ref's to be completed) to implement the FE approximation of incompressible resistive MHD equations. As a first step we will focus on low Re & Ha numbers to avoid introducing stabilization terms. We'll follow [1] to implement mixed FE.
Following the formulation in [1], the discrete problem reads: find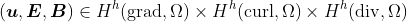 and
and 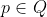 such that for any
such that for any 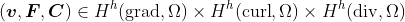 and
and 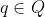 it holds
it holds
where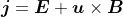 .
.
Discretizing above equations with implicit Euler results in exact satisfaction of the Gauss low for every time step, this follows from [Thm 1, 1]. In [Sect. 3.4, 1] explicit Picard and Newton formulations can be found.
Tasks
References
[1] K. Hu, Y. Ma & J. Xu Stable Finite Element Methods Preserving ∇ · B = 0 Exactly for MHD Models Numerische Mathematik, 135, 371–396 (2017)
[2] R. Planas STABILIZED FINITE ELEMENT FORMULATIONS FOR SOLVING INCOMPRESSIBLE
MAGNETOHYDRODYNAMICS PhD Thesis (2013)
The text was updated successfully, but these errors were encountered: