construct-binary-search-tree-from-preorder-traversal

Construct Binary Search Tree from Preorder Traversal

LeetCode #: 1008

Difficulty: Medium

Topics: Tree.

Problem

Return the root node of a binary search tree that matches the given preorder traversal.

(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.)

Example 1:

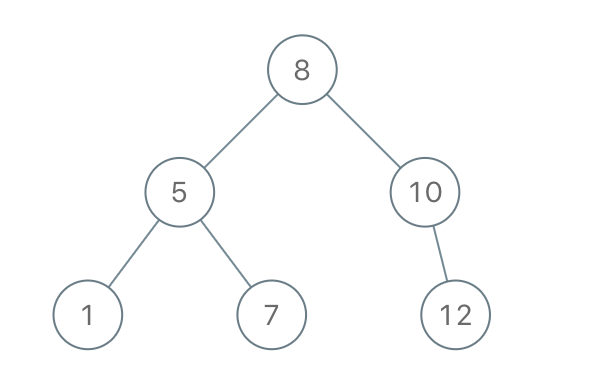
Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]

Note:

• 1 <= preorder.length <= 100
• The values of preorder are distinct.

Solution Explanation

This solution is inspired by this post written by lee215.

The main takeaway points in this solutions are:

1. Every node has an upper bound.

   • Left node is bounded by the parent node's value.
   • Right node is bounded by the ancestor's bound.
   • Using the examples above:
     • The nodes [5, 1, 7] are all bounded by 8.
     • The node 1 is bounded by 5.
     • 8 is the root node, but if you think deeper about it, it is bounded by Number.MAX_SAFE_INTEGER. i.e. imagine there is a root parent node Number.MAX_SAFE_INTEGER with left node being 8.
     • This also means that both 10 and 12 nodes, which are also right nodes, are also bounded by Number.MAX_SAFE_INTEGER.

2. We use a recursive function together with an outer index variable i to traverse and construct the tree. When we create a tree node, we increment i to process the next element in the preorder array.

3. We don't need to care about lower bound. When we construct the tree, we try to create left node first. If the condition fails (i.e. current number is greater than the parent node value), then we try to create the right node which automatically satisfies the condition, hence no lower bound is needed.

Complexity Analysis

Time complexity: O(n). We iterate through each element in preorder array only once.

Space complexity: O(h) where h is the height of the tree. Space cost is the recursive stack size.