Skip to content

Latest commit

 

History

History
240 lines (171 loc) · 7.84 KB

1203.sort-items-by-groups-respecting-dependencies.md

File metadata and controls

240 lines (171 loc) · 7.84 KB
Raw

题目地址(1203. 项目管理)

https://leetcode-cn.com/problems/sort-items-by-groups-respecting-dependencies/

题目描述


公司共有 n 个项目和  m 个小组，每个项目要不无人接手，要不就由 m 个小组之一负责。

group[i] 表示第 i 个项目所属的小组，如果这个项目目前无人接手，那么 group[i] 就等于 -1。（项目和小组都是从零开始编号的）小组可能存在没有接手任何项目的情况。

请你帮忙按要求安排这些项目的进度，并返回排序后的项目列表：

同一小组的项目，排序后在列表中彼此相邻。
项目之间存在一定的依赖关系，我们用一个列表 beforeItems 来表示，其中 beforeItems[i] 表示在进行第 i 个项目前（位于第 i 个项目左侧）应该完成的所有项目。
如果存在多个解决方案，只需要返回其中任意一个即可。如果没有合适的解决方案，就请返回一个 空列表 。

 

示例 1：


输入：n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
输出：[6,3,4,1,5,2,0,7]
示例 2：

输入：n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
输出：[]
解释：与示例 1 大致相同，但是在排序后的列表中，4 必须放在 6 的前面。
 

提示：

1 <= m <= n <= 3 * 104
group.length == beforeItems.length == n
-1 <= group[i] <= m - 1
0 <= beforeItems[i].length <= n - 1
0 <= beforeItems[i][j] <= n - 1
i != beforeItems[i][j]
beforeItems[i] 不含重复元素

前置知识

  • 图论 - 拓扑排序
  • BFS & DFS

公司

  • 暂无

思路

首先这道题不简单。 题目隐藏了三个考点，参考了其他题解之后，发现他们思路挺不错的，但讲述的并不清楚，于是写下了这篇题解。

考点一 - 如何确定拓扑排序？

对于拓扑排序，我们可以使用 BFS 和 DFS 两种方式来解决。

使用 BFS 则从入度为 0 的开始（没有任何依赖），将其邻居（依赖）逐步加入队列，并将入度（依赖数目）减去 1，如果减到 0 了，说明没啥依赖了，将其入队处理。这种做法不需要使用 visited 数组，因为环的入度不可能为 0，也就不会入队，自然不会有死循环。

代码：

    def tp_sort(self, items, indegree, neighbors):
        q = collections.deque([])
        ans = []
        for item in items:
            if not indegree[item]:
                q.append(item)
        while q:
            cur = q.popleft()
            ans.append(cur)

            for neighbor in neighbors[cur]:
                indegree[neighbor] -= 1
                if not indegree[neighbor]:
                    q.append(neighbor)

        return ans

使用 DFS 可以从图的任意一点出发，基于深度优先遍历检测是否有环。如果有，则返回 []，如果没有，则直接将 path 返回即可。使用此方法需要 visited 数组。

代码：

class Solution:
    def tp_sort(self, items: int, pres: List[List[int]]) -> List[int]:
        res = []
        visited = [0] * items
        adjacent = [[] for _ in range(items)]

        def dfs(i):
            if visited[i] == 1:
                return False
            if visited[i] == 2:
                return True
            visited[i] = 1
            for j in adjacent[i]:
                if not dfs(j):
                    return False

            visited[i] = 2
            res.append(i)
            return True
        for cur, pre in pres:
            adjacent[cur].append(pre)
        for i in range(items):
            if not dfs(i):
                return []
        return res

相关题目：

考点二 - 如何确定项目的依赖关系？

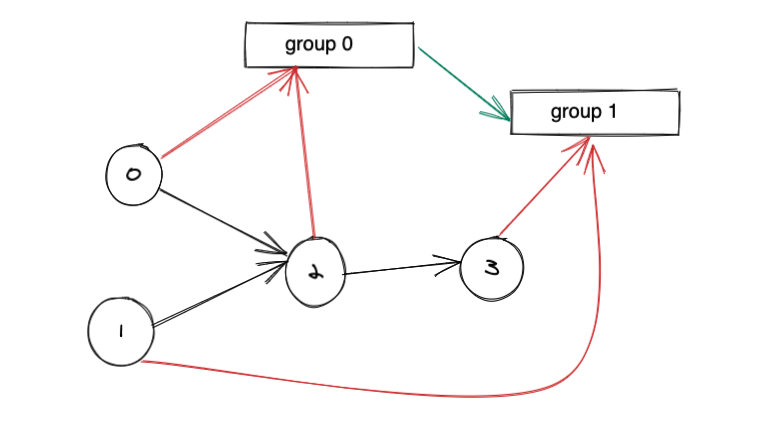
如下图：

  • 圆圈表示的是项目
  • 黑色线条表示项目的依赖关系
  • 红色线条表示项目和组之间的依赖关系
  • 绿色线条是项目之间的依赖关系

注意绿色线条不是题目给出的，而是需要我们自己生成。

生成绿色部分依赖关系的核心逻辑是如果一个项目和这个项目的依赖（如果存在）需要不同的组来完成，那么这两个组就拥有依赖关系。代码：

for pre in pres[project]:
    if group[pre] != group[project]:
        # 小组关系图
        group_indegree[group[project]] += 1
        group_neighbors[group[pre]].append(group[project])
    else:
        # 项目关系图
        # ...

pres 是题目中的 beforeItems，即项目的依赖关系。

考点三 - 无人负责的项目如何处理？

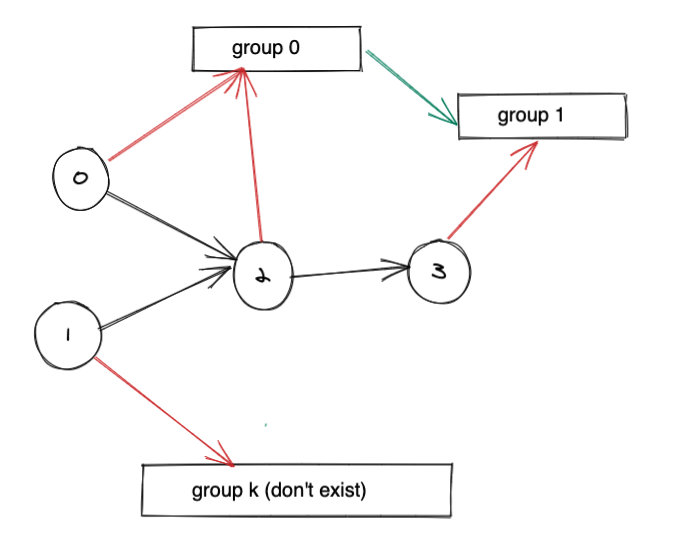
如果无组处理，意味着随便找一个组分配即可，这意味着其是图中入度为零的点。

一种方法是将这些无人处理的进行编号，只要给分别给它们一个不重复的 id 即可，注意这个 id 一定不能是已经存在的 id。由于原有的 group id 范围是 [0, m-1] 因此我们可以从 m 开始并逐个自增 1 来实现，详见代码。

代码

代码支持：Python3

Python3：

class Solution:
    def tp_sort(self, items, indegree, neighbors):
        q = collections.deque([])
        ans = []
        for item in items:
            if not indegree[item]:
                q.append(item)
        while q:
            cur = q.popleft()
            ans.append(cur)

            for neighbor in neighbors[cur]:
                indegree[neighbor] -= 1
                if not indegree[neighbor]:
                    q.append(neighbor)

        return ans

    def sortItems(self, n: int, m: int, group: List[int], pres: List[List[int]]) -> List[int]:
        max_group_id = m
        for project in range(n):
            if group[project] == -1:
                group[project] = max_group_id
                max_group_id += 1

        project_indegree = collections.defaultdict(int)
        group_indegree = collections.defaultdict(int)
        project_neighbors = collections.defaultdict(list)
        group_neighbors = collections.defaultdict(list)
        group_projects = collections.defaultdict(list)

        for project in range(n):
            group_projects[group[project]].append(project)

            for pre in pres[project]:
                if group[pre] != group[project]:
                    # 小组关系图
                    group_indegree[group[project]] += 1
                    group_neighbors[group[pre]].append(group[project])
                else:
                    # 项目关系图
                    project_indegree[project] += 1
                    project_neighbors[pre].append(project)

        ans = []

        group_queue = self.tp_sort([i for i in range(max_group_id)], group_indegree, group_neighbors)

        if len(group_queue) != max_group_id:
            return []

        for group_id in group_queue:

            project_queue = self.tp_sort(group_projects[group_id], project_indegree, project_neighbors)

            if len(project_queue) != len(group_projects[group_id]):
                return []
            ans += project_queue

        return ans

复杂度分析

令 m 和 n 分别为图的边数和顶点数。

  • 时间复杂度：$O(m + n)$
  • 空间复杂度：$O(m + n)$

大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 37K star 啦。 大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。