Skip to content

Latest commit

 

History

History
170 lines (105 loc) · 5.05 KB

Readme.md

File metadata and controls

170 lines (105 loc) · 5.05 KB
Raw

StarView

简述：关于星星的View，满足你对所有个角的星星的幻想。

描述

项目包括StarView，StarDrawable，PathStarView。

StarView由普通图片绘制而成。

StaDrawable是一个Drawable类。支持任意多个角（Angular）。

PathStarView 支持任意多个角（Angular） 的星星View。

[注] 为支持任意多个角度的星星，经过了一系列复杂的数学运算，这将在文末有说明。

预览

它们的效果如下。

000

StarView

001

StarDrawable

002

PathStarView

003

PathStarView -- depth参数

004

PathStarView -- rotate参数

006

PathStarView -- size参数

007

PathStarView -- horm参数

005

PathStarView -- 综合效果

相关算法说明

正多角星

多角星星在计算时，通过圆内接正多边形减去特定弧度的三角形而成，因此，这样的星星被我称为正多角星。

至于非正多角星。因为可以随手画出，不能归纳为数学函数。因此，不做研究。

涉及公式

涉及最多的是圆的函数公式，衍生的公式（弧的计算，三角函数等），以及勾股定理。

推导图

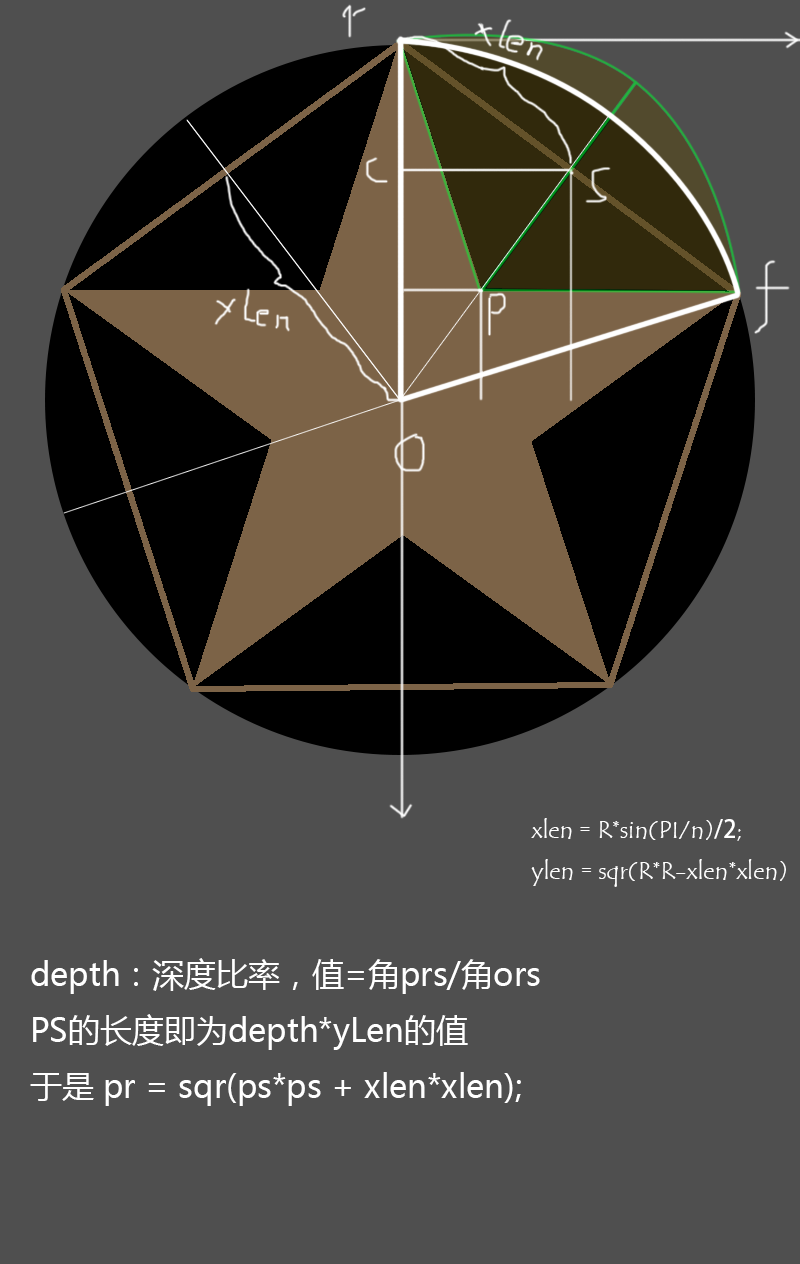
Android的屏幕坐标与常规坐标不同，其Y轴完全相反，在计算上会带来一定的困惑性。 下面是我计算正多角星的图解：

我们需要将正多角星星的每一个顶点坐标计算出来。

并且，我们需要推导出一个公用的坐标公式，这个坐标公式能够表示任意一个正多角星的顶点坐标。

代码实现

在实现过程中，我曾经通过计算出弧或三角形rpf的面积，接着通过Android的图片模式（Xfermode混合模式），循环一周，旋转固定角度相减而得到正多边形。这么做理论上行的通，实际效果则会导致存在1像素的空白线条间隙。所以，最后采用的办法是计算出所有坐标。

核心代码实现：

public class StarPathUtil {

        /**
         * 连接路径
         */
        public static Path linePath(double r,int hormCount,@FloatRange(from=0,to =1) float depth){
            Path starPath = new Path();

            double sOrs = Math.PI * (90 - 180.0 / hormCount) / 180;//角arf的弧度
            double sPro = (1.0 - depth) * sOrs;//角pra的弧度
            double sPrs = depth*sOrs;//角prs的弧度

            //圆内接正多边形边长公式2r*sin(180/n);rs = 边长/2
            double lRs = r * Math.sin(Math.PI / hormCount);
            double pr = lRs/Math.cos(sPrs);
            //p点坐标
            double pX = pr * Math.sin(sPro);
            double pY = pr * Math.cos(sPro);

            starPath.moveTo(0,0);
            /**
             * 已知圆心o（a,b）,R（x,y）,求R点顺时针移动c弧度后的坐标
             * x'=(x-a)cos(-c)-(y-b)sin(-c)+a
             * y'=(y-b)cos(-c)+(x-a)sin(-c)+b
             *
             * 此处坐标非正常坐标，为逆时针旋转，a=0,b=r,故：
             * x' = x*cos(c) - (y-r)sin(c)
             * y' = (y-r)cos(c) + x*sin(c)+r
             */
            //循环求出每旋转c==PI*(360/hormCount)/180弧度后r点和p点的坐标，并构建为路径
            for (int i = 0;i<hormCount;i++){
                double c = i*2*Math.PI/hormCount;
                double sin_c = Math.sin(c);
                double cos_c = Math.cos(c);

                //r(0,0)>>R(x,y)
                float rX2 = (float) (r*sin_c);
                float rY2 = (float) (-r*cos_c + r);
                //p(pX,pY)>>R(x,y)
                float pX2 = (float) (pX*cos_c - (pY - r)*sin_c);
                float pY2 = (float) ((pY - r)*cos_c + pX*sin_c +r);

                starPath.lineTo(rX2,rY2);
                starPath.lineTo(pX2,pY2);

                Log.e("测试","r("+rX2+","+rY2+") , p("+pX2+","+pY2+")");
            }

            starPath.close();
            Matrix m = new Matrix();
            //旋转角度
//            m.setRotate(rotate);
            //计算时坐标系平移(r,0)，现路径整体平移过去，以符合坐标系。
            m.setTranslate((float) r,0);
            starPath.transform(m);

            return starPath;
        }
    }

其他

  • 这个计算可能存在其他方式，期待能看到其他的算法实现。

  • 项目仅仅能跑而已，代码结构等还有待改进。