The Math Solver Desktop App is a Python application built using PyQt and requests libraries. This application allows users to solve mathematical problems related to solids of revolution in integrals and linear equations of first and second order by utilizing the Wolfram Alpha API.
- Solving integrals related to solids of revolution
- Solving linear equations of first and second order
- Interactive and user-friendly GUI built with PyQt
- Real-time communication with Wolfram Alpha API
- Python 3.11+
- PyQT
- requests
- Clone the repository:
git clone https://github.com/Johan-FF/Math-Assistant---Python-WolframAlpha.git
cd Math-Assistant---Python-WolframAlpha
- Create a virtual environment (optional but recommended):
python -m venv venv
source venv/bin/activate # On Windows: venv\Scripts\activate
- Install the required dependencies:
pip install -r requirements.txt
To consume WolframAlpha APIs you need to create an account on their website WolframAlpha and then create an API KEY.
Now, create a UserMath-Assistant---Python-WolframAlpha/.env file with your api key:
API_KEY='Put tour api key here...'
Ensure you have an active internet connection since the application requires access to the Wolfram Alpha API.
Run the main.py file to launch the application:
python main.py
The application's graphical interface will open, providing options to solve integrals or linear equations.
For solving integrals, enter the necessary parameters and click "Solve Integral." The application will communicate with Wolfram Alpha API and display the result.
For solving linear equations, enter the coefficients of the equations and click "Solve Equations." The application will display the solutions for the given linear equations.
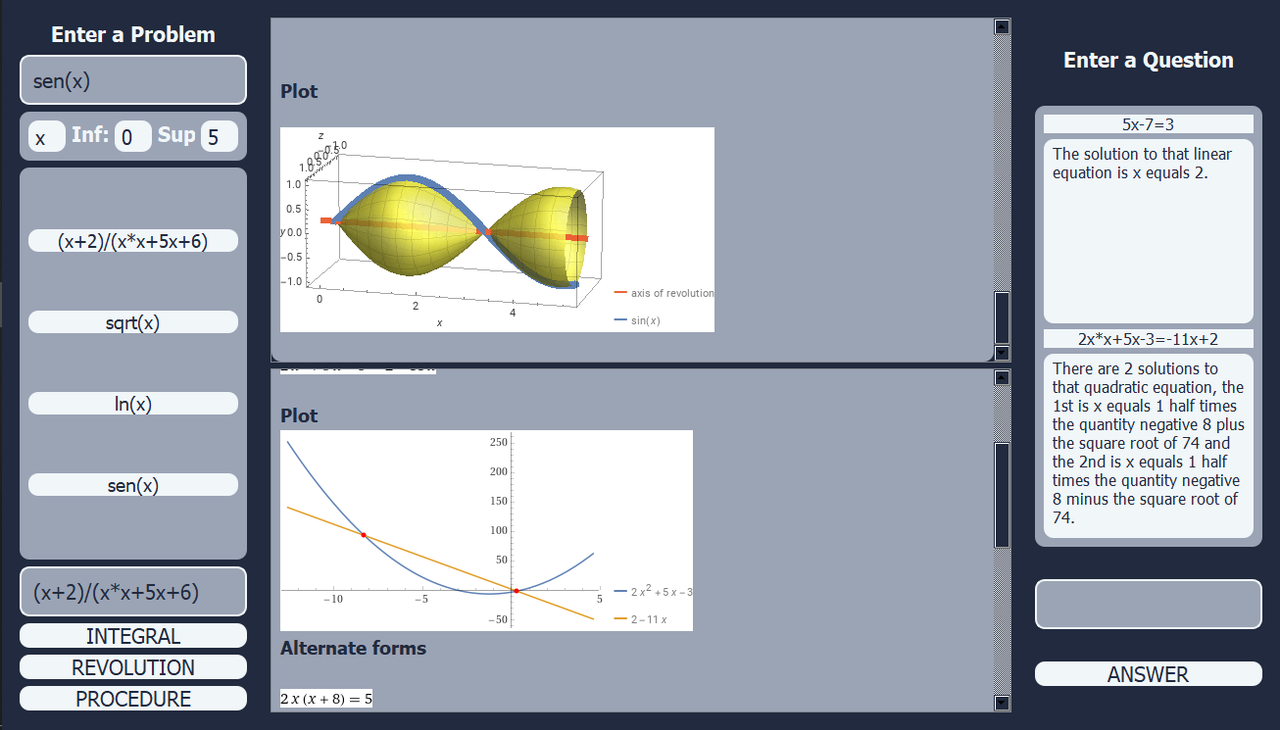
On the right side you can enter problems of low complexity, then press the "ANSWER" button. In the left part enter integrals of any type in the lower part and press the "INTEGRAL" button. In the upper part enter integrals of solids of revolution to solve with the method of disks', along with the axis on which it rotates and the limits of the integral, and press the "REVOLUTION" or "PROCEDURE" button. The middle part (vertically) of both the left and right sides serve as a query history. In the middle part (horizontally) the solution of the problem and the graph (if available) can be displayed.